7.2. Критерий q Розенбаума

Этот критерий существенно проще, чем критерий U. Он ос­нован на сравнении двух упорядоченных, но не обязательно рав­ных по численности рядов наблюдений.

Работа с критерием Розенбаума предполагает подсчет так называемых «хвостов». Потому этот критерий имеет также на­звание — «критерий хвостов». Что же такое «хвост»?

Из предыдущего критерия мы помним, что два сравниваемых ряда имеют идеальное расположение (см. 7.2), если они могут быть представлены так:

(7.5)

хххххххххххх

УУУУУУУУУУУУУУУ Поскольку в этом случае между элементами обоих рядов нет пересечений (одинаковых элементов), то между этими двумя ря­дами будет статистически значимое различие.

В том случае, если в сравниваемых рядах будут равные эле­менты, их следует размещать точно друг под другом. В этом слу­чае два сравниваемых ряда можно расположить друг под другом следующими двумя эквивалентными способами:

xxxxx|xxxxxxx| S

Т |ууyyyyy|уууууууу

(7.6)

111

(7.7)

или так:

Т |nnnnnnnn|nnnnnnn zzzzzzzz|zzzzzzzzz | S

Выбор расположения либо 7.6, либо 7.7 произволен, В обоих случаях символы T и S обозначают соответственно левый и пра­вый «хвосты». Они подсчитываются так: величина Г равна числу элементов рядов а- или г, которые находятся левее начала совпа­дающих элементов в рядах у и я; величина 5 — соответственно равна числу элементов, которые находятся в рядах у и я, правее конца совпадающих элементов.

Таким образом, величина Т «левого» хвоста в случае распо­ложения данных 7.6 равна 5, в случае 7.7 — равна 8. Величина S «правого» хвоста в случае расположения данных 7.6 равна 8, в случае 7.7 — равна 7.

Q_эмп подсчитывается очень просто — это сумма величин S и Т. Иными словами:

О_эмп= S+ Т (7.5)

После подсчета сумм "хвостов" следует обратиться к таблице 8 Приложения в соответствии с количеством испытуемых в срав­ниваемых выборках. Когда сумма Q_эмп = S + Т достаточно велика, можно считать различия сравниваемых выборок значимыми. Для более полного знакомства с критерием решим следующую задачу.

Задача 7.2. Используя тест Векслера психолог определил показатели интеллекта у двух групп учащихся из городской и сельской школы. Его интересует вопрос — будут ли обнаружены статистически значимые различия в показателях интеллекта, если в городской выборке 11 детей, а в сель­ской 12?

Решение. Для решения задачи 7.2 результаты измерений сразу представим в удобном для расчета крите­рия Q виде, т.е. расположив числа в порядке воз­растания слева направо и одно измерение под другим (верхний ряд — городская школа, ниж­ний — сельская):

112

Т |96, 100, 104, 104,120, 120,120, 120, |126, 130, 134

76,82,82,84,88,|96, 100, 102, 104, 110, 118, 120| S

В этом случае 5= 3, Т= 5, Q_эмп = S+ Т= 3 + 5 = 8

Критические значения для критерия Q находим по таблице 8 Приложения, по которой определяем, что для n1 = 11 и n2= 12 при Р= 0,05 Q_Kр = 7, а при Р = 0,01 Q_Kр = 9. В привычных обозна­чениях это выглядит следующим образом:

Q_Kр= {7 для Р<0,05

Q_Kр= {9 для Р<0,01

Соответствующая ось значимости имеет вид:

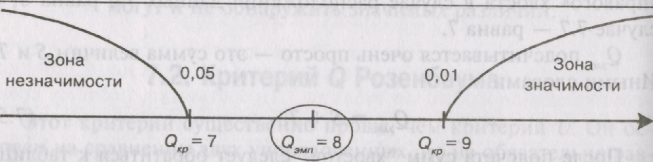
Полученное значение Q_эмп попало в зону неопределенности. Психолог поэтому может считать полученные различия между рядами значимыми на уровне 5% (т. е. принимать, что уровень интеллекта учащихся городской школы выше, чем у учащихся сельской школы) и незначимыми на уровне 1%, т.е. исходить из того, что показатели интеллекта не различаются в обеих школах. Подчеркнем еще раз, что этот выбор уровня значимости опре­деляется планом и задачами эксперимента.

В терминах статистических гипотез полученный результат мо­жет звучать так: гипотеза Я₀ — о сходстве отклоняется на уровне значимости 0,05; в этом случае принимается альтернативная ги­потеза Я, — о различии. В то же время гипотеза Я₀ — о сход­стве может приниматься на уровне значимости 0,01, в этом слу­чае альтернативная гипотеза Я, — о различии — отклоняется.

Как видим, вычисления по критерию Q существенно проще, чем по критерию U, и поэтому сравнение двух независимых вы-бхэрок, каждая из которых имеет больше 11 элементов, целесо­образно начинать именно с этого критерия. Однако критерий Q

113

менее мощный, чем критерий U. Поэтому, если критерий Q не выявляет различий, то последнее не означает, что их нет. В та­ком случае целесообразно применить другие критерии. Однако, если критерий Q выявил значимые различия на уровне 1%, то можно ограничиться только этим критерием.

Для использование критерия Q необходимо соблюдать следу­ющие условия:

1. Измерение может быть проведено в шкале порядка, интерва­лов и отношений.

2. Выборки должны быть независимыми.

3. В каждой из выборок должно быть не меньше 11 испытуемых.

4. Приведенная в настоящем пособии таблица ограничивает вер­хний предел выборки 26 испытуемыми.

5. При числе наблюдений п\ и и2 > 26 можно пользоваться следу­ющими величинами Q_Kр:

Q_Kр ={8 для Р<0,05 Q_Kр ={10 для /><0,01

6. Принципиальным условием, дающим возможность применять критерий, является наличие «хвостов», т.е. расположение дан­ных в сравниваемых рядах по типу 7.6 и 7.7. В случае располо­жения выборок следующим образом:

хххххххххххххххххххххххх

УУУУУУУУУУУУУУ

критерий Q оказывается неприменим. Следует использовать кри­терий U.

7.3. Н — критерий Крускала—Уоллиса

Критерий Я применяется для оценки различий по степени выраженности анализируемого признака одновременно между тремя, четырьмя и более выборками. Он позволяет выявить сте­пень изменения признака в выборках, не указывая, однако, на направление этих изменений.

114

Критерий основан на том принципе, что чем меньше взаи­мопересечение выборок, тем выше уровень значимости H_эмп Сле­дует подчеркнуть, что в выборках может быть разное количество испытуемых, хотя в приведенных ниже задачах приводится рав­ное число испытуемых в выборках.

Работа с данными начинается с того, что все выборки услов­но объединяются по порядку встречающихся величин в одну вы­борку и значениям этой объединенной выборки проставляются ранги. Затем полученные ранги проставляются исходным выбо­рочным данным и по каждой выборке отдельно подсчитывается сумма рангов. Критерий построен на следующей идее — если различия между выборками незначимы, то и суммы рангов не будут существенно отличаться одна от другой и наоборот.

Задача 7.3. Четыре группы испытуемых выполняли тест Бурдона в разных экспериментальных условиях. Задача в том, чтобы установить — зависит ли эффективность выполнения теста от условий или, иными словами, существуют ли статистически достоверные различия в успешности выполне­ния теста между группами. В каждую группу вхо­дило четыре испытуемых.

Решение. Число ошибок показателя переключаемости внимания в процентах дано в таблице 7.5:

Таблица 7.5

№ испыту­емых п/п	1 группа	2 группа	3 группа	4 группа
1	23	45	34	21
2	20	12	24	22
3	34	34	25	26
4	35	11	40	27
Суммы	112	102	123	96

Для дальнейшей работы с критерием необходимо выстроить все полученные значения в один столбец по порядку и проста­вить им ранги:

115

Таблица 7.6

Данные	Ранги	Данные	Ранги
11	1	26	9
12	2	27	10
20	3	34	12
21	4	34	12
22	5	34	12
23	6	35	14
24	7	40	15
25	8	45	16
Сумма рангов 136

Проверим правильность ранжирования. Общая сумма рангов

равна 136, и по формуле (1.1) она также составляет,

следовательно, ранги проставлены правильно.

Следующий этап в подсчете Н_эмп состоит в распределении дан­ных вновь на исходные группы, но уже с полученными рангами:

Таблица 7.7

№ испы­туемых п/п	1 группа	Ранги	2 группа	Ранги	3 группа	Ранги	4 группа	Ранги
1	23	6	45	16	34	12	21	4
2	20	3	12	2	24	7	22	5
3	34	12	34	12	25	8	26	9
4	35	14	11	1	40	15	27	10
Суммы	112	35	102	31	123	42	96	28

Теперь можно подсчитать величину Н_эмп по формуле:

116

Где N — общее число членов в обобщенной выборке; n_i - число членов в каждой отдельной выборке; R²_i - квадраты сумм рангов по каждой i-ой выборке. Подставляем данные таблицы 7.7 в формулу 7.6 и получаем:

При определении критических значений критерия Н приме­нительно к четырем и более выборкам используют таблицу 12 Приложения для критерия хи-квадрат, подсчитав предварительно число степеней свободы v для с = 4. Тогда v = с — 1=4— 1 = 3. Находим по таблице 12 Приложения Н_кр и представляем в при­вычном виде:

Н_кр =7,815 для Р<0,05

Н_кр =1,345 дляР<0,01

Соответствующая «ось значимости» имеет вид:

Полученное эмпирическое значение Н_эмп оказалось суще­ственно меньше критического значения для 5% уровня. Следова­тельно, можно утверждать, что различий по показателю пере­ключаемое™ внимания между группами нет.

Переформулируем полученный результат в терминах нуле­вой и альтернативной гипотез: поскольку между показателями, измеренными в четырех разных условиях, существуют лишь случайные различия, то принимается нулевая гипотеза Н₀ т.е. гипотеза о сходстве. Иными словами, различные условия про­ведения теста Бурдона не влияют на показатели переключаемо-сти внимания.

117

Подчеркнем, что если использовать критерии, позволяющие сравнивать только два ряда значений, то полученный выше ре­зультат потребовал бы шести сравнений -- первая выборка со второй, третьей и т.д.

Для более полного знакомства с критерием Я решим задачу 7.4.

Задача 7.4. Анализируя результаты задачи 7.3, психолог об­ратил внимание, ч го наименьшей суммарной величиной рангов обладает последняя выборка испытуемых. Предположив, что данные этой вы­борки повлияли на полученный результат, он исключил данные четвертой группы из расчетов и проверил наличие различий только между пер­выми тремя группами.

Решение. Представим исходные данные сразу в виде таб­лицы 7.8:

Таблица 7.8

№ испытуемых п/п	1 группа	2 группа	3 группа
1	23	45	34
2	20	12	24
3	34	34	25
4	35	1 1	40
Суммы	112	102	123

Объединим все данные в один столбец и проставим им ранги:

Таблица 7.9

Данные	Ранги	Данные	Ранги
11	1	34	8
12	2	34	8
20	3	34	8
23	4	35	10
24	5	40	11
25	6	41	12
Сумма рангов 78

118

Подсчитаем правильность ранжирования: сумма рангов из таблицы 7.9 равна 78. По формуле (l.l) сумма рангов равняется

12х13:2 = 78 , таким образом, суммы рангов совпадают и можно

утверждать, что ранги проставлены правильно.

Снова разобьем обобщенный ряд на исходные группы, но уже с рангами и сделаем это в таблице 7.10:

Таблица 7.10

№ испы­туемых п/п	1 группа	Ранги	2 группа	Ранги	3 группа	Ранги
1	23	4	45	12	34	8
2	20	3	12	2	24	5
3	34	8	34	8	25	6
4	35	10	11	1	40	11
Суммы	112	25	102	23	123	30

Теперь можно подсчитать величину Н_эмп по формуле (7.6). Подсчет дает следующее:

В тех случаях, когда сравниваются три выборки по критерию Я, критические величины этого критерия находятся по табли­це 9 Приложения. В задаче 7.4. соответствующее значение Н_кр, для выборки размером п1 = 4, п2 = 4 и «3 = 4 составляют 5,68 для Р= 0,05 и 7,59 для Р=0,01. Используя принятый вариант запи­си, получаем выражение:

Н_кр=5,68 для Р<0,05

Н_кр= 7,59 для Р<0,01

Соответствующая «ось значимости» в этом случае имеет вид:

119

Следовательно, полученные различия по тесту Бурдона, но теперь уже между тремя группами вновь незначимы. Иными сло­вами, четвертая группа не оказала значимого влияния на общий результат. В терминах статистических гипотез: мы вновь должны принять гипотезу Н₍₎ — об отсутствии различий и отклонить ги­потезу Н₁

Для использование критерия H необходимо соблюдать следу­ющие условия:

1. Измерение должно быть проведено в шкале порядка, интерва­лов или отношений.

2. Выборки должны быть незалисимыми.

3. Допускается разное число испытуемых в сопоставляемых вы­борках.

4. При сопоставлении трех выборок допускается, чтобы в одной из них было п = 3, а в двух других п — 2. Однако в таком слу­чае различия могут быть зафиксированы лишь на 5% уровне значимости.

5. Таблица 9 Приложения предусмотрена только для трех вы­борок и {n1, п2, n3), < 5, то есть максимальное число ис­пытуемых 13О всех трех выборках может быть меньше и рав­но 5.

6. При большем числе выборок и разном количестве испытуемых в каждой выборке следует пользоваться таблицей 12 Прило­жения для критерия jcw-квадрат. В этом случае число степеней свободы при этом определяется по формуле: v = с- 1, где с -количество сопоставляемых выборок.

120

7.4. S — критерий тенденций Джонкира

Этот критерий ориентирован на выявление тенденций изме­нения измеряемого признака при сопоставлении от трех и до шести выборок. В отличие от предыдущего критерия Н, количе-ство элементов в каждой выборке должно быть одинаковым. Если же число элементов в каждой выборке различно, то необходимо случайным образом уравнять выборки, при этом неизбежно утрачивается часть информации. Если же потеря информации по-кажется слишком расточительной, то следует воспользоваться вышеприведенным критерием Н — Крускала—Уоллиса, хотя в этом случае нельзя будет выдвигать гипотезу о наличии или от­сутствии искомых тенденций.

Критерий 5 основан на следующем принципе: все выборки располагаются слева направо в порядке возрастания значений исследуемого признака. При этом выборка, в которой среднее значение или сумма всех значений меньше, чем в остальных вы­борках, располагается слева, а выборка, в которой эти же зна-чения выше, располагается правее и так далее.

После такого упорядочивания для каждого отдельного эле­мента, стоящего слева в выборке, подсчитывается число инвер­сий по отношению ко всем элементам упорядоченных выборок, расположенных правее. Инверсией для данного элемента выбор­ки считается число элементов, которые превышают данный элемент по величине по всем выборкам справа. Инверсии по отно­шению к собственной выборке, т.е. той, в которой находится данный элемент, не подсчитываются. В соответствии с этим пра­вилом у последнего столбца выборки инверсии также не подсчи­тываются, т.к. справа больше нет данных.

Правило подсчета инверсий позволяет утверждать, что чем выше величина инверсий у крайних правых столбцов, тем выше уровень значимости статистики S.

С помощью этого критерия вновь обратимся к решению-зада­чи 7.3. Но, поскольку критерий S выявляет тенденции, перефор­мулируем условие задачи.

Задача 7.4. Необходимо установить: наблюдается ли тенден­ция к увеличению ошибок при выполнении тес­та Бурдона разными испытуемыми в зависимос­ти от условий его выполнения?

121

Решение. Вновь воспроизведем таблицу 7.5, но уже как таблицу 7.11:

Таблица 7.11

№ испыту­емых п/п	1 группа	2 группа	3 группа	4 группа
1	23	45	34	21
2	20	12	24	22
3	34	34	25	26
4	35	11	40	27
Суммы	112	102	123	96

Следующий этап работы отражен в таблице 7.12. В ней данные таблицы 7.11 переструктурированы и упорядочены в соответ­ствии с возрастанием сумм исходных данных:

Таблица 7.12

№ испыту­емых п/п	1 группа	2 группа	3 группа	4 группа
1	21	45	23	34
2	22	12	20	24
3	26	34	34	25
4	27	11	35	40
Суммы	96	102	112	123

Следующий этап связан с подсчетом инверсий. Для того что­бы удобнее было подсчитывать инверсии, произведем упорядо­чение величин от наименьшего к наибольшему, но уже внутри каждой группы сверху вниз. Получится таблица 7.13:

Таблица 7.13

1 группа	2 группа	3 группа	4 группа
21	11	20	24
22	12	23	25
26	34	34	34
27	45	35	40

122

Обратим внимание на то, что в таблице 7.13 отсутствует пер­вый столбец с номерами испытуемых, поскольку порядок распо­ложения испытуемых в каждой группе перемешан.

Собственно, для подсчета инверсий можно использовать и таблицу 7.13, но мы будем считать инверсии в таблице 7.14. Ин­версии подсчитываются следующим образом: из таблицы 7.13 видно, что первое число первого столбца равняется 21. Оно срав­нивается со всеми числами остальных столбцов. Видим, что чис­ло 21 меньше следующих чисел второго, третьего и четвертого столбцов: 34, 45, 23, 34, 35, 24, 25, 34, 40. Этих чисел 9, следо­вательно, количество инверсий для числа 21 равно 9. Это число и ставим в скобках рядом с числом 21 в таблице 7.14.

Второе число в первом столбце таблицы 7.13 — 22. Оно мень­ше следующих чисел второго, третьего и четвертого столбцов: 34, 45, 23, 34, 35, 24, 25, 34, 40. Этих чисел 9 — следовательно, число инверсий для числа 22 также 9. Это число и ставим в скоб­ках рядом с числом 22, уже в таблице 7.14. И т.д. В последней, четвертой группе инверсий нет, поскольку последний столбец, по правилам подсчета критерия не с чем сравнивать.

Таблица 7.14

1 группа	2 группа	3 группа	4 группа
21 (9)	11 (8)	20(4)	24
22(9)	12(8)	23(4)	25
26(6)	34(2)	34(1)	34
27(6)	45(0)	35 (1)	40
(30)	(18)	(10)

Следующий этап — подсчет общей суммы получившихся ин- версий. Это число обозначается как А. В нашем примере оно рав­но А = 30 + 18 + 10 = 58.

Величина S_эмп критерия вычисляется по формуле:

S_эмп= 2 · А - В (7.7)

В формуле (7.7) символ В также представляет собой выраже­ние:

123

где п — количество элементов в столбце (группе) с — количество столбцов (групп) Подставляем в эти формулы необходимые данные, получаем

По соответствующим значениям (и — число испытуемых) п = 4 и (с — число групп, столбцов) с = 4 по таблице 10 Прило­жения находим величины S_Kp. В привычной записи они таковы:

S_Kp ={38 для Р< 0,05 S_Kp ={50 для Р< 0,01 Строим «ось значимости»:

Согласно полученному результату S_эмп попало в зону незначи­мости, следовательно, принимается гипотеза Н₀ о том, что тен­денция к увеличению числа ошибок в тесте Бурдона в-зависимо­сти от условий его выполнения, не выявлена. ',

Для использования критерия S необходимо соблюдать следую­щие условия:

1. Измерение может быть проведено в шкале порядка, интерва­лов и отношений.

2. Выборки должны быть независимыми.

3. Количество элементов в каждой выборке должно быть одина­ковым. Если это не так, то необходимо случайным образом уравнять выборки.

124

4. Нижняя граница применимости критерия: не менее трех выбо­рок и не менее двух элементов в каждом наблюдении. Верхняя граница определяется таблицей 10 Приложения — не более 6 выборок и не более 10 элементов в каждой выборке. Во всех других случаях следует пользоваться критерием Н.

125