7.1.2. Второй способ расчета по критерию u

Преимущество второго способа подсчета по критерию U наи­более отчетливо проявляется в тех случаях, когда две или боль­шее количество одинаковых величин будут входить в оба сравни­ваемых ряда. Поскольку в таких случаях нет определенного пра­вила расстановки одинаковых чисел, то возможна следующая си­туация, представленная в таблицах 7.2 и 7.3. В этом случае оди­наковые числа равные 25 встречаются в обоих столбцах.

Таблица 7.2

№ 1	№ 2	№3	№ 4
Группа X	Группа Y	Инверсии X/Y	Инверсии Y/X
6	-	0	._
-	8	-	1
25	-	1	—
25	-	1	_
25	-	1	_
—	25	-	4
-	25	-	4
-	25	-	4
Сумма		3	13

Таблица 7.3

№ 1	№ 2	№ 3	№4
Группа X	Группа Y	Инверсии X/Y	Инверсии Y/X
6	-	0	__
-	8	-	1
—	25	-	1
—	25	-	1

107

Продолжение таблицы 7.3
—	25	-	1
25	-	4	-
25	-	4	-
25	-	4	-
Сумма		12	4

Мы отчетливо видим, что суммы инверсий в обоих столбцах различны и зависят от того, как расположены одинаковые числа. Подчеркнем, что расположение одинаковых чисел в обоих стол­бцах правильное. В подобных случаях следует пользоваться для расчета вторым, более сложным способом. Но есть возможность производить расчет и первым способом. Для этого следует распо­лагать эти числа равномерно друг под другом, например, так:

Ряд X

-

25

-

25

-

25

-

Ряд Y

-

-

25

-

25

-

25

В условиях той же задачи (7.1) несколько изменим экспери­ментальные данные таким образом, чтобы в обоих выборках имелись одинаковые значения. Представим эти измененные дан­ные в виде таблицы 7.4.

Таблица 7.4

№ 1	№ 2	№ 3	№ 4
Группа с дополнительной мотивацией	Группа без дополнительной мотивации	Ранги X	Ранги Y
Х(n1 =8)	Y(n2 = 9)	R(x)	R(У)
6	-	1	—
—	8	-	2
25	-	(3) 3,5	—

108

	Продолжение таблицы 7.4
25	-	(4) 3,5	_
30	-	(5) 5,5	-
—	30	-	(6) 5,5
—	32	—	7
38	-	8	_
41	-	(9) 10,5	_
-	41	-	(10) 10,5
-	41	-	(11) 10,5
41	-	(12) 10,5	_
44	-	13	_
—	45	-	14
—	46	-	15
-	50	-	16
-	55	—	17
Суммы рангов		55,5	97,5

Исходные данные 7.4 располагаются так же, как и в табли­це 7.1. Затем в двух столбцах проставляются ранги, так, как буд­то бы оба столбца образуют собой один упорядоченный ряд чи­сел. Подчеркнем, однако, что ранги для чисел первого столбца помещаются в третий столбец, а ранги чисел второго столбца -в четвертый. По каждому столбцу в отдельности подсчитываются суммы рангов.

Следующим этапом, как обычно при ранжировании, являет­ся проверка его правильности. Для этого:

1. Подсчитывается общая сумма рангов из таблицы 7.4:

55,5 + 97,5 = 153

2. Рассчитывается сумма рангов по формуле (1.1):

Поскольку расчетные суммы случаев совпали, то ранжирова­ние было проведено правильно.

109

3. Затем находится наибольшая по величине ранговая сумма. Она

обозначается как R . В нашем случае она равна 97,5.

4. U_эмп вычисляется по следующей формуле: (7.4)

Где п1 — численное значение первой выборки,

п2 — численное значение второй выборки,

R_mах — наибольшая по величине сумма рангов,

п_х — количество испытуемых в группе с большей суммой рангов.

Подсчитываем величину U_эмп по формуле 7.4.

Величины критических значений уже найдены нами при рас­чете первым способом по таблице 7 Приложения, поэтому сразу строим «ось значимости», которая имеет следующий вид:

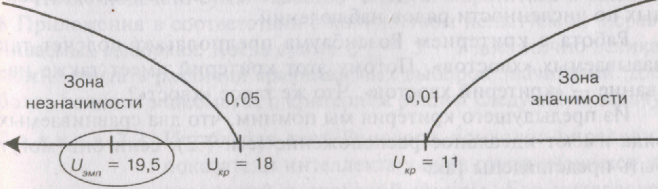
Несмотря на то что мы немножко «подправили» эксперимен­тальные данные для получения одинаковых чисел в обоих столб­цах, рассчитанное значение U_эмп вновь попало в зону незначимо­сти, следовательно принимается гипотеза Н₀ о сходстве. Тем са­мым психолог может утверждать, что мотивация не приводит к статистически значимому увеличению эффективности времени решения технической задачи.

Для применения критерия U необходимо соблюдать следую­щие условия:

1. Измерение должно быть проведено в шкале интервалов и от­ношений.

110

2. Выборки должны быть несвязанными.

3. Нижняя граница применимости критерия п1 >3 и n2 > 3 или n =2, а n2>5.

4. Верхняя граница применимости критерия: п1 и л2<60.

Замечание. Критерий U применяют и для связных выборок, рас­сматривая их при этом как независимые. Последнее возможно, если связи внутри генеральной совокуп­ности оказываются слабыми, а различия между дву­мя связными выборкам -- сильными. В этом случае возможно получение значимых различий по крите­рию U, в то время как критерии, специально пред­назначенные для связанных выборок (см. главу 6), могут и не обнаружить значимых различий.