6.2.4. Критерий Пейджа

Критерий Пейджа (его полное название L критерий тенден­ций Пейджа) можно рассматривать как эквивалент критерия Фридмана для сопоставления показателей измеренных в трех и более условиях на одной и той же"выборке испытуемых. Однако этот критерий не только позволяет выявить различия, но указы­вает на направление в изменении величин признака. Именно по­этому он является более предпочтительным.

Так, например, критерий Пейджа позволяет проверить пред­положения,о временной или ситуативно обусловленной динами­ке изменения каких-либо признаков. К сожалению, применение этого достаточно мощного критерия ограничено объемом выбор­ки — число испытуемых не может быть больше 12 и числом из­мерений признака — оно не может быть больше 6.

Задача 6.6. Решим еще раз задачу 6.5, но уже помощью кри­терия Пейджа, используя уже готовую табли­цу 6.10. При этом основной тенденцией данного примера будем считать увеличение времени ре­шения второго и четвертого заданий по сравне­нию с первым и третьим заданиями.

90

Решение. Подчеркнем, что первые несколько операций аналогичны операциям критерия Фридмана. По­этому их описание мы опускаем и отсылаем к предыдущему критерию.

Дальнейшая работа с критерием Пейджа заключается в пре­образовании таблицы 6.10. Следует попарно переставить столб­цы таблицы 6.10, ориентируясь на величины сумм рангов так, чтобы в начале таблицы стояли столбцы с наименьшей суммой рангов, а в конце таблицы — с наибольшей. Понятно, что стол­бцы с соответствующими измерениями также переставляются После проведения необходимых перестановок получается таб­лица 6. П.

Таблица 6.11

№ 1	№ 2	№ 3	№ 4	№ 5	№ 6	№ 7	№ 8	№ 9
N° испы­туе- мых п/п	Время реше- ния пер­вого зада- ния теста в сек.	Ранги вре- мени реше­ния пер- вого зада- ния теста	Время реше- ния тре­тьего зада- ния теста в сек.	Ранги вре- мени реше­ния тре- тьего зада- ния теста	Время реше- ния чет­верто- го зада- ния теста в сек.	Ранги вре- мени реше­ния чет- верто- го за- дания теста	Время реше- ния второ- го за- дания теста в сек.	Ранги вре- мени реше­ния второ- го за- дания
1	8	3	5	2	12	4	3	1
2	4	1	12	2	13	3	15	4
3	6	1	15	2	20	3	23	4
4	3	1	6	2,5	12	4	6	2,5
5	7	2	3	1	8	3	12	4
6	15	3	12	2	7	1 -	24	4
Сумма рангов		11		11,5		18		19,5

Теперь все готово для подсчета эмпирического значения критерия Пейджа. Оно определяется по формуле:

91

где R -- сумма рангов i -того столбца в упорядоченной

таблице i - порядковый номер столбца, получившийся в новой

таблице, упорядоченной по сумме рангов. с - число измерений.

Используя формулу (6.2) вычисляем эмпирическое значение L_эмп для нашего примера:

L_эмп = (11 • 1) +(11,5-2)+ (18-3)+ (19,5-4) = 166

По таблице 5 Приложения определяем критические значения L_Kр для числа испытуемых п = 6 и для числа измерений с = 4. От­метим, что в таблице критических значений критерия Пейджа до­бавлен уровень значимости 0,001 или 0,1%. Представим соответ­ствующий блок таблицы 5 Приложения в виде таблицы 6.12.

Таблица 6.12

№ — число испытуемых 6	С — количество измерений 4	Р — уровень значимости Р
	172	0,001
	167	0,01
	163	0,05

Используя привычную форму записи для критических вели­чин, получаем следующее выражение:

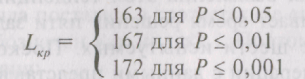
Строим «ось значимости»:

92

В нашем примере значение l_эмп попало в зону неопределен­ности, следовательно, можно считать, что тенденция увеличе­ния времени решения заданий теста №№ 2 и 4 по сравнению с заданиями №№ 1 и 3 оказалась значимой на уровне 5%.

Переформулируем полученный результат в терминах нулевой и альтернативной гипотез: поскольку между показателями, из­меренными при решении четырех заданий теста, существуют не случайные различия на 5% уровне значимости, то нулевая гипо­теза Н₀, т.е. гипотеза о сходстве отвергается, и принимается аль­тернативная гипотеза Н₁ о наличии различий.

Сравнивая выводы, полученные при решении задачи 5 с по­мощью критериев Фридмана и Пейджа, можно подумать, что они не согласуются друг с другом. Однако это не совсем так. Эти критерии обращаются к разным сторонам анализируемого мате­риала, характеризуя различные аспекты обрабатываемых данных. Если первый критерий — Фридмана — выявляет наличие разли­чий в измеренных показателях (признаках), то критерий Пейджа позволяет выявить тенденцию в изменениях величин измеряемых признаков.

Приведем еще один пример использования критерия Пейджа.

Задача 6.7. Психолог высказывает предположение о нали­чии следующей тенденции: время решения зада­ний теста будет возрастать по мере увеличения их сложности.

Решение. Для выявления этой тенденции психолог срав­нивает время решения пяти заданий теста у тех же шести испытуемых. Поскольку начальные операции с данными представлены выше, то ре­зультаты обработки по критерию Пейджа сразу представим в виде таблицы 6.13.

Как всегда необходимо проверить правильность ранжирования. Общая сумма рангов составила: 11 +22+ 11,5 +19 + 26,5 = 90

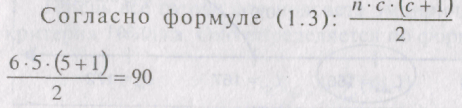она должна быть

93

Таблица 6.13

№ испы- туе- мых п/п	Время реше­ния пер- вого зада- ния теста в сек.	Ранги вре­мени реше- ния пер- вого зада- ния теста	Время реше- ния второ- го за- дания теста в сек.	Ранги вре­мени реше- ния второ- го за- дания теста	Время реше­ния тре- тьего зада- ния теста в сек.	Ранги вре­мени реше- ния тре- тьего зада- ния теста	Время реше­ния чет- верто- го зада- ния теста в сек.	Ранги вре­мени реше- ния чет- верто- го за- дания теста	Время реше- ния пято го за- дания в сек.	Ранги вре­мени реше- ния пятого зада- ния теста
1	8	3	3	1	5	2	12	4	24	5
2	4	1	15	4	12	2	13	3	35	5
3	6	1	23	5	15	2	20	4	18	3
4	3	1	6	2,5	6	2,5	12	4	43	5
5	7	2	12	4,5	3	1	8	3	12	4,5
6	15	3	24	5	12	2	7	1	22	4
Сумма рангов		11		22		11,5		18		26,5

Сравнив результаты первого и второго подсчета рангов, де­лаем вывод о том, что ранжирование произведено правильно.

Теперь, чтобы подсчитать l_эмп no формуле (6.2), не будем строить новую таблицу, а применим второй способ вычислений. Для этого рассмотрим сумму рангов как обычный ряд чисел и проранжируем этот ряд. Причем каждой величине этого нового, упорядоченного ряда поставим в соответствие его ранг. Этот ранг в формуле (6.2) обозначен как индекс /. Поэтому получатся сле­дующие соответствия:

Теперь, имея суммы рангов и соответствующие им индексы, можно применить формулу (6.2):

l_эмп = (11• 1) + (11,5 -2) + (19-3) + (22 -4) + (26,5 -5) = 311,5

Следующим этапом, как всегда, является нахождение крити­ческих величин для соответствующего числа испытуемых и изме­рений.

94

По таблице 5 Приложения находим для п = 6 и с = 5:

{291 для Р< 0,05

L_кр={299 для Р < 0,01

{307 для Р< 0,001

Строим соответственно «ось значимости»:

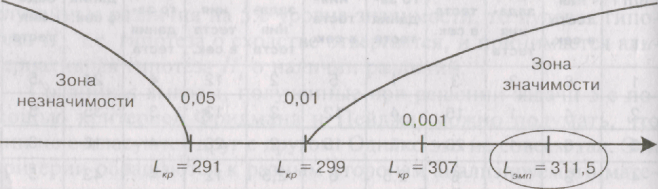
Полученная величина L_эмп критерия тенденций Пейджа ока­залась значимой на 0,1% уровне. Следовательно, по мере увели­чения сложности заданий, увеличивается и время их решения.

В терминах статистических гипотез полученный результат та­ков: Н₀ — нулевая гипотеза о сходстве должна быть отвергнута, а на уровне 0,1% следует принять альтернативную гипотезу Н₁ о наличии различий. Иными словами, тенденция увеличения вре­мени решения заданий теста с увеличением их сложности не яв­ляется случайной.

Для применения критерия Пейджа необходимо соблюдать следующие условия:

1. Измерение может быть проведено в ранговой, интервальном и в шкале отношений.

2. Выборка должна быть связной.

3. В выборке должно быть не менее двух и не больше 12 испытуе-

мых, каждый из которых имеет не менее трех измеренных по-

казателей.

4 Применение критерия ограничено, так как таблицы критичсс-

ких значений рассчитаны на небольшую выборку (п < 12) и

маленькое число измерений (не больше 6). Если эти ограни-

чения не выполняются, приходится использовать критерий

Фридмана.

95