6.2.3. Критерий Фридмана

87

Приложения для критерия хи-квадрат. В этом случае число степеней свободы определяется по формуле v = с - 1, где с -количество условий измерения. (Подробнее о критерии хи-квадрат см. ниже глава 8).

С целью более глубокого овладения критерием Фридмана рассмотрим еще один вариант задачи, но уже для первых четы­рех заданий теста.

Задача 6.5. Анализируя результаты предшествующей работы с критерием Фридмана психолог предположил, что время решения четвертого задания будет значимо отличаться от времени решения первых трех заданий.

Решение. Результаты всех четырех измерений приведены в таблице 6.10, в которой произведено ранжирова­ние всех измерений по строкам и суммирование рангов по столбцам.

Таблица 6.10

№ 1	№ 2	№ 3	№ 4	№ 5	№ 6	№ 7	№ 8	№ 9
№ испы­туе- мых п/п	Время реше­ния пер­вого зада­ния теста в сек.	Ранги вре­мени реше­ния пер­вого зада- ния теста	Время реше- ния второ- го за­дания теста в сек.	Ранги вре­мени реше­ния второ­го за- дания теста	Время реше­ния тре­тьего зада­ния теста в сек.	Ранги вре­мени реше­ния тре­тьего зада- ния теста	Время реше­ния чет­верто- го зада- ния теста в сек.	Ранги вре­мени реше­ния чет­верто- го за- дания теста
1	8	3	3	1	5	2	12	4
2	4	1	15	4	12	2	13	3
3	6	1	23	4	15	2	20	3
4	3	1	6	2,5	6	2,5	12	4
5	7	2	12	4	3	1	8	3
6	15	3	24	4	12	2	7	1
Сумма рангов		1 1		19,5		11,5		18

88

Опускаем объяснения ряда операций, которые даны выше и! проверим только правильность ранжирования. Как следует из табли­цы 6.10 общая сумма рангов составила: 1 1 4- 19,5 + 1 1,5 + 18 = 60.

Согласно расчетной формуле (1.3):

она должна быть

Равенство полученных сумм подтвердило правильность ран­жирования.

Определяем эмпирическое значение критерия по формуле (6.1).

Поскольку в данном примере рассматривается четыре изме­рения, а количество испытуемых больше 4, то критические ве­личины находятся по таблице 12 Приложения для критерия хи-квадрат. Число степеней свободы определяется по формуле v = с - 1 или v = 4 - 1 = 3. Используя привычную форму записи для критических величин, получаем следующее выражение:

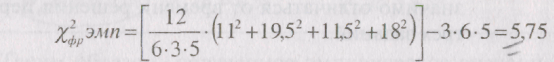
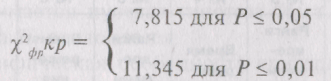
«Ось значимости» в этом случае имеет вид:

И вновь полученное эмпирическое значение критерия Фрид­мана попало в зону незначимости. Следовательно второе предпо­ложение психолога не подтвердилось, или, иначе, в терминах статистических гипотез — вновь принимается гипотеза Я₀ о сход­стве времени решения первых четырех заданий теста.

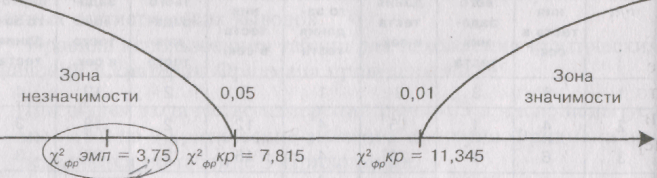
89

Для применения критерия Фридмана необходимо выполнять следующие условия:

1. Измерение должно быть проведено в шкале интервалов или отношений.

2. Выборка должна быть связной.

3. В выборке должно быть не менее двух испытуемых, каждый из которых имеет не менее трех измеренных показателей. Верх­ний предел для количества испытуемых не определен, а ко­личество измерений не может превышать 100 (см. таблицу 12 Приложения).

4. В зависимости от числа измерений и количества испытуемых используются разные таблицы значимости (правила выбора таблиц см. выше).