4.4. Разброс выборки

Разброс (иногда эту величину называют размахом) выборки обозначается буквой R. Это самый простой показатель, который можно получить для выборки — разность между максимальной и минимальной величинами данного конкретного вариационного ряда, т.е.

R = X - X

тaх тiт

Понятно, что чем сильнее варьирует измеряемый признак, тем больше величина R, и наоборот.

Однако может случиться так, что у двух выборочных рядов и средние, и размах совпадают, однако характер варьирования этих рядов будет различный. Например, даны две выборки:

X = 10 15 20 25 30 35 40 45 50 = 30 R = 40

Y = 10 28 28 30 30 30 32 32 50 = 30 R = 40

При равенстве средних и разбросов для этих двух выборочных рядов характер их варьирования различен. Для того чтобы более четко представлять характер варьирования выборок, следует об­ратиться к их распределениям.

4.5. Дисперсия

Рассмотрим еще одну очень важную числовую характеристи­ку выборки, называемую дисперсией. Дисперсия представляет со­бой наиболее часто использующуюся меру рассеяния случайной величины (переменной). Дисперсия это среднее арифметическое квадратов отклонений значений переменной от её среднего зна­чения.

49

(4.4)

где п — объем выборки

i— индекс суммирования

- среднее, вычисляемое по формуле (4.1).

Вычислим дисперсию следующего ряда

2 4 6 8 10 (4.5)

Прежде всего найдем среднее ряда (4.5). Оно равно X = 6.

Рассмотрим величины: (X_j — X) для каждого элемента ряда. Иными словами, из каждого элемента ряда 4.5 вычтем величину среднего этого ряда. Полученные величины характеризуют то, насколько каждый элемент отклоняется от средней величины в данном ряду. Обозначим полученную совокупность разностей как множество Т. Тогда Г есть:

T = (2 - 6 = -4; 4 - 6 = -2; 6 - 6 = 0; 8 - 6 = 2; 10 - 6 = 4).

Так образуется новый ряд чисел. Его особенность в том, что при сложении этих чисел обязательно получится ноль. Прове­рим: (-4) + (-2) + 0 + 2 + 4 = 0.

Отметим, что сумма такого ряда ∑(Xi — ) всегда будет равна нулю.

Для того чтобы избавиться от нуля, каждое значение разно­сти (Xi — ) возводят в квадрат, все их суммируют и затем делят на число элементов, т.е. применяют формулу 4.4. В нашем приме­ре получится следующее:

= (-4) (-4)+(-2)-(-2)+ = 16 + 4 + 0 + 4 + 16 = 40

Это и есть искомая дисперсия.

Общий алгоритм вычисления дисперсии для одной выборки следующий:

50

1. Вычисляется среднее по выборке.

2. Для каждого элемента выборки вычисляется его отклонение от

средней, т.е. получается множество Т.

3. Каждый элемент множества T возводят в квадрат.

4. Находится сумма этих квадратов.

5. Эта сумма, как и в случае вычисления среднего, делится на общее количество членов ряда — я. В ряде случаев, особенно когда величина выбоки мала, деление осуществляется не на величину п, а на величину п — 1.

Величина, получающаяся после пятого шага, и есть искомая дисперсия.

Расчет дисперсии для таблицы чисел осуществляется по фор­муле 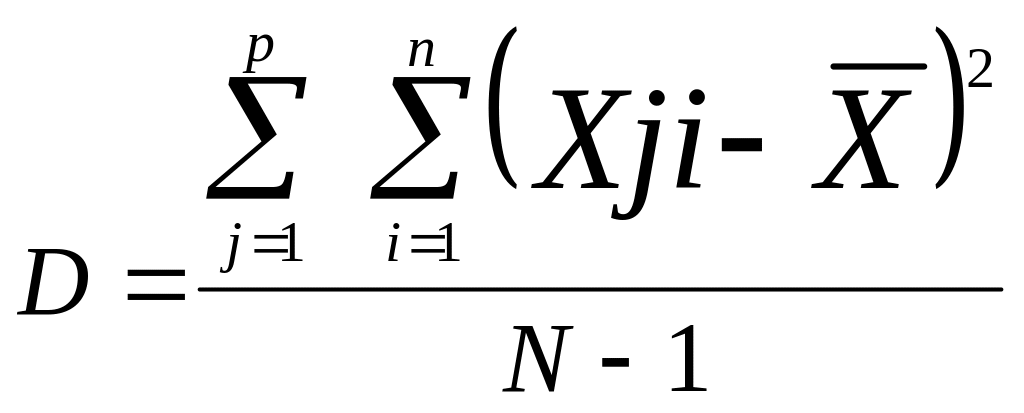4.6:

(4.6)

где х_у — значения всех переменых, полученных в эксперименте, или все элементы таблицы;

индексу меняется от 1 до p, где р число столбцов в таб­лице, а индекс i меняется от 1 до п, где п — число ис­пытуемых или число строк в таблице.

—общая средняя всех элементов таблицы, вычисленная по формуле 4.3;

N — общее число всех элементов в таблице (анализируемой совокупности экспериментальных данных) и в общем случае N = р -п.

Дисперсию для генеральной совокупности принято обозна­чать как σ², а дисперсию выборки как , причем индекс х обо­значает, что дисперсия характеризует варьирование числовых значений признака вокруг их средней арифметической.

Преимущество дисперсии перед размахом в том, что диспер­сию можно представить как сумму ряда чисел (согласно ее оп-

51

ределению), т.е. разложить на составные компоненты, позволяя тем самым более подробно охарактеризовать исходную выборку. Важная характеристика дисперсии заключается также и в том, что с её помощью можно сравнивать выборки, различные по объему.

Однако сама дисперсия, как характеристика отклонения от среднего, часто неудобна для интерпретации. Так, например, предположим, что в эксперименте измерялся рост в сантимет­рах, тогда размерность дисперсии будет являться характеристи­кой площади, а не линейного размера (поскольку при подсчете дисперсии сантиметр возводится в квадрат).

Для того чтобы приблизить размерность дисперсии к размер­ности измеряемого признака применяют операцию извлечения квадратного корня из дисперсии. Полученную величину называ­ют стандартным отклонением.

Из суммы квадратов, деленных на число членов ряда извле­кается квадратный корень.

(4.7)

Другими словами, стандартное отклонение выборки Sx пред­ставляет собой корень квадратный, извлеченный из дисперсии

выборки . Стандартное отклонение для генеральной совокуп­ности обозначают также символом а. Подчеркнем еще раз, что размерность стандартного отклонения и размерность исходного ряда совпадают.

В нашем примере