Формулы для определения главного вектора и главного момента в декартовой системе координат

Модуль главного вектора

, (5)

где

, , (6)

(R_x, R_y, R_z — проекции главного вектора на соответствующие оси координат). Углы, образованные главным вектором с соответствующей осью координат:

, , . (7)

Модуль главного момента относительно выбранного центра приведения O:

(8)

где , (9)

( , , — проекции главного момента относительно точки О на координатные оси).

Если заданы проекции сил на оси и координаты точек их приложения, то выражения (9) имеют вид

, , (10)

Углы, образованные главным моментом с соответствующими осями координат:

, , . (11)

Зависимость главного момента от выбора центра приведения

Главный момент относительно нового центра приведения равен сумме главного момента относительно старого центра приведения и векторного произведения радиуса-вектора, соединяющего эти центры, на главный вектор:

. (12)

где — главный момент относительно центра ; — главный момент относительно центра ; — радиус-вектор, соединяющий центры и ; — главный вектор.

Частные случаи приведения системы сил

В зависимости от модулей главного вектора и главного момента и их взаимного направления можно произвести дальнейшее упрощение системы сил.

1. Приведение к паре сил

, , .

Система сил приводится к одной паре сил, равной главному моменту и не зависящей от выбора центра приведения.

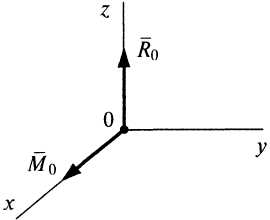
2. Приведение к равнодействующей

a) , , .

Система сил приводится к равнодействующей, равной главному вектору по модулю и направлению и проходящей через центр приведения.

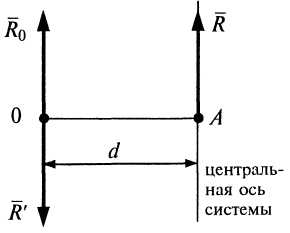
б) , , , т.е. .

Система сил приводится к равнодействующей, равной по модулю и направлению главному вектору и отстоящей от центра приведения на расстоянии . Линия действия равнодействующей называется центральной осью системы.

3. П

   Рисунок

   Рисунок 5

   риведение системы сил к динаме (динамическому винту)

, , .

Система сил приводится к динаме (динамическому винту). Динамой называют совокупность силы и пары сил, векторный момент которой направлен параллельно вектору силы. Линию действия динамы называют центральной винтовой осью (рис.).

Г

Рисунок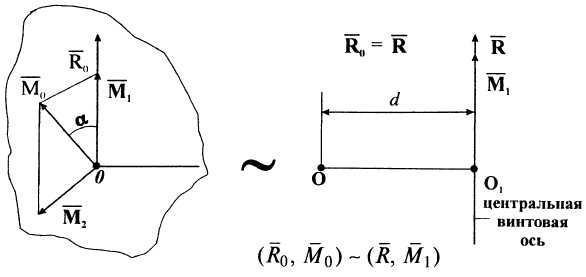

лавный момент раскладываем на направление главного вектора и перпендикулярно главному вектору: , , .

Так как (рис. а), то эта система сил приводится к равнодействующей, которая находится от точки приведения на расстоянии: . Пара сил с векторным моментом является свободным вектором и поэтому перенесем в точку , где приложена равнодействующая (рис. б). Получим в точке систему, эквивалентную исходной системе сил: , где — динама.

Теорема Вариньона о моменте равнодействующей

Момент равнодействующей системы сил относительно произвольной точки равен геометрической сумме моментов составляющих сил относительно этой точки:

(13)

Момент равнодействующей системы сил относительно любой оси равен алгебраической сумме моментов составляющих сил относительно этой оси:

(14)