
- •Раздел 2. Кинематика.
- •Тема 1. Введение в кинематику
- •Тема 2. Кинематика точки
- •Способы задания движения точки. Скорость и ускорение
- •Тема 3. Простейшие движения твердого тела. Поступательное движение твердого тела
- •Тема 4. Сложное движение точки
- •Тема 5. Плоское движение твердого тела.
- •Тема 6. Движение твердого тела вокруг неподвижной точки. (сферическое движение)
- •Тема 7. Движение свободного твердого тела.
- •Тема 8. Сложное движение твердого тела
- •1. Вращения имеют одинаковые направления
- •2. Вращения имеют противоположные направления с неравными угловыми скоростями
- •3. Пара вращений (вращения имеют противоположные направления с равными угловыми скоростями)
- •1. Скорость поступательного движения перпендикулярна оси относительного движения
- •2. Скорость поступательного переносного движения параллельна вектору угловой скорости относительного вращения
- •3. Скорость поступательного переносного движения направлена под углом к вектору угловой скорости относительно вращательного движения
Раздел 2. Кинематика.
Тема 1. Введение в кинематику
Кинематика — это раздел теоретической механики, в котором изучают механическое движение материальных тел без рассмотрения условий, вызывающих или изменяющих это движение.
Движение материальных тел происходит в пространстве и во времени. Пространство рассматривают как трехмерное евклидово, время в этом пространстве одинаково во всех его точках и не зависит от движения материальных тел.
Под механическим движением понимают изменение положения одного тела относительно другого.
Системой отсчета называют систему координат, связанную с одним из тел. Если тело движется, то система отсчета подвижна, если тело в покое, то система отсчета неподвижна.
Основные задачи кинематики
Установление закона движения тела по отношению к выбранной системе отсчета.
Определение по заданному закону движения тела кинематических характеристик этого движения (траектория, скорость, ускорение, угловые скорость и ускорение и т. д.)
Тема 2. Кинематика точки
Простейшим материальным телом, изучаемым в теоретической механике, является материальная точка. Материальной точкой считают твердое тело, размерами которого в данной задаче пренебрегают. Движение точки считают заданным, если известен способ, позволяющий установить ее положение относительно выбранной системы отсчета в любой момент времени.
Траекторией называют геометрическое место последовательных положений движущейся точки в выбранной системе отсчета. Движение точки называют криволинейным, если точка перемещается по кривой линии, и прямолинейным, если она перемещается по прямой линии. При этом вид траектории зависит от системы отсчета.
Существуют три способа задания движения точки: векторный, координатный, естественный.
Способы задания движения точки. Скорость и ускорение
Векторный способ задания движения заключается в задании положения точки радиусом-вектором, который является векторной функцией времени, относительно выбранной точки отсчета.
![]() .
(1)
.
(1)
Э та
функция должна быть однозначной и
непрерывной. Выражение
(1) называют законом
движения точки в векторной форме.
та
функция должна быть однозначной и
непрерывной. Выражение
(1) называют законом
движения точки в векторной форме.
Т
Рисунок 1![]() при изменении времени,
т. е. годограф
радиуса-вектора.
при изменении времени,
т. е. годограф
радиуса-вектора.
Годограф — это кривая, которую описывает конец радиуса-вектора при изменении его аргумента, когда начало вектора находится в одной и той же точке (рис. 1).
Скорость точки характеризует быстроту и направление движения точки и равна производной радиуса-вектора точки по времени:
![]() (2)
(2)
В механике производную по времени обозначают точкой над переменной.
Н аправление
вектора скорости можно
определить, используя понятие
производной вектора по скалярному
аргументу, которая всегда
направлена по касательной к годографу
этого вектора.
аправление
вектора скорости можно
определить, используя понятие
производной вектора по скалярному
аргументу, которая всегда
направлена по касательной к годографу
этого вектора.
Вектор скорости точки направлен по касательной к траектории точки в сторону ее движения (рис. 1).
У
Рисунок 2
![]() (3)
(3)
Вектор ускорения направлен по касательной к годографу вектора скорости (рис. 2).
Координатный способ задания движения заключается в задании координат точки в виде известных, непрерывных, дважды дифференцируемых функций времени.
Системы координат могут быть различными: декартовы, полярные, сферические, цилиндрические и т. д. В декартовой системе координат уравнениями движения точки будут
![]() ,
,
![]() ,
,
![]() (4)
(4)
Переход от векторного способа к координатному. Начало декартовой системы координат поместим в точке О, относительно которой задано движение точки М в векторной форме (рис. 3): .
Р азложим
радиус-вектор по
координатным осям, используя
единичные векторы
азложим
радиус-вектор по
координатным осям, используя
единичные векторы
![]() :
:
![]() (5)
(5)
Так как проекции радиуса-вектора
равны координатам точки, то
![]() ,
,
![]() ,
,
![]() .
.
С
Рисунок 3![]() .
(6)
.
(6)
Если использовать выражение (4), то можно записать
![]() .
(7)
.
(7)
Из выражения (7) следует, что если известно движение точки в координатной форме, то можно перейти к векторному способу задания движения.
Уравнения движения (4) являются
также уравнениями траектории точки в
параметрическом виде. Чтобы получить
уравнение траектории в координатной
форме, необходимо исключить время из
уравнений (4). Для этого выразим t
из уравнения
,
т.
е.
![]() ,
и
подставим его в остальные уравнения:
,
и
подставим его в остальные уравнения:
![]() ,
,
![]() (8)
(8)
Скорость точки в декартовых координатах:
![]() .
.
Отсюда
следует
![]() ,
,
![]() ,
,
![]() ,
(9)
,
(9)
где
![]() ,
,
![]() ,
,
![]() — проекции вектора скорости на
соответствующие оси координат;
— проекции вектора скорости на
соответствующие оси координат;
![]() (10)
(10)
Находим углы вектора скорости с осями координат:
![]() ,
,
![]() ,
,
![]() .
(11)
.
(11)
Ускорение точки в декартовых координатах:
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() (12)
(12)
(ax, ay, az — проекции вектора ускорения на соответствующие оси координат):
![]() .
(13)
.
(13)
Находим углы вектора ускорения с осями координат:
![]() ,
,
![]() ,
,
![]() .
(14)
.
(14)
Естественный способ задания движения считается известным, если заданы:
Т
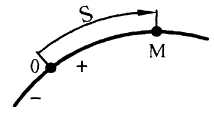 раектория
точки.
раектория
точки.Закон движения точки по траектории
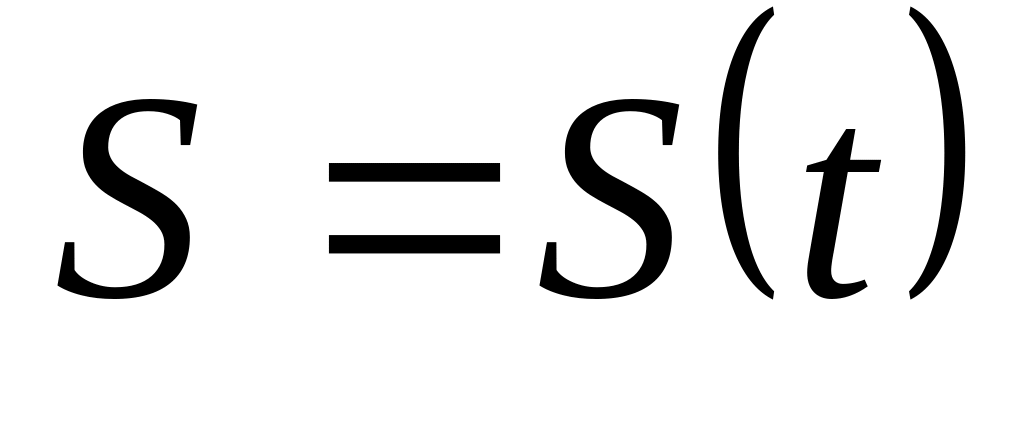 .
.Начало отсчета.
П
Рисунок 4
оложительное и отрицательное направления движения.
Закон движения также называют дуговой координатой, которую отсчитывают от начального положения (рис. 4). Дуговую координату не следует смешивать с длиной пути, пройденного точкой, так как за начало отсчета может быть выбрана любая точка или движение может быть колебательным.
П
Рисунок 5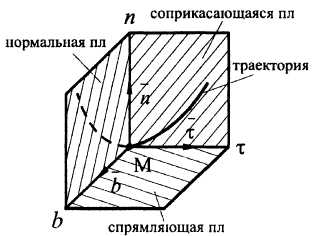
![]() — касательная,
— касательная,
![]() — нормаль,
— нормаль,
![]() — бинормаль (рис. 5);
— бинормаль (рис. 5);
— касательная является линией пересечения соприкасающейся и спрямляющей плоскостей.
— нормаль является линией пересечения соприкасающейся и нормальной плоскостей.
— бинормаль является линией пересечения нормальной и спрямляющей плоскостей.
При
движении точки по кривой естественные
оси перемещаются
вместе с точкой, образуя правую систему
координат,
,
являются
единичными векторами, направленными
по
трем взаимно перпендикулярным осям
![]() ,
,
![]() ,
,
![]() .
.
Скорость точки при естественном способе задания движения.
З а
время
а
время
![]() точка
М
по
траектории перешла в положение
точка
М
по
траектории перешла в положение
![]() (рис.
6). За это время дуговая координата
изменилась на
(рис.
6). За это время дуговая координата
изменилась на
![]() ,
а
радиус-вектор — на
,
а
радиус-вектор — на
![]() .
Используя определение скорости, запишем:
.
Используя определение скорости, запишем:
![]() .
.
Обозначим
![]() ,
,
![]() .
.
В
Рисунок 6![]() .
.
Скалярную величину
![]() ,
представляющую проекцию вектора скорости
на касательную, называют алгебраической
скоростью
точки.
Если
,
представляющую проекцию вектора скорости
на касательную, называют алгебраической
скоростью
точки.
Если
![]() ,
то вектор скорости направлен по
,
т.
е. в сторону возрастания значений S
(рис.
6), а если
,
то вектор скорости направлен по
,
т.
е. в сторону возрастания значений S
(рис.
6), а если
![]() ,
то вектор скорости
направлен в сторону убывающих значений
дуговой координаты. Тогда
,
то вектор скорости
направлен в сторону убывающих значений
дуговой координаты. Тогда
![]() (15)
(15)
Или
![]() (16)
(16)
Ускорение точки при естественном способе задания движения.
Для определения ускорения дифференцируем выражение (16) по времени:
![]() ,
(17)
,
(17)
где
![]() .
Тогда
формула (17) примет вид
.
Тогда
формула (17) примет вид
![]() ,
(18)
,
(18)
У
Рисунок 7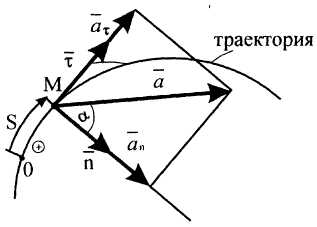
![]() направлена по касательной к траектории,
а другая
направлена по касательной к траектории,
а другая
![]() — по нормали к этой траектории в сторону
ее вогнутости. Эти составляющие называют
соответственно касательным и
нормальным ускорениями точки.
Они лежат в соприкасающейся плоскости.
Проекция ускорения точки на бинормаль
равна нулю, так как вектор ускорения
расположен в соприкасающейся плоскости:
— по нормали к этой траектории в сторону
ее вогнутости. Эти составляющие называют
соответственно касательным и
нормальным ускорениями точки.
Они лежат в соприкасающейся плоскости.
Проекция ускорения точки на бинормаль
равна нулю, так как вектор ускорения
расположен в соприкасающейся плоскости:
![]() (19)
(19)
Вектор касательного ускорения
![]() ,
(20)
,
(20)
модуль касательного ускорения
![]() .
(21)
.
(21)
Вектор нормального ускорения
![]() ,
(22)
,
(22)
модуль нормального ускорения
![]() .
(23)
.
(23)
Модуль ускорения равен:
![]() .
(24)
.
(24)
Угол отклонения вектора ускорения от нормали составит (рис. 7):
![]() .
(25)
.
(25)
Касательное ускорение характеризует изменение скорости по модулю, а нормальное — изменение скорости по направлению.
Касательное и нормальное ускорения точки можно определить при ее движении в плоскости через проекции скорости и ускорения в декартовых координатах, используя выражения (10), (21), (24):
![]() ,
,
![]() (26-27)
(26-27)
Классификация движения по ускорениям

 ,
,
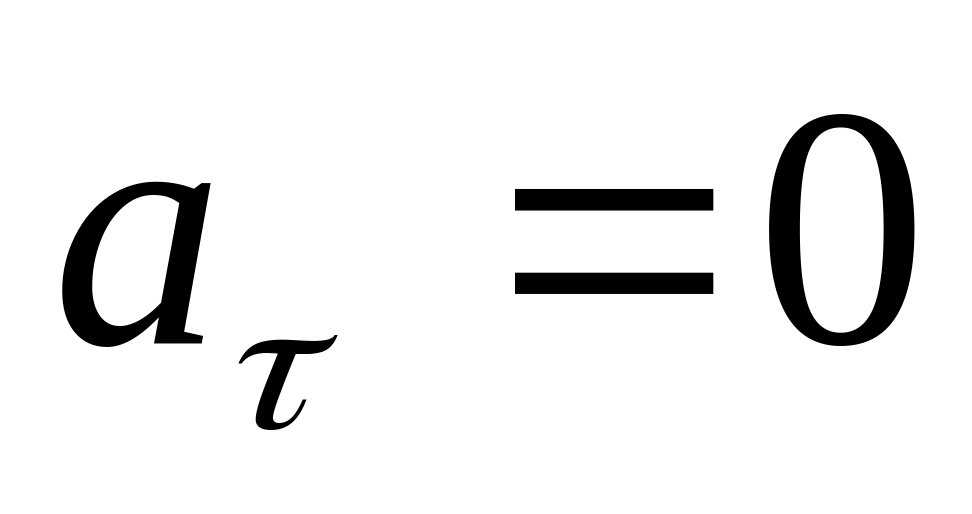 .
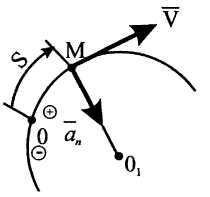
Движение прямолинейное и равномерное.
.
Движение прямолинейное и равномерное.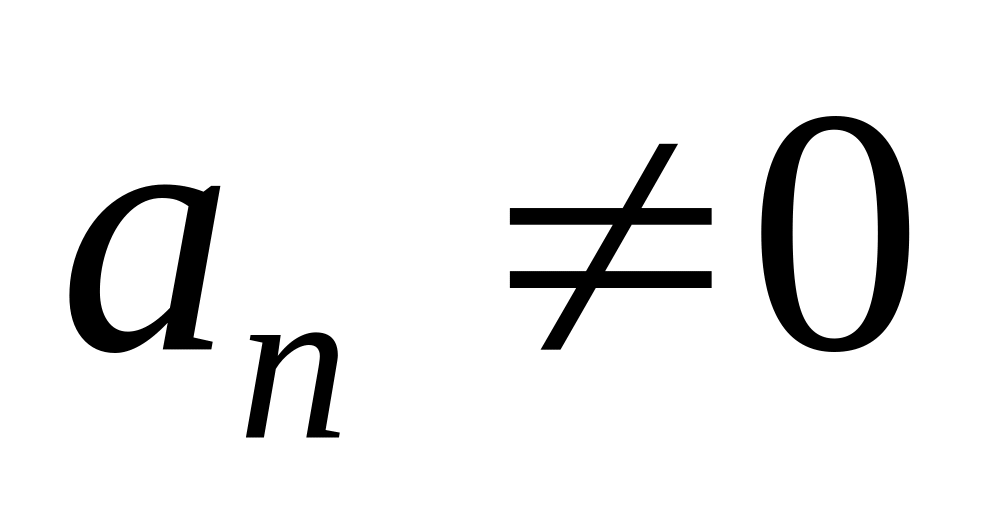 ,
,
 .
Движение
криволинейное и равномерное (рис.
8).
.
Движение
криволинейное и равномерное (рис.
8). ,
,
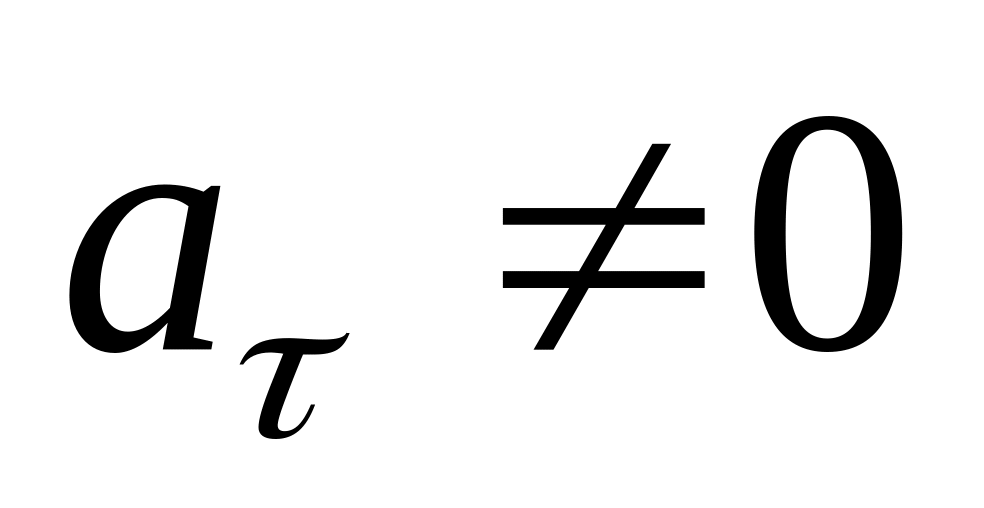 .
Движение прямолинейное
и неравномерное.
.
Движение прямолинейное
и неравномерное.П
Рисунок 8
рямолинейное, ускоренное (рис. 9)

Рисунок 9
Прямолинейное, замедленное (рис. 10)

Рисунок 10
 ,
,
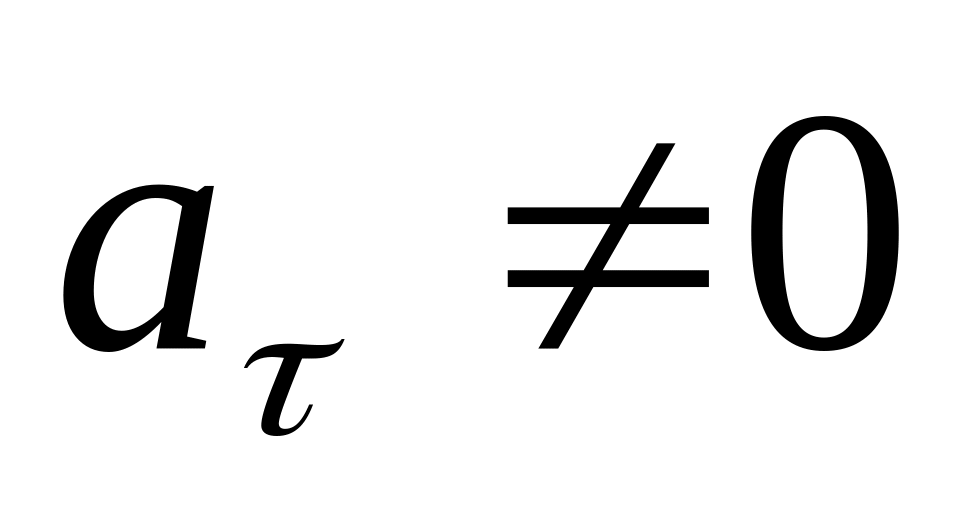 .
Движение криволинейное и неравномерное.
.
Движение криволинейное и неравномерное.Криволинейное, ускоренное (
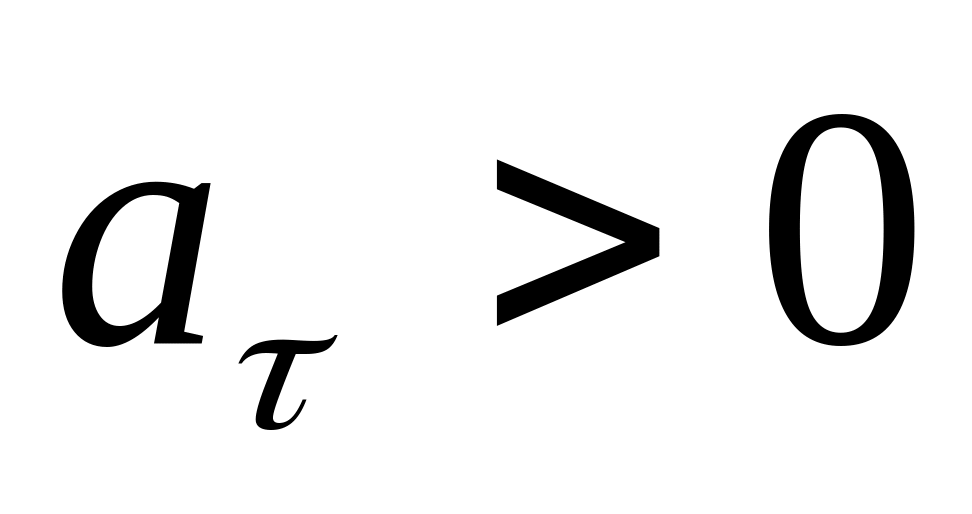 ,
,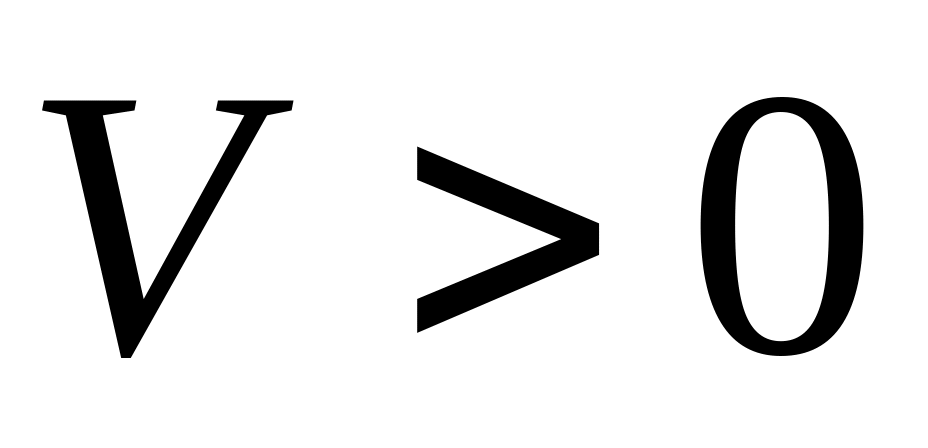 )(рис.
11)
)(рис.
11)
Криволинейное, замедленное (рис. 12, а, б)
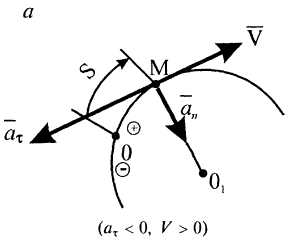
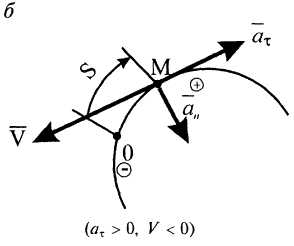
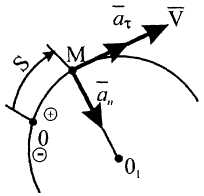
Рисунок 11
Рисунок 12
Уравнения движения точки
Уравнение
равномерного движения
по траектории любой формы,
![]()
![]() (28)
(28)
Уравнение
равнопеременного движения по траектории
любой
формы
![]()
![]() (29)
(29)
где
![]() —
начальное положение;
—
начальное положение;
![]() —
начальная скорость. Если
—
начальная скорость. Если
![]() ,
то движение равноускоренное. Если
,
то движение равноускоренное. Если
![]() ,
то движение равнозамедленное. Скорость
равнопеременного движения
,
то движение равнозамедленное. Скорость
равнопеременного движения
![]() (30)
(30)
Переход от координатного к естественному способу задания движения
Задано движение точки координатным способом: , , . Для перехода от координатного способа к естественному необходимо:
Установить траекторию, если возможно, т. е. получить уравнение траектории в явном виде:
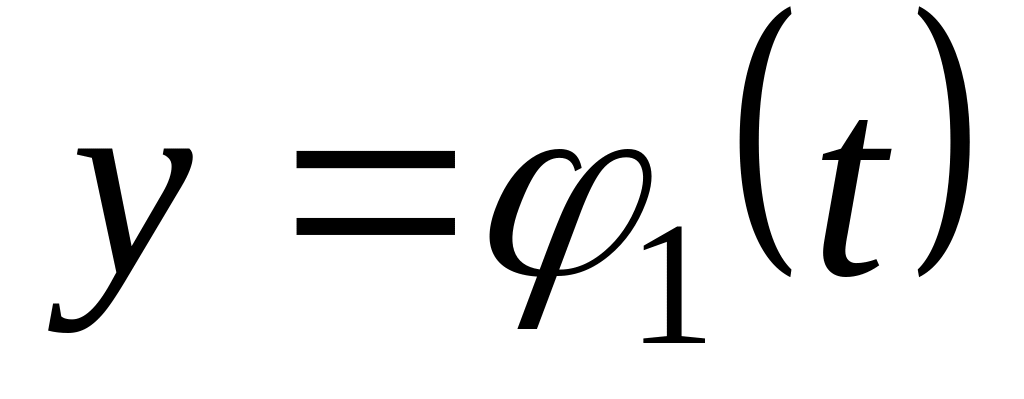 ,
,
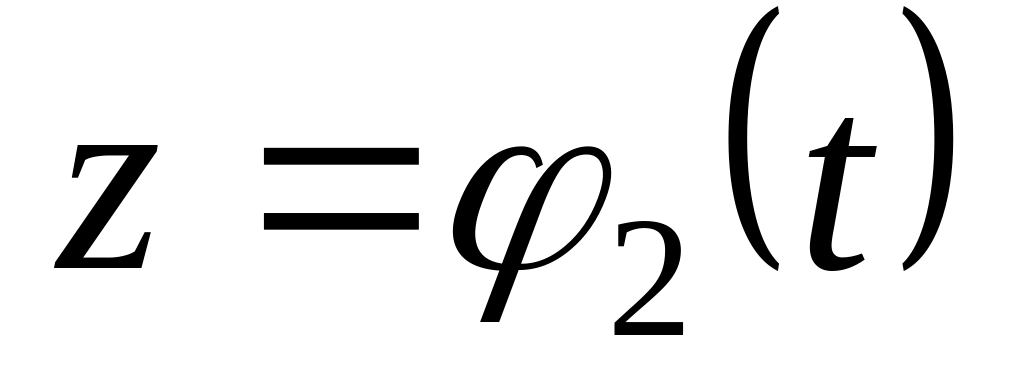 .
.Определить закон движения по этой траектории по формуле:
![]() .
.
Установить начало отсчета, подставив в уравнения движения начальное время. Если это время не задано, подставляют
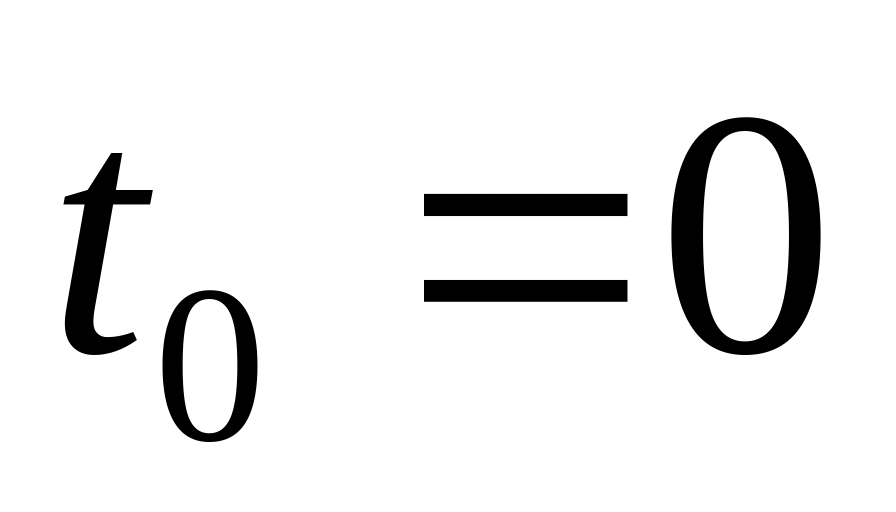 .
.Определить положительное направление движения, которое можно узнать или по вектору скорости, или, задавая значения времени в уравнения движения, чтобы получить новую точку на траектории.
