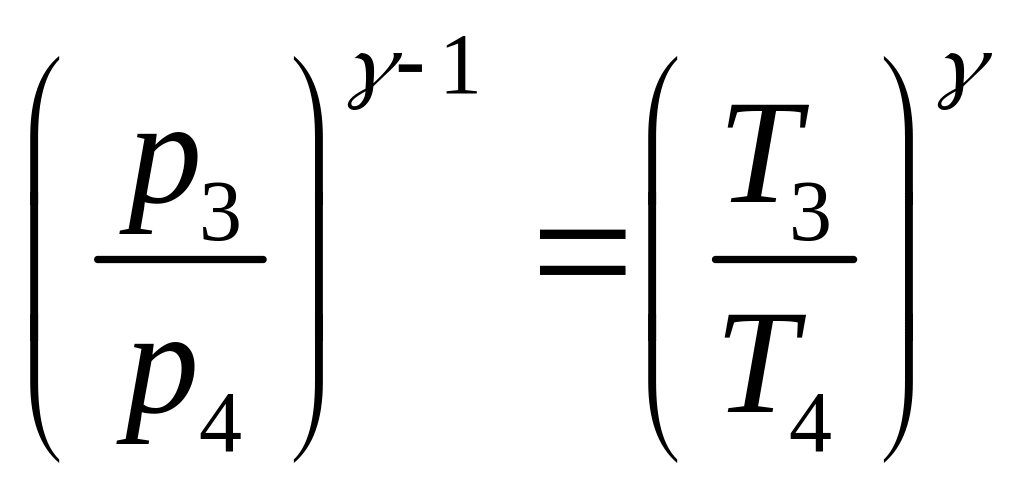Введение.Теплоемкость идеального газа.

Для характеристики макроскопических тепловых свойств систем пользуются особым параметром – теплоёмкостью системы.

Теплоёмкость C термодинамической системы численно равна количеству теплоты dQ, которое необходимо передать системе (или отвести от неё), чтобы изменить её температуру T на 1 К (или 1 °С); точнее – это отношение количества теплоты, поглощаемой телом при бесконечно малом изменении его температуры, к этому изменению:

,

(1)

где dQ – переданное системе количество теплоты, dT – бесконечно малое изменение температуры.

Удельной теплоёмкостью вещества c называется величина, равная количеству теплоты, которую необходимо сообщить единице массы вещества для увеличения ее температуры на 1 К:

,

(2)

где m – масса.

Для газов удобно пользоваться молярной теплоёмкостью C_m – количеством теплоты, необходимым для нагревания одного моля данного вещества на 1 К:

→ Cm = cμ,

(3)

где µ – молярная масса вещества;  – количество молей вещества; c – удельная теплоёмкость.

Молярная теплоёмкость в системе СИ измеряется в Дж·моль^–1·К^–1 (в дальнейшем молярную теплоемкость будем обозначать С).

Теплоёмкость газов зависит от строения молекулы данного газа – числа атомов в молекуле и их взаимного расположения, т. е. от количества степеней свободы данной молекулы. С другой стороны, теплоемкость зависит от типа термодинамического процесса.

Число степеней свободы i  в механике – это число независимых координат, определяющих положение механической системы в пространстве, причем таких, по которым элементы системы могут двигаться. Например, поршень в цилиндре может двигаться только по оси цилиндра, поэтому у него одна степень свободы. В соответствии с характером этого движения различают поступательные, вращательные и колебательные степени свободы.

При определении числа степеней свободы для молекулы ее можно рассматривать как систему материальных точек – атомов.

Для одноатомной молекулы i = 3 (три поступательные степени свободы, соответствующие перемещениям вдоль осей X, Y и Z).

Для двухатомной молекулы (например, N₂ или H₂) с жёсткой внутренней связью между атомами, т. е. при неизменном расстоянии между атомами вдоль оси Y, i = 5 (три поступательные степени свободы её центра инерции и две вращательные, соответствующие вращениям вокруг осей X и Z). Вращение вокруг оси Y для такой модели молекулы не приводит ни к каким изменениям.

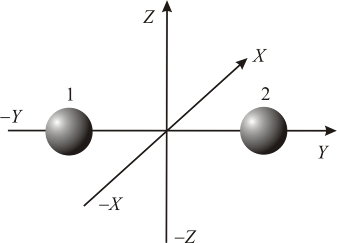
Рис. 1. Модель молекулы двухатомного газа

Для трёхатомной молекулы с жёсткими связями i = 6 (три поступательных и три вращательных степени свободы).

В классической статистической физике показано (закон равнораспределения энергии по степеням свободы), что на каждую степень свободы приходится в среднем энергия (где k – постоянная Больцмана; T – абсолютная температура).

Для молекул с упругой связью между атомами необходимо учесть колебательные степени свободы. Так как колебательное движение характеризуется наличием и потенциальной, и кинетической энергий, средние значения которых равны, то на каждую колебательную степень свободы в среднем приходится энергия в 2 раза больше. Однако при обычных (комнатных) температурах колебательные степени свободы не вносят вклад в теплоёмкость многоатомного газа, они выключены («заморожены»), так как могут возбуждаться лишь при достаточно высоких температурах.

.

(4)

Таким образом, средняя энергия E молекулы равна:

,

(5)

где i – сумма возможных степеней свободы молекулы; k – постоянная Больцмана; T – температура.

В соответствии с первым началом термодинамики количество теплоты dQ, подводимое к газу, может расходоваться на увеличение внутренней энергии газа dU и на совершение термодинамической работы dA при расширении газа:

.

(6)

Увеличение внутренней энергии идеального газа в случае изменения его температуры на dT рассчитывается по формуле:

.

(7)

где R – универсальная газовая постоянная (R ≈ 8,31 10³ Дж·кмоль^–1·К^–1).

При расширении газа система выполняет работу dA:

dA = pdV.

(8)

Величина теплоёмкости существенно зависит от того, при каких условиях нагревался газ.

1. Изохорический процесс, протекающий при постоянном объёме системы, V = const. В этом случае работа по расширению газа отсутствует (ΔV =0, поэтому A = pΔV = 0) и dQ = dU, следовательно, молярная теплоёмкость газа при постоянном объёме C_V:

(9)

2. Изобарический процесс, протекающий при постоянном давлении системы, p = const. В этом случае работа не равна нулю.

Тогда .

(10)

где C_p – молярная теплоёмкость газа при постоянном давлении.

Итак, при нагревании при постоянном давлении часть теплоты идёт на производство работы расширения тела, а часть – на увеличение его внутренней энергии, тогда как при нагревании при постоянном объёме вся теплота расходуется на увеличение внутренней энергии, и C_p всегда больше, чем C_V.

Используя уравнение состояния идеального газа (уравнение Менделеева–Клапейрона):

,

(11)

можно показать, что для одного моля газа:

.

(12)

Поэтому уравнение (10) можно переписать в виде формулы Мáйера:

,

(13)

Тогда, разделив C_p на C_V, получим:

.

(14)

Величина γ имеет самостоятельный смысл в термодинамике, она входит в уравнение описывающие адиабатический процесс - уравнение Пуассóна, называется показателем адиабаты или коэффициентом Пуассóна.

Адиабатический процесс - это процесс, протекающий без теплообмена системы с окружающей средой, dQ = 0. На практике адиабатическими процессами являются те процессы, которые протекают очень быстро, и теплообмен с окружающей средой не успевает произойти, или же процессы, протекающие в системах, находящихся в термостате (например в термосе). Уравнение адиабаты:

(15)

Это - уравнение Пуассона. С учетом уравнения Клапейрона - Менделеева уравнение можно переписать, используя другие параметры состояния идеального газа (всюду ν =const):

	(16)
	(17)

как видно из (14), γ для любого идеального газа зависит только от числа степеней свободы его молекул.

Табл. 1. Число степеней свободы для некоторых молекул

Молекула	Связь между атомами	Число степеней свободы			i	Cp/CV
		Пост.	Вр.	Кол.
Одноатомная	-	3	0	0	3	1,67
Двухатомная	Жёсткая	3	2	0	5	1,40
	Упругая	3	2	1	6	1,291
Трёхатомная	Жёсткая	3	3	0	6	1,33

Впервые измерение отношения теплоёмкостей для газов было осуществлено французскими химиками Н. Клемáном и Ш. Дезóрмом в 1819 г, метод основывается на изучении параметров некоторой массы газа, переходящей из одного состояния в другое двумя последовательными процессами – адиабатическим и изохорическим.

Лабораторная работа 9

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЁМКОСТЕЙ ГАЗОВ МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ (МЕТОДОМ КЛЕМАНА И ДЕЗОРМА)

Цели и задачи работы

1. Изучение термодинамических процессов в воздухе.

2. Определение показателя адиабаты γ для воздуха адиабатическим методом Клемана и Дезорма.

Ф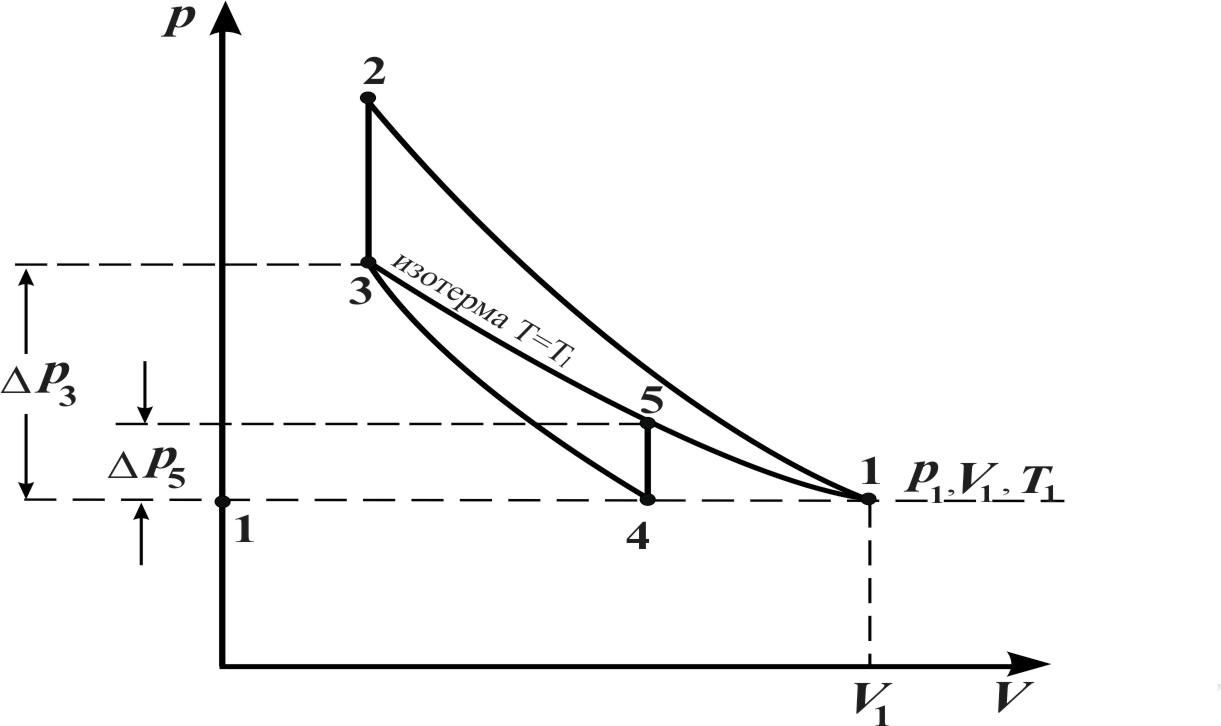 изическое обоснование эксперимента

Рис. 9.1. pV-диаграмма процессов в газе: 3-4 – адиабатический процесс; 2-3 и 4-5 – изохорические процессы

Выделим мысленно в сосуде некоторую порцию газа (ν молей)_, и в дальнейшем будем рассматривать изменения происходящие только с этой порцией.

Исходное состояние 1 характеризуется параметрами p₁, V₁ и T₁, где p₁ - атмосферное давление, T₁ – комнатная температура.

Накачаем в сосуд воздух (процесс 1-2). При этом газ в сосуде сожмётся и нагреется (состояние 2).

После отключения сосуда от насоса (перекрывания крана) газ будет остывать до комнатной температуры при постоянном объеме (изохорический процесс 2-3). Соответственно примет объем V₃ (V₃= V₂)_, и температуру Т₃ (Т₃ =Т₁). в состоянии 3 давление p₃ установится больше атмосферного на Δp₃. Последняя величина определяется по разности уровней подкрашенной жидкости h₁ в коленах манометра М.

Если теперь на короткое время соединить баллон с атмосферой, то произойдёт быстрое, а, следовательно, адиабатическое расширение воздуха (процесс 3-4). При этом давление понизится до атмосферного p₄ = p₁. Рассматриваемая масса воздуха, займет объём V₄. При этом температура воздуха понизится до Т₄ < T₁.

Поскольку процесс 3-4 – адиабатический, к нему можно применить уравнение Пуассона:

	(9.1)
Или в соответствии с формулой 17 .	(9.2)
Это уравнение можно переписать в виде:
Учитывая, что p4 = p1, p3= p1+ Δp3, а Т3 =Т1 получаем: .	(9.3)

После адиабатического расширения воздух в баллоне будет нагреваться (процесс 4-5) до температуры окружающей среды Т₅ = Т₁ при постоянном объёме V₅ = V₄. При этом давление в баллоне поднимется до (p₅ = p₁ + Δp₅). Изменение давления Δp₅ можно определить по разности уровней подкрашенной жидкости h₂ в коленах манометра М. Поскольку процесс 4-5 – изохорический, к нему можно применить закон Шарля:

.

(9.4)

Сопоставив уравнения 9.3 и 9.4, получим:

.

(9.5)

Прологарифмируем:

.

(9.6)

Поскольку избыточные давления Δp₃ и Δp₅ малы по сравнению с атмосферным давлением p₁ и, учитывая, что для натуральных логарифмов ln(1 + x) ≈ x при x << 1, будем иметь:

,

(9.7)

откуда

.

(9.8)