Свойства преобразования Фурье
Рассмотрим основные свойства преобразования Фурье.
Линейность.
Рассмотрим функции
и
,
имеющие спектры
и
:
(12)
Тогда спектр их линейной комбинации будет:
(13)
Задержка во времени. Считаем, что известен спектр сигнала
(14)
Рассчитаем спектр
сигнала, сдвинутого во времени:
.
Обозначим аргумент функции новой
переменной
,
тогда
и
(15)
Получили, что
задержка сигнала на время
приводит к умножению спектра на
.
Изменение
масштаба. Считаем,
что известен спектр
сигнала
,
как через
выражается спектр сигнала
.
Вводим новую переменную
,
делаем замену переменной интегрирования
.
(16)
Умножение на
.
Как и в предыдущем случае, считаем, что
известен спектр
сигнала
.
Найдем спектр этого сигнала, умноженного
на
.
(17)
Таким образом,
умножение сигнала на
приводит к смещению спектра на
.
Спектр производной. В данном случае ключевым моментом является абсолютная интегрируемость функции. Из того, что интеграл от модуля функции должен быть ограничен, следует, что на бесконечности функция должна стремиться к нулю. Интеграл от производной функции берётся по частям, получившиеся внеинтегральные слагаемые равны нулю, так как на бесконечности функция стремится к нулю.
(18)
Спектр интеграла.
Найдем спектр сигнала
.
Причём будем считать, что
,
то есть у сигнала отсутствует постоянная
составляющая. Это требование необходимо,
чтобы внеинтегральные слагаемые были
равны нулю, когда интеграл берётся по
частям.
(19)
Теорема о свёртке.
Известно, что
и
спектры функций
и
соответственно. Требуется выразить
спектр свертки
через
и
.
Для этого в интеграле Фурье от свёртки
у одной из функций выполним замену
переменой
,
тогда в показателе экспоненты можно
сделать замену
.
В результате такой замены двукратный
интеграл будет равен произведению двух
интегралов Фурье.
(20)
Преобразование Фурье свёртки двух сигналов даёт произведение спектров этих сигналов.
Произведение
сигналов.
Известно, что
и
– спектры функций
и
соответственно. Требуется выразить
спектр произведения
через спектры
и
.
Подставим в интеграл Фурье вместо одного
из сигналов, например
,
его выражение через обратное преобразование
Фурье, а потом поменяем порядок
интегрирования.
(21)
Спектр произведения сигналов есть свёртка спектров этих сигналов.
Спектр дискретного сигнала
Особое внимание
стоит уделить дискретным сигналам, так
как именно такие сигналы используются
в цифровой обработке. Дискретный сигнал
в отличие от непрерывного является
последовательностью чисел, соответствующих
значениям непрерывного сигнала в
определённые моменты времени. Условно
дискретный сигнал можно рассматривать
как непрерывный сигнал, который в
определённые моменты времени принимает
какие-то значения, а в остальное время
равен нулю. Таким образом, например,
дискретный
сигнал может быть задан как произведение
непрерывного сигнала
на последовательность периодически
повторяющихся прямоугольных импульсов
– тактирующих импульсов (рис.1).
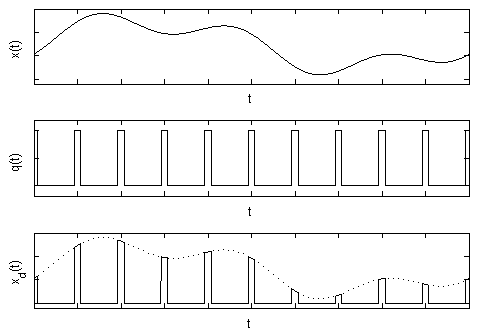
Рис. 1. Дискретизация сигнала.
(22)
Прямоугольные
импульсы имеют длительность
,
период повторения
:
(23)
Амплитуда импульса выбрана таким образом, чтобы интеграл импульса по периоду равнялся . При этом тактирующие импульсы безразмерны. Разложим последовательность таких импульсов в тригонометрический ряд:
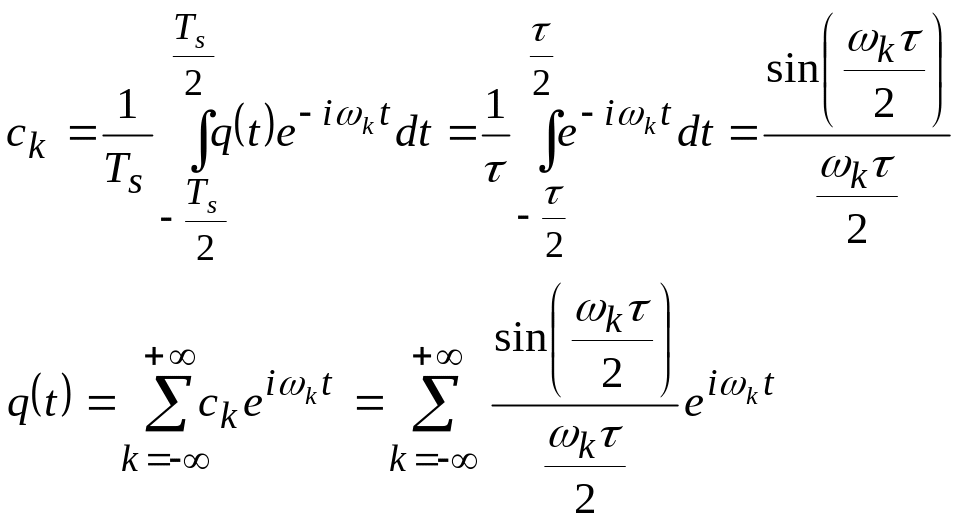(24)
Чтобы получить
мгновенные отсчёты сигнала
,
надо устремить к нулю длительность
импульсов к нулю:
.
Такой тактирующий сигнал назовём
идеальным. При этом коэффициенты
разложения
в ряд Фурье все будут равны 1.
(25)
Точно такой же вид имеет разложение в ряд Фурье функции:
(26)
Коэффициенты
разложения в тригонометрический ряд
тактирующего сигнала
:
(27)
Тогда дискретный сигнал будет иметь вид:
(28)
При вычислении преобразования Фурье дискретного сигнала меняем местами операцию суммировании и интегрирования, а потом используем свойство δ-функции:
(29)
Спектр дискретного
сигнала является периодической функцией.
Рассмотрим экспоненту в отельном
слагаемом
как функцию частоты. Её период повторения
равен
.
Самый большой период повторения у
слагаемых с номерами
,
и это, соответственно, будет периодом
повторения всего спектра. То есть
спектр дискретного сигнала имеет период
повторения, равный частоте квантования
.
Получим ещё одно
представление
.
В силу того, что
является произведением функций
и
,
спектр дискретного сигнала
вычисляется как свёртка спектров
непрерывного сигнала
и спектра тактирующего сигнала
.
(30)
Вычислим
,
используя (25). Так как
периодическая функция, её спектр
дискретный.
(31)
Таким образом, свёртка (30)
(32)
Из выражения (32)
следует, что спектр дискретного сигнала
представляет собой периодически
повторяющуюся функцию
.
Сам факт того, что в результате дискретизации в спектре сигнала происходят качественные изменения, говорит о том, что исходный сигнал может быть искажён, так как он полностью определяется своим спектром. Однако с другой стороны периодическое повторение одного и того же спектра само по себе не вносит ничего нового в спектр, поэтому при определённых условиях, зная значения сигнала в отдельные моменты времени, можно найти какое значение этот сигнал принимал в любой другой момент времени, то есть получить исходный непрерывный сигнал. В этом состоит смысл теоремы Котельникова, которая накладывает условие на выбор частоты квантования в соответствии с максимальной частотой в спектре сигнала.
Теорема
Котельникова:
чтобы непрерывный сигнал можно было
восстановить по его дискретным
отсчётам, необходимо, чтобы частота
квантования была выбрана больше
удвоенной максимальной частоты в
спектре сигнала
|
Если это условие нарушено, то после оцифровки сигнала произойдёт наложение периодически повторяющегося спектра (рис. 2). Получившийся в результате наложения спектр будет соответствовать другому сигналу.
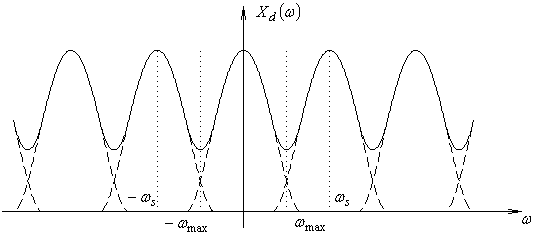
Рис. 2. Перекрывание спектров.