- •30 Кафедра математического анализа
- •Глава 2. Кратные интегралы
- •§1. Двойной интеграл. Свойства и методы вычисления
- •§2. Замена переменных в двойном интеграле
- •§3. Применения двойного интеграла
- •§4 Тройной интеграл. Свойства, вычисление, применение
- •Вычисление тройного интеграла
- •Задания для самостоятельного решения:
§4 Тройной интеграл. Свойства, вычисление, применение
Определение тройного интеграла
Тройной
интеграл является аналогом двойного
интеграла и вводится для функции трех
переменных. Пусть в пространственной
области
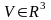 определена и непрерывна функция трех
переменных
определена и непрерывна функция трех
переменных
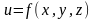 .
Разобьем область
на
.
Разобьем область
на
 произвольных областей
произвольных областей
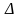 v1,
v2,…,
vn
с объемами
v1,
v2,…,
vn
с объемами
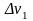 ,
,
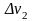 ,…,
,…,
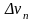 затем
выберем в каждой области
vi
произвольную точку
затем
выберем в каждой области
vi
произвольную точку
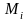 и построим интегральную сумму вида
и построим интегральную сумму вида
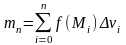 .
.
Если
интегральная сумма
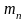 имеет предел при стремлении к нулю
наибольшего из диаметров областей
имеет предел при стремлении к нулю
наибольшего из диаметров областей
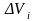 ,
то этот предел называется тройным
интегралом
и обозначается символом
,
то этот предел называется тройным
интегралом
и обозначается символом
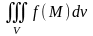 и
и
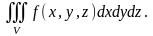
Тройной интеграл обладает свойствами, аналогичными свойствам двойного интеграла (линейность, аддитивность, оценка интеграла, свойство среднего).
Вычисление тройного интеграла
Пусть
функция трех переменных
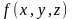 определена и непрерывна в пространственной
области
,
которая ограничена сверху поверхностью
определена и непрерывна в пространственной
области
,
которая ограничена сверху поверхностью
 ,
а снизу - поверхностью
,
а снизу - поверхностью
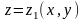 ,
где функции
,
где функции
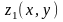 и
и
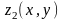 определены и непрерывны в области
определены и непрерывны в области
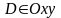 (рис.
19). Тогда вычисление тройного интеграла
сводится к последовательному (справа
налево) вычислению определенного
интеграла по переменной
(рис.
19). Тогда вычисление тройного интеграла
сводится к последовательному (справа
налево) вычислению определенного
интеграла по переменной
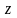 (переменные
и
считаются при этом константами) и
двойного интеграла от того, что получится,
по области
.
(переменные
и
считаются при этом константами) и
двойного интеграла от того, что получится,
по области
.

В
частности, если область
представляет собой прямоугольный
параллелепипед, определяемый неравенствами
 ,
,
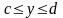 ,
,
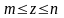 ,
то тройной интеграл сводится к трем
определенным интегралам:
,
то тройной интеграл сводится к трем
определенным интегралам:
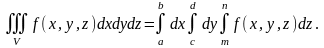
Естественно, можно выбирать другой порядок интегрирования.
Рис. 19. |
Рис. 20. |
Замена переменных в тройном интеграле
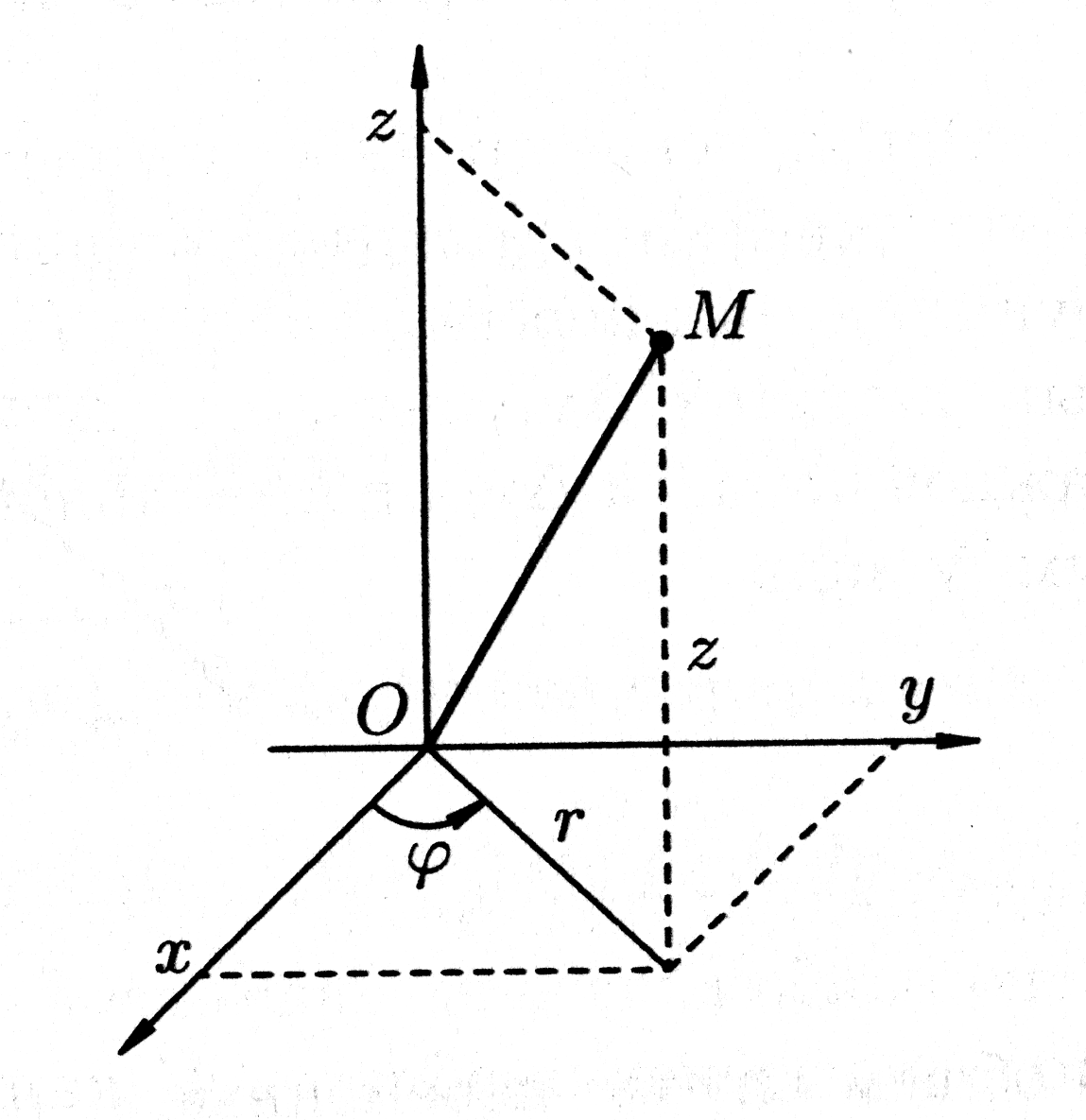
Цилиндрические координаты
Цилиндрические
координаты
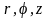 (рис.
20) представляют собой обобщение полярных
координат на плоскости и связаны с
прямоугольными координатами
(рис.
20) представляют собой обобщение полярных
координат на плоскости и связаны с
прямоугольными координатами
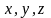 формулами
формулами
,
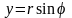 ,
,
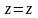 .
.
Переход к тройному интегралу в цилиндрических координатах осуществляется по формуле
 .
.
В частности, если
положить в этом равенстве
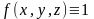 ,
то получим формулу для объема тела в
цилиндрических координатах:
,
то получим формулу для объема тела в
цилиндрических координатах:
 .
.
Сферические координаты
Сферические
координаты
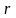 ,
,
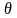 ,
связаны с прямоугольными координатами
при помощи формул (рис. 21)
,
связаны с прямоугольными координатами
при помощи формул (рис. 21)
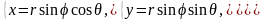
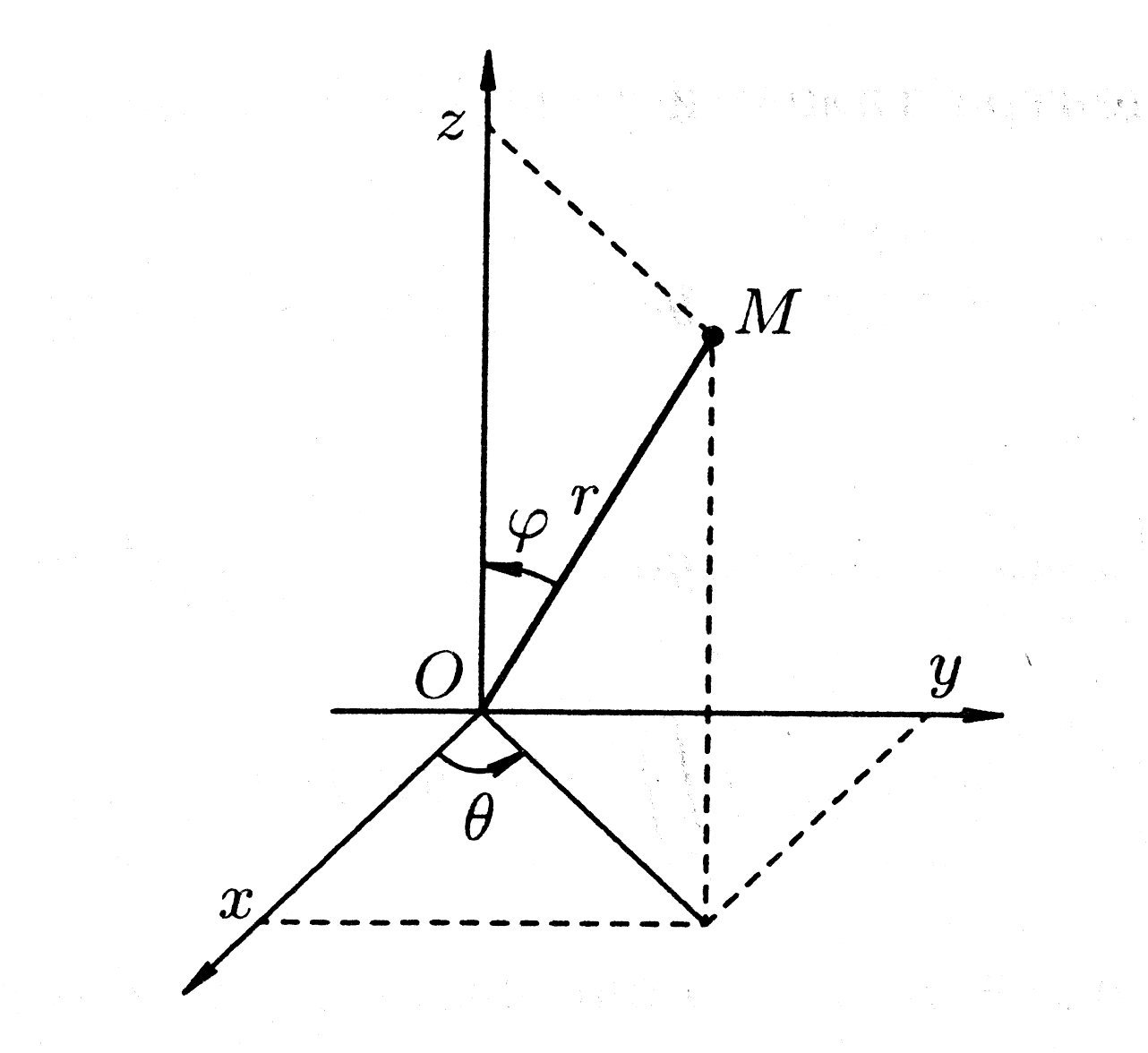
Рис. 21.
В
общем случае переменные
,
,
изменяются в пределах
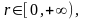
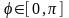 ,
,
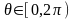 .
Формула перехода к сферическим координатам
имеет вид
.
Формула перехода к сферическим координатам
имеет вид
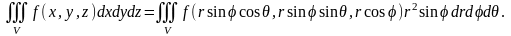
Положив , получим формулу для объема тела в сферических координатах:
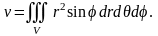
Приложения тройного интеграла
1. Объем тела находится по формуле:
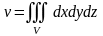 .
.
2.
Масса
тела
с данной плотностью
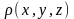 ,
где функция
непрерывна, вычисляется по формуле
,
где функция
непрерывна, вычисляется по формуле
 .
.
3.
Статические моменты
 ,
,
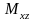 ,
,
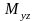 тела
относительно координатных плоскостей
,
тела
относительно координатных плоскостей
,
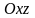 ,
соответственно равны
,
соответственно равны
 ,
,
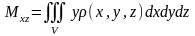 ,
,
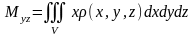 ,
,
где
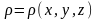 - плотность тела
.
- плотность тела
.
4. Координаты центра тяжести тела с массой определяются по формулам
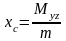 ,
,
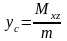 ,
,
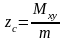 ,
,
или, более подробно:
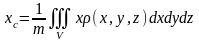 ,
,
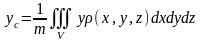 ,
,
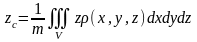 .
.
В
частности, если
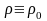 (тело однородно), эти формулы упрощаются:
(тело однородно), эти формулы упрощаются:
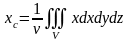 ,
,
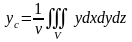 ,
,
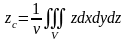 ,
,
где - объем тела .
5. Моменты инерции тела с плотностью относительно координатных плоскостей вычисляются по формулам
 ,
,
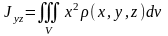 ,
,
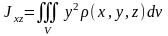 .
.
Моменты
инерции
,
и
 тела
относительно координатных осей
,
и
соответственно находятся по формулам
тела
относительно координатных осей
,
и
соответственно находятся по формулам
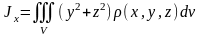 ,
,
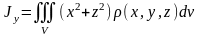 ,
,
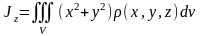 .
.
Пример 1. Вычислить тройной интеграл
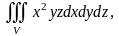
где
- область, ограниченная плоскостями
,
,
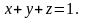
Область
(рис. 22) устроена просто, поэтому данный
тройной интеграл можно вычислить,
используя произвольный порядок
интегрирования. Обычно проектируют
область
на плоскость
,
принимая полученную проекцию в качестве
области
(на рис.
- треугольник
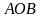 ).
Прямая, параллельная оси
,
пересекает границу
в двух точках. Аппликата первой точки
равна нулю (точка входа лежит на плоскости
,
т. е.
),
аппликата второй точки равна
).
Прямая, параллельная оси
,
пересекает границу
в двух точках. Аппликата первой точки
равна нулю (точка входа лежит на плоскости
,
т. е.
),
аппликата второй точки равна
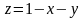 (поскольку точка выхода из области
лежит на плоскости
).
Таким образом,
(поскольку точка выхода из области
лежит на плоскости
).
Таким образом,
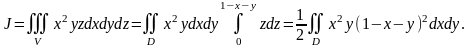
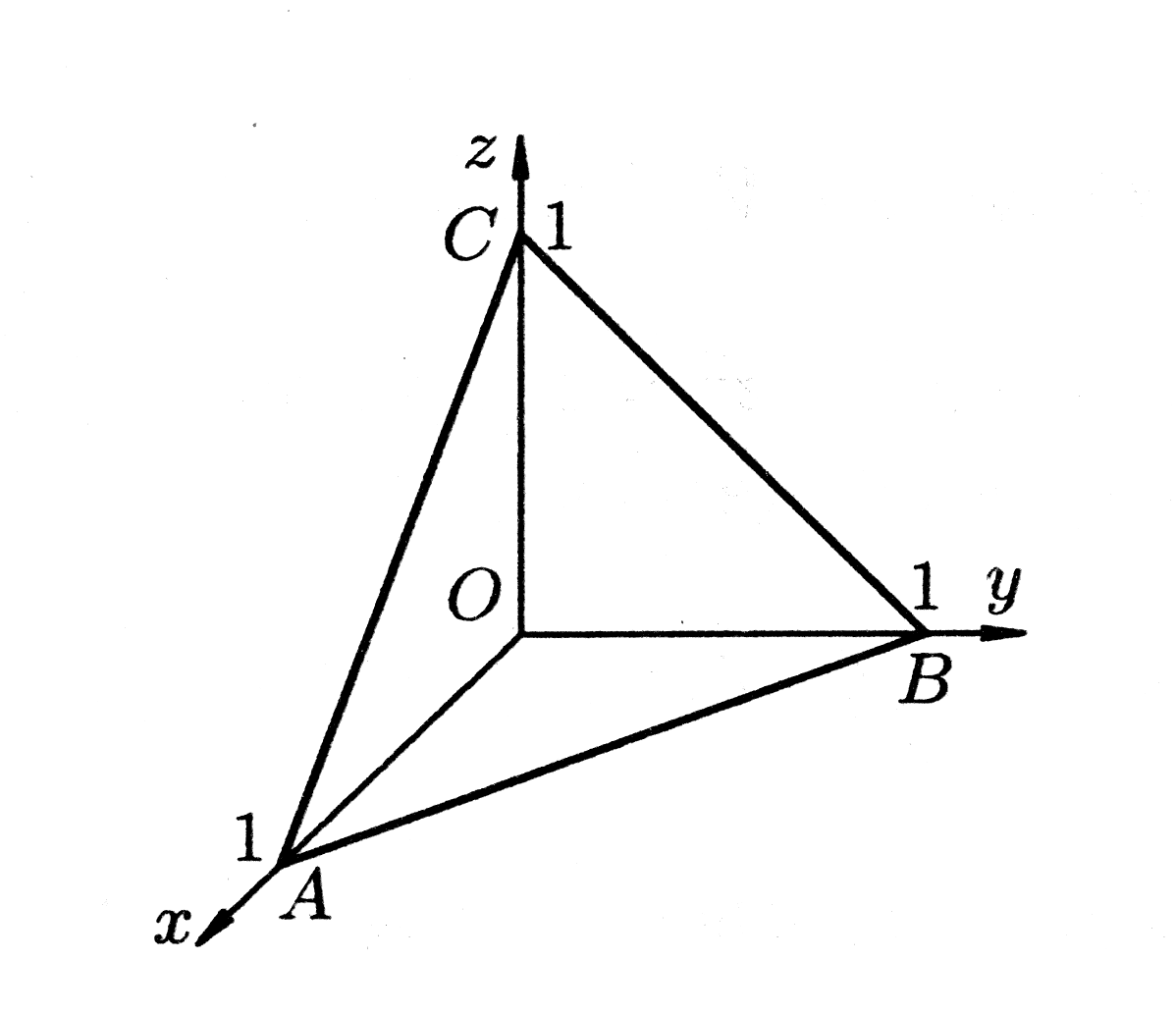
Рис. 22.
Двойной интеграл приводим к повторному.
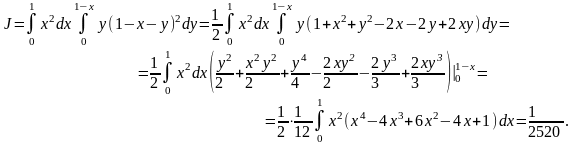
Пример 2. Вычислить тройной интеграл
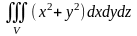 ,
,
если
ограничена плоскостью
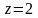 и параболоидом
и параболоидом
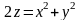 .
.
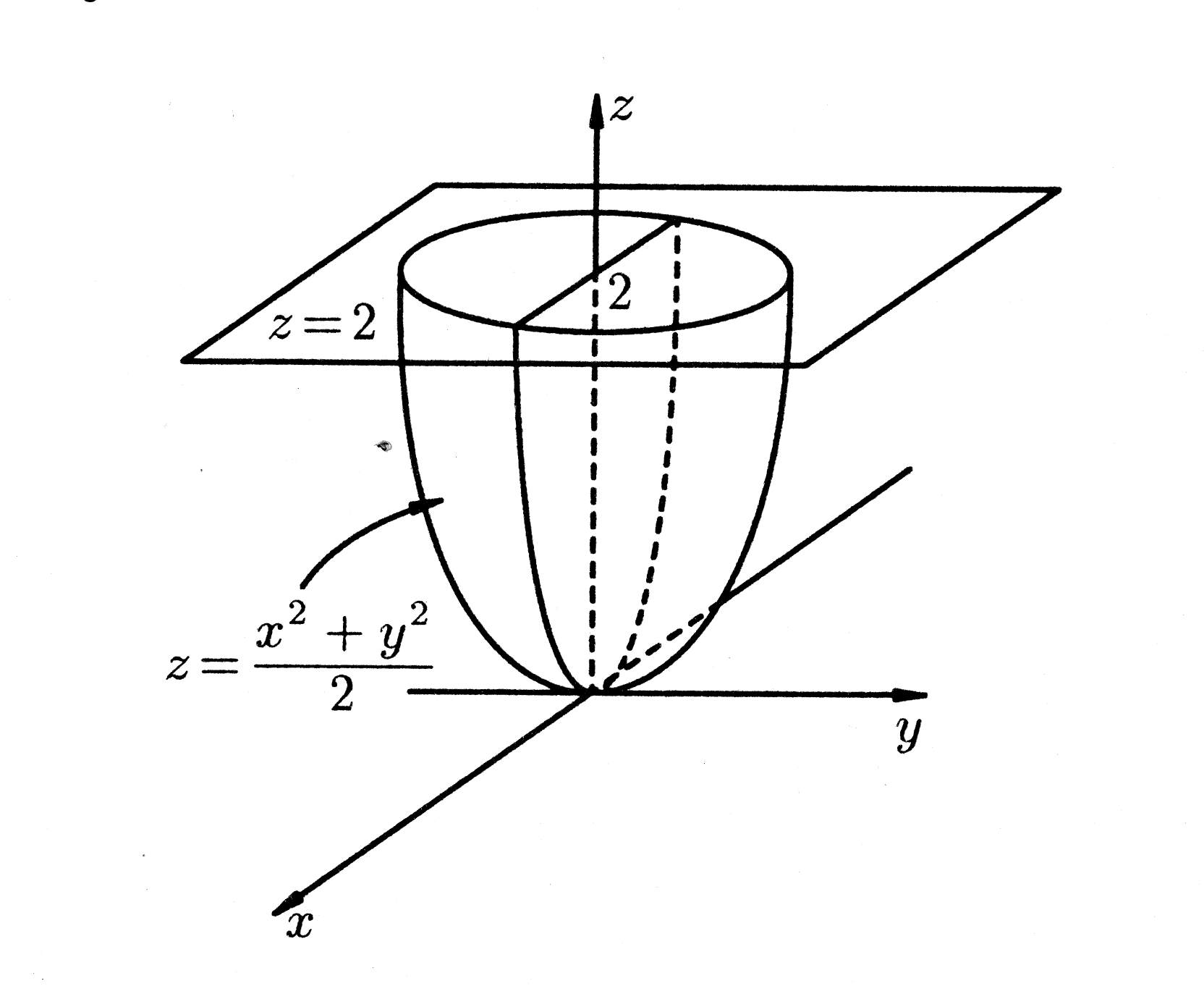
Рис. 23.
Область
ограничена сверху плоскостью
,
а снизу параболоидом
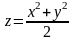 (рис. 23). Переходим к цилиндрическим
координатам
,
,
.
При этом подынтегральная функция
преобразуется к виду
(рис. 23). Переходим к цилиндрическим
координатам
,
,
.
При этом подынтегральная функция
преобразуется к виду
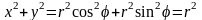 .
Таким образом,
.
Таким образом,
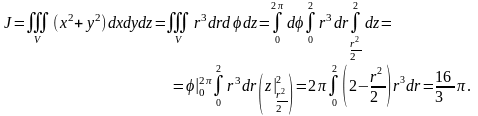
Пример 3. Вычислить повторный интеграл
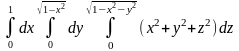 .
.
Преобразуем повторный интеграл в тройной
 ,
,
для
этого, исследуем пределы интегрирования
в повторном интеграле и восстанавливаем
область интегрирования
.
Она ограничена снизу плоскостью
,
т. е. плоскостью
,
а сверху – поверхностью
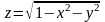 ,
т. е. верхней частью сферы
,
т. е. верхней частью сферы
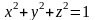 .
Область
лежит в плоскости
и ограничена снизу прямой
(осью
)
и сверху линией
.
Область
лежит в плоскости
и ограничена снизу прямой
(осью
)
и сверху линией
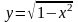 ,
т. е. верхней полуокружностью
,
т. е. верхней полуокружностью
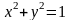 .
Наконец, проекция
на ось
- это отрезок
.
Наконец, проекция
на ось
- это отрезок
 .
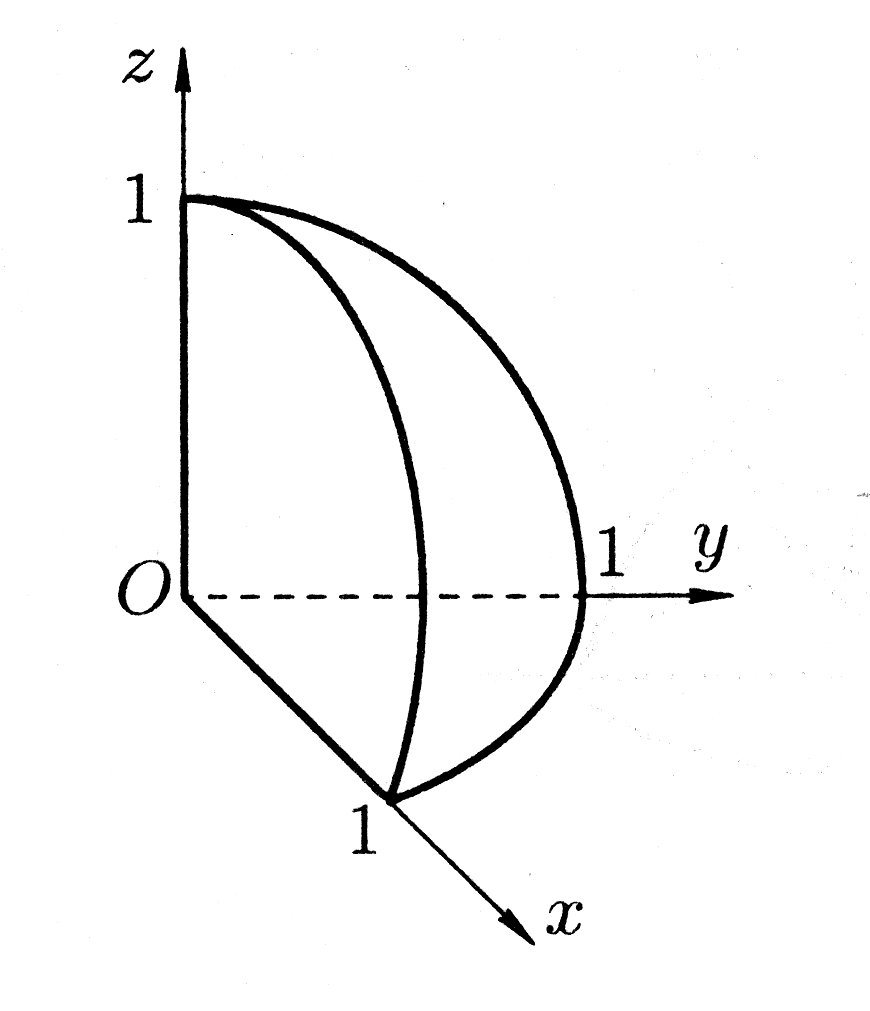
По названным поверхностям построим
чертеж области
(рис.24), а по соответствующим линиям –
область
.
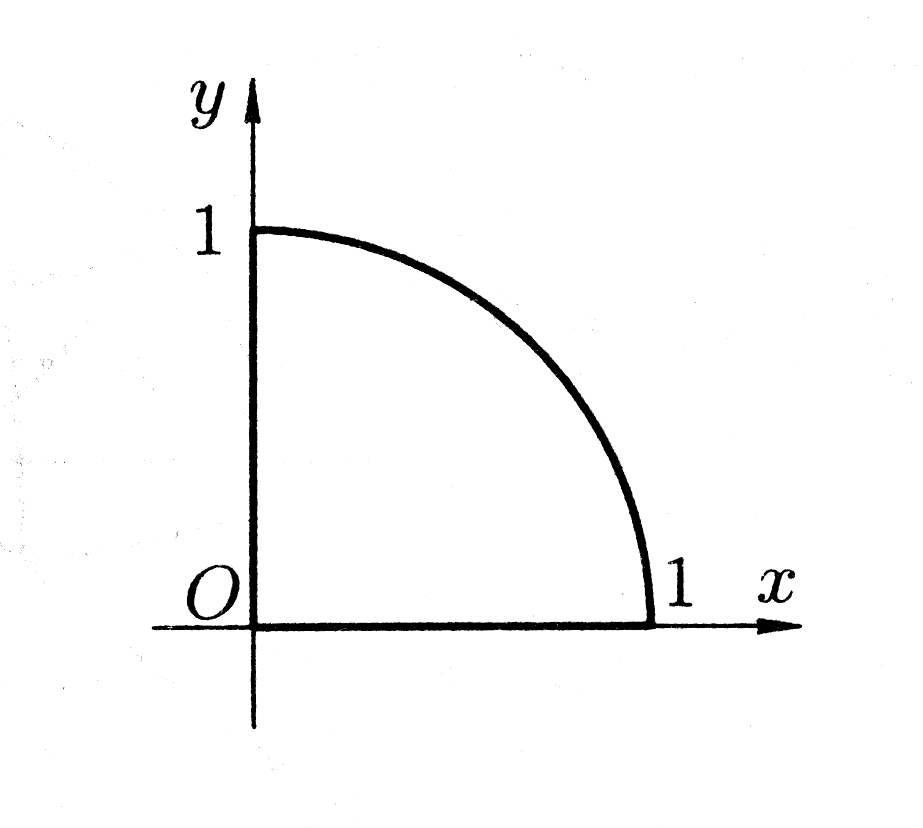
(рис. 25).
.
По названным поверхностям построим
чертеж области
(рис.24), а по соответствующим линиям –
область
.
(рис. 25).
Рис. 24. |
Рис. 25. |
Исходя
из вида подынтегральной функции и вида
области интегрирования, удобнее вычислять
интеграл в сферических координатах:
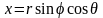 ,
,
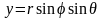 ,
,
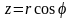 .
При этом
.
При этом
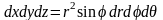 ,
,
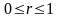 ,
,
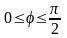 ,
,
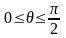 .
Подынтегральная функция равна
.
Подынтегральная функция равна
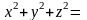
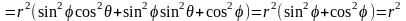
Таким образом,
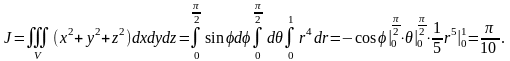
Пример
4.
Вычислить объем тела ограниченного
сферой
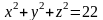 и поверхностью параболоида
и поверхностью параболоида
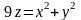 .
.
Тело
расположено над плоскостью
между полусферой
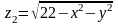 и параболоидом
и параболоидом
 (рис. 26).
(рис. 26).
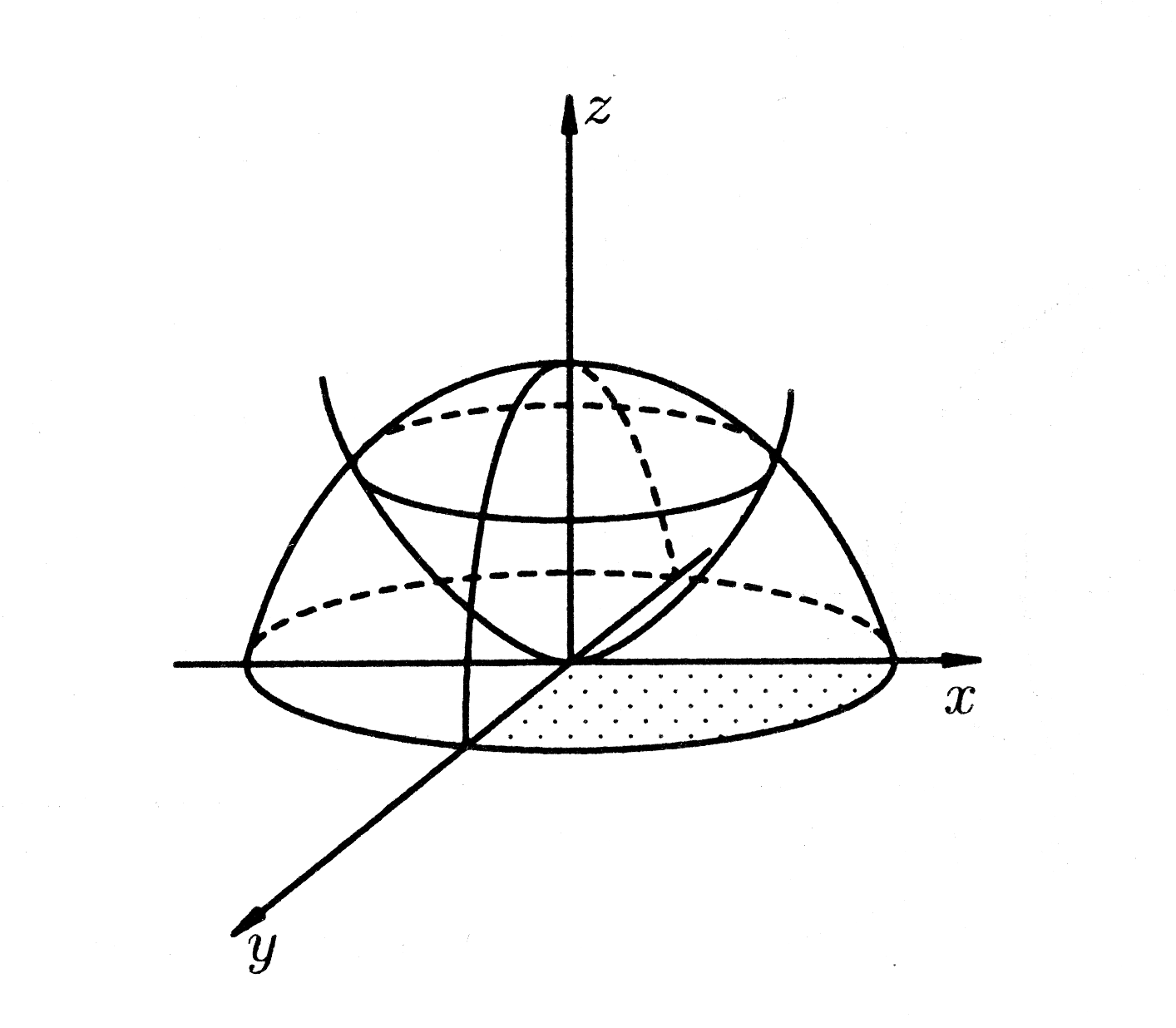
Рис. 26.
Объем тела вычислим по формуле
.
В силу симметрии тела относительно плоскостей и , переходим к цилиндрическим координатам , , и вычисляем объем четвертой части , а результат умножаем на 4.
 .
.
Для дальнейших вычислений надо найти область - проекцию на плоскость пространственной области . Для этого решим систему
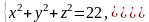

Подставляя
(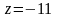 не подходит, т. к.
не подходит, т. к.
 )
во второе уравнение системы, найдем,
что сфера и параболоид пересекаются в
плоскости
по окружности
)
во второе уравнение системы, найдем,
что сфера и параболоид пересекаются в
плоскости
по окружности
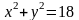 .
Следовательно, область
это четверть круга
.
Следовательно, область
это четверть круга
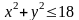 (
(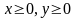 ),
или, в полярных координатах:
),
или, в полярных координатах:
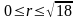 ,
.
Таким образом,
,
.
Таким образом,
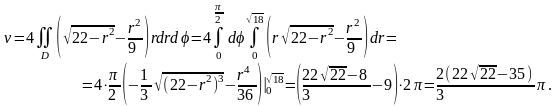
Пример
5.
Вычислить координаты центра тяжести
верхней половины шара радиуса
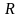 с центром в начале координат при условии,
что его плотность постоянна и равна
с центром в начале координат при условии,
что его плотность постоянна и равна
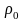 .
.
Сделаем сначала рисунок (рис. 27).
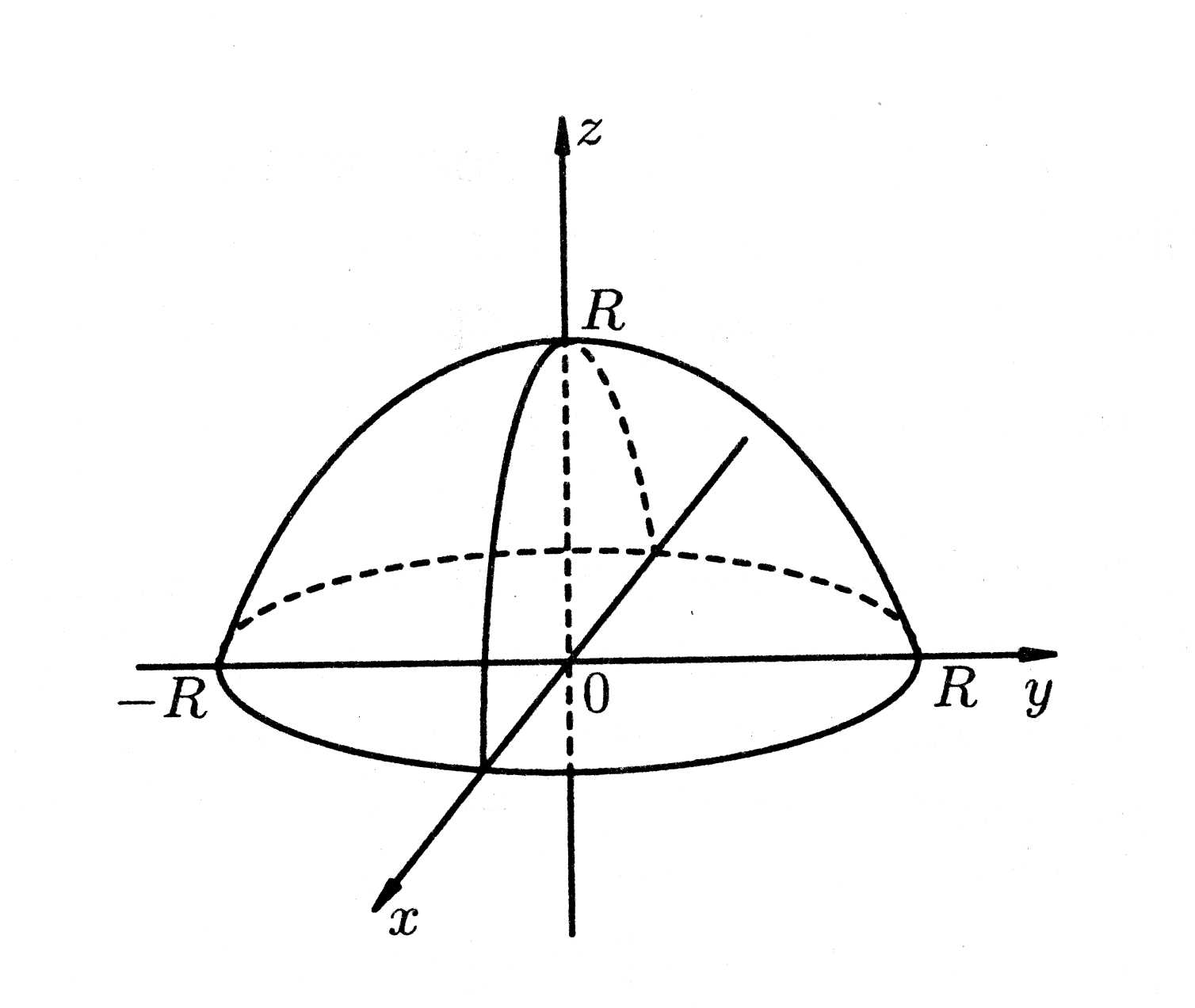
Рис. 27.
Воспользуемся формулами
, , ,
где
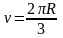 - объем полушара.
- объем полушара.
Подынтегральные
функции
и
в числителях первых двух дробей нечетные,
а область интегрирования
симметрична относительно соответствующих
плоскостей
и
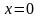 .
Поэтому
.
Поэтому
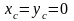 .
К этому же выводу приходим, исходя из
определения
.
К этому же выводу приходим, исходя из
определения
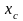 и
и
 и симметрии тела относительно координатных
плоскостей
и
.
Остается вычислить
и симметрии тела относительно координатных
плоскостей
и
.
Остается вычислить

Для этого переходим к сферическим координатам так же, как в примере 3. Получаем
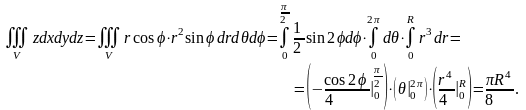
Следовательно,
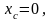
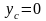 ,
,

Пример 6. Вычислить момент инерции прямого кругового цилиндра радиуса 4 и высоты 6 относительно диаметра сечения, проходящего через центр симметрии цилиндра; плотность цилиндра постоянна и равна .
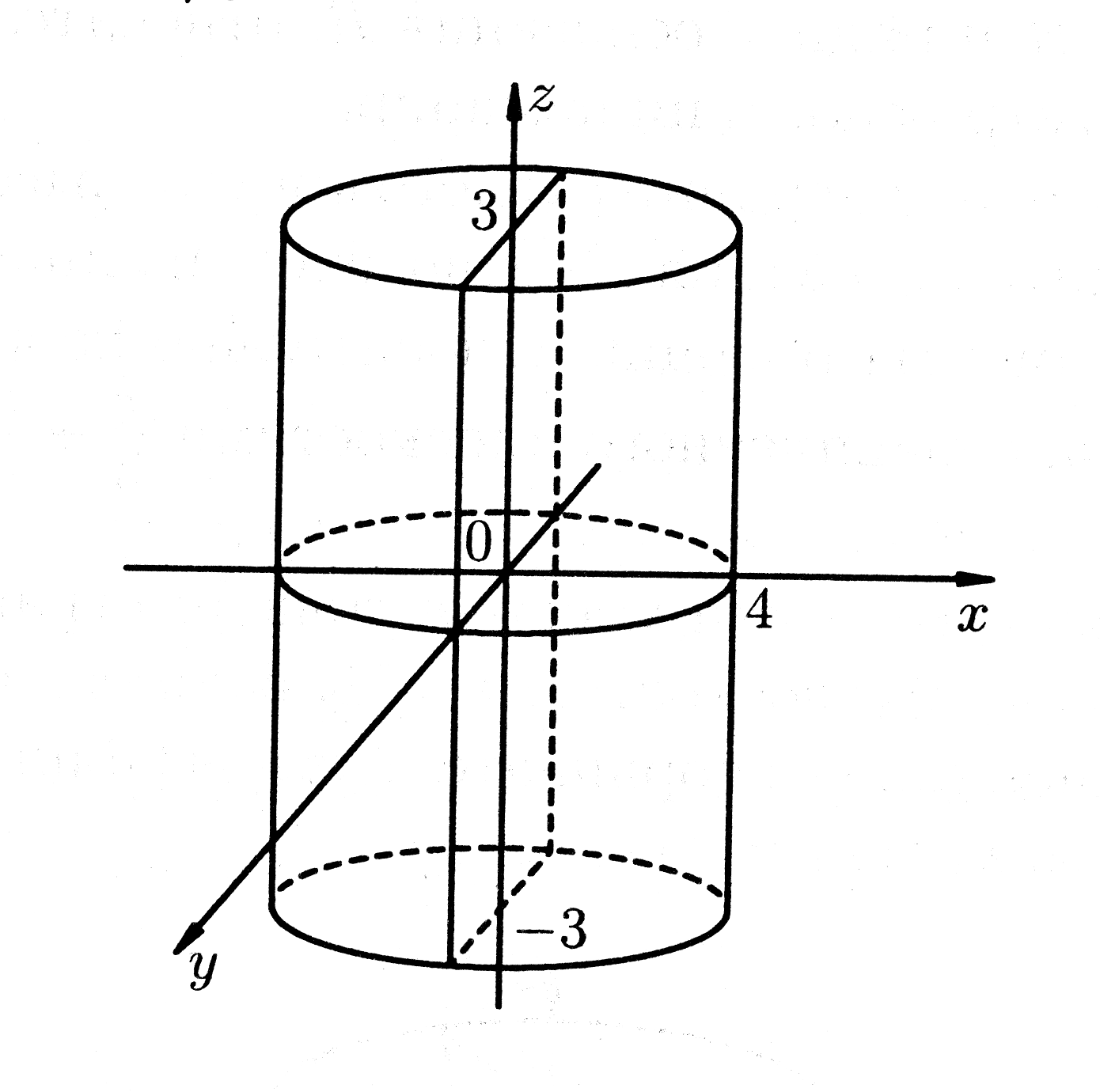
Рис. 28.
Введем
прямоугольную систему координат
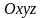 так, как обозначено на рис. 28: ось цилиндра
расположена на оси
,
среднее сечение цилиндра лежит в
плоскости
.
Тогда задача сводится к вычислению
- момента инерции цилиндра относительно
оси
.
Используем формулу
так, как обозначено на рис. 28: ось цилиндра
расположена на оси
,
среднее сечение цилиндра лежит в
плоскости
.
Тогда задача сводится к вычислению
- момента инерции цилиндра относительно
оси
.
Используем формулу
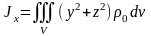 ,
,
где
- цилиндр:
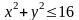 ,
,
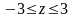 .
Перейдем цилиндрическим координатам:
,
,
,
.
Перейдем цилиндрическим координатам:
,
,
,
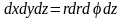 ,
,
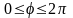 ,
,
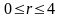 ,
.
Отсюда
,
.
Отсюда
 и, следовательно,
и, следовательно,
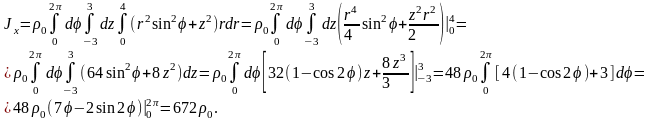
Пример
7.
Вычислить объем
и массу
тела
,
ограниченного конусом
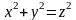 и плоскостью
и плоскостью
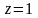 ,
если его плотность
,
если его плотность
 (x,
y,
z)
пропорциональна координате z
с коэффициентом пропорциональности k,
k>0.
(x,
y,
z)
пропорциональна координате z
с коэффициентом пропорциональности k,
k>0.
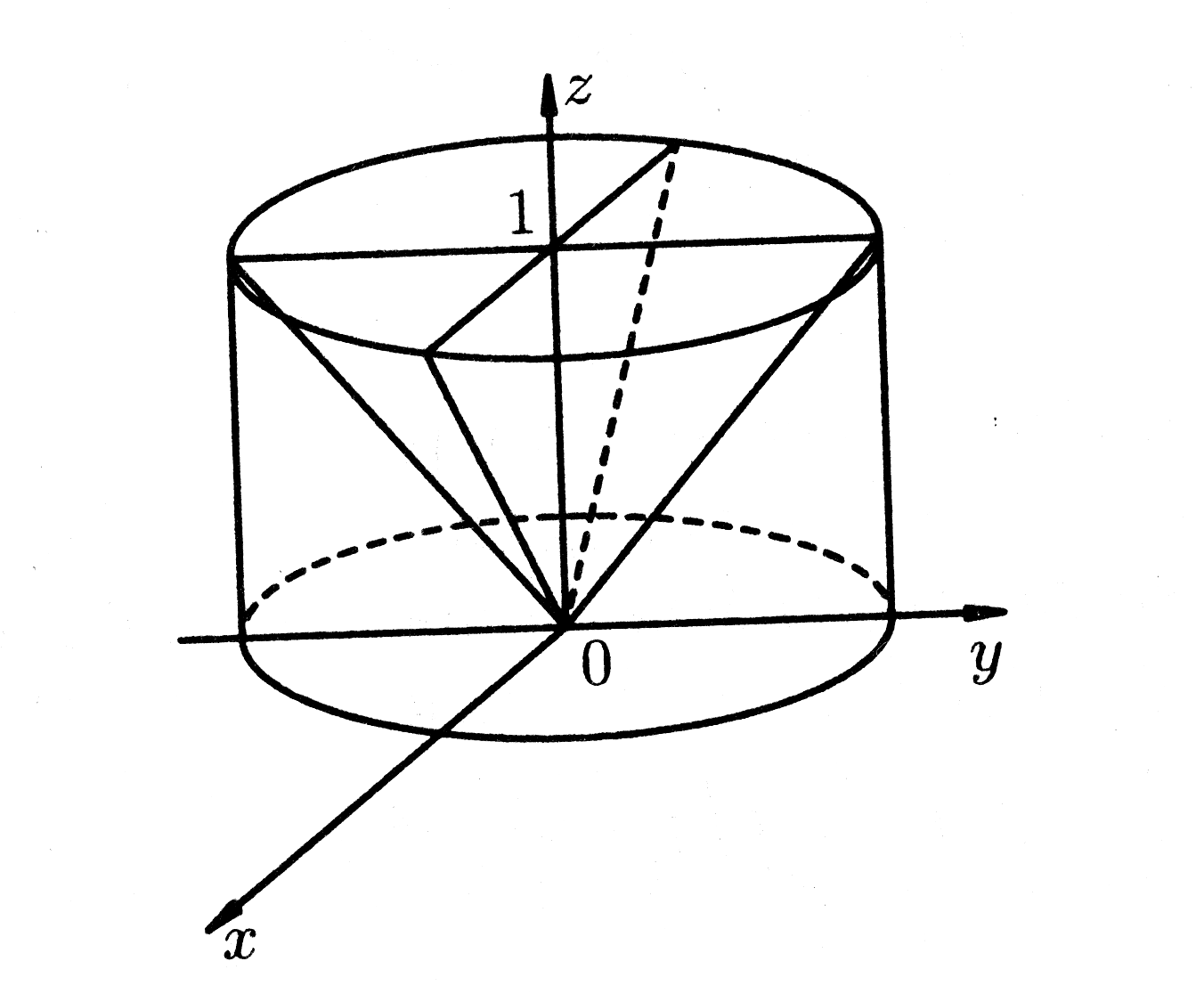
Рис. 29.
Требуемые
величины вычислим в цилиндрических
координатах:
,
,
,
,
,
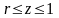 ,
(рис. 29):
,
(рис. 29):
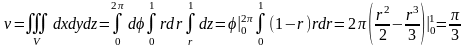 ;
;
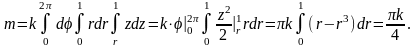
Контрольные вопросы:
Дайте определение тройного интеграла от функции по пространственной области.
Приведите формулу, по которой осуществляется переход к тройному интегралу в цилиндрических координатах.
Приведите формулу для вычисления тройного интеграла в сферических координатах.
По какой формуле находится объем тела?
Приведите формулу для вычисления массы тела с плотностью .
Приведите формулы для вычисления статических моментов тела , , относительно координатных плоскостей , , .
Приведите формулы для вычисления координат центра тяжести тела с массой т.
Приведите формулы для вычисления моментов инерции тела с плотностью относительно координатных плоскостей.