30 Кафедра математического анализа

Методические указания по математике для самостоятельной работы студентов специальности «Геология»

Глава 2. Кратные интегралы

§1. Двойной интеграл. Свойства и методы вычисления

Определение и геометрический смысл двойного интеграла

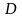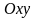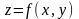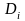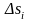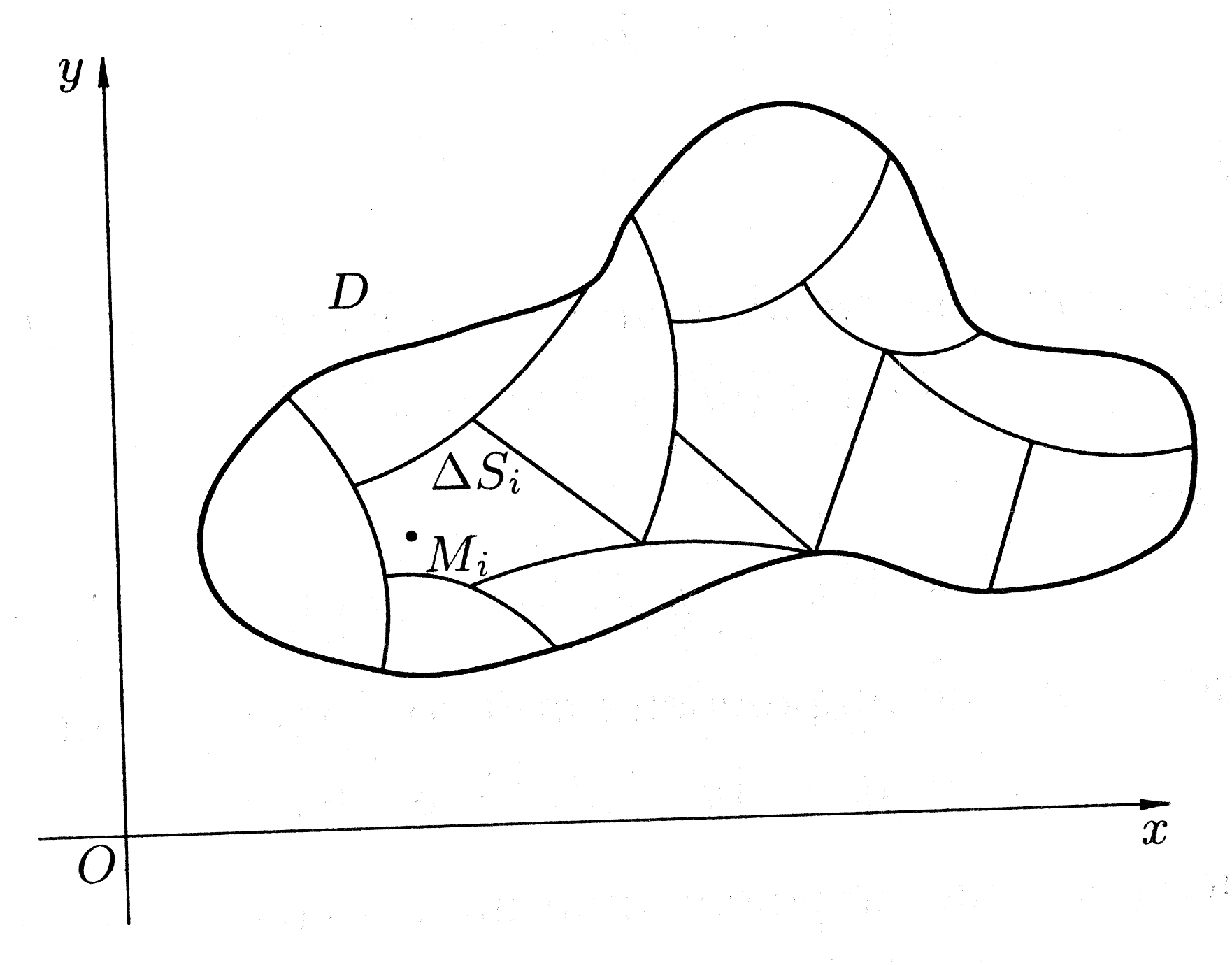
Пусть - некоторая замкнутая ограниченная область на плоскости , а - произвольная функция, определенная и ограниченная в этой области. Разобьем область произвольно на n непересекающихся частей , с площадями (i=1,2,…,n) (рис.1). В каждой части выберем произвольную точку 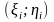и составим сумму

,

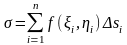которую назовем интегральной суммой для функци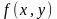и в области .

Error: Reference source not found

Рис. 1

Обозначим через d наибольшее расстояние между граничными точками области .

Если интегральная сумма при 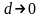имеет конечный предел, равный I, то этот предел называется двойным интегралом от функции по области и обозначается одним из следующих символов:

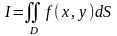; или .

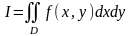Функция - интегрируемая в области , - область интегрирования, x и y – переменные интегрирования, ds (или dxdy) – элемент площади.

Если функция непрерывна в области , то она интегрируема.

Теорема 1. Если 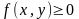и непрерывна в области , то интеграл

,

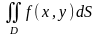выражает объем тела, ограниченного снизу областью , сверху – поверхностью , а с боков – цилиндрической поверхностью, образующие которой параллельны оси 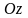, а направляющей служит граница области . (рис. 2).

В этом заключается геометрический смысл двойного интеграла.

Рис. 2.

В частности, если 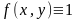, то равен площади области :

.

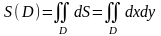Свойства двойного интеграла

1. Линейность. Если функции и 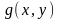непрерывны на области , то

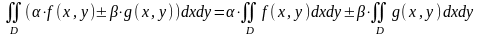
(α и β – постоянные числа).

2. Монотонность. Если функции и непрерывны на области и всюду в этой области 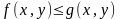, то

.

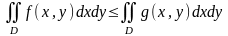Таким образом, неравенства можно почлено интегрировать.

В частности, если 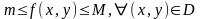, то

,

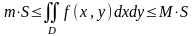где 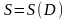- площадь области . Данные неравенства называются оценкой интеграла. Еще одно следствие: если на области , то

.

3. Теорема о среднем значении.

Если функция непрерывна на области , то существует точка 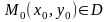такая, что

, или .

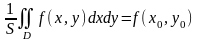При этом значение 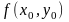, т. е. число

,

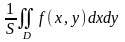называется интегральным средним значением функции в области .

4. Аддитивность. Если область представляется в виде объединения двух областе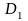й и 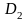без общих внутренних точек, то

.

5. Для любой функции , непрерывной на области , имеет место неравенство

.

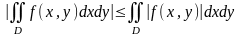Вычисление двойного интеграла

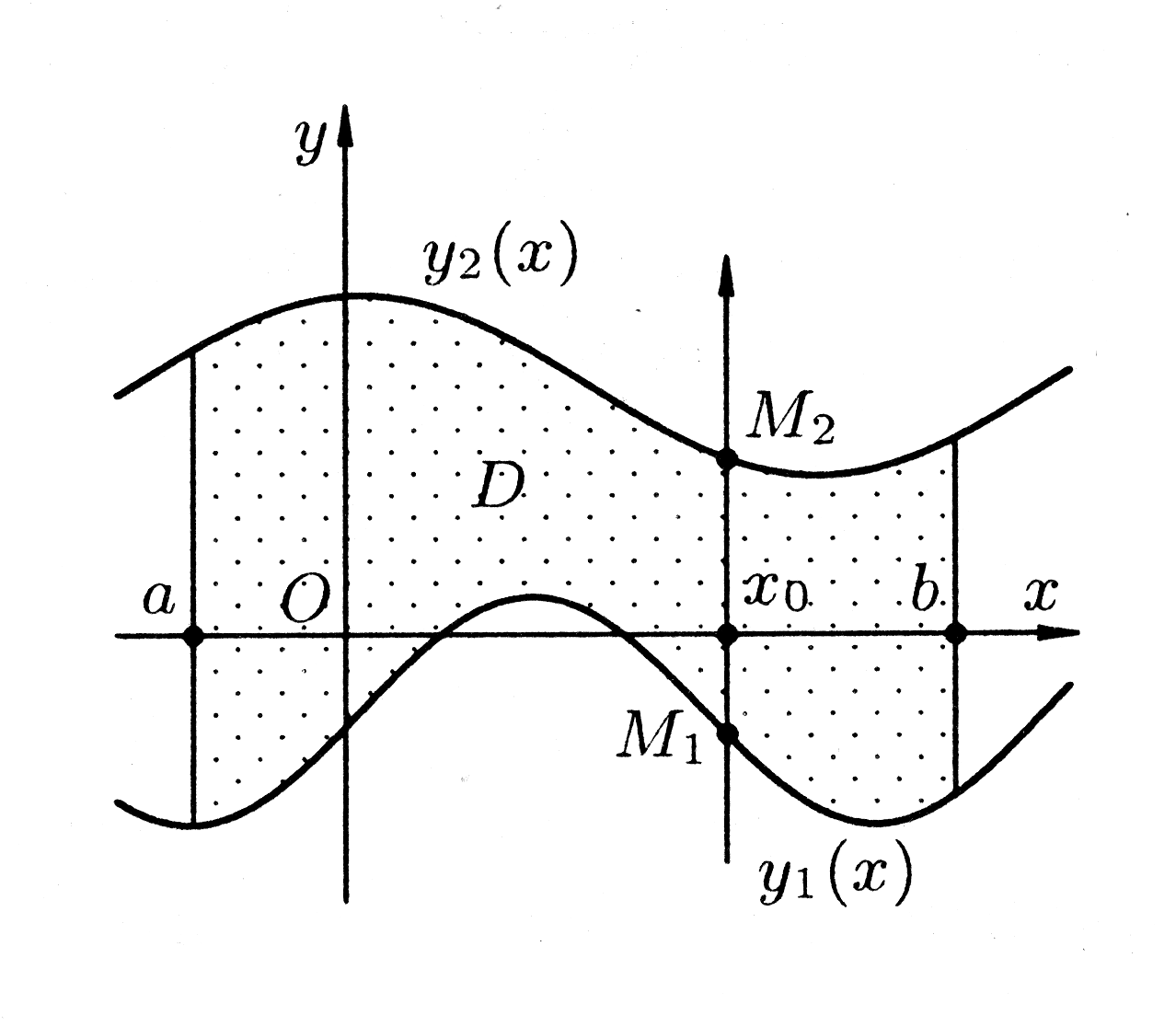
Предположим, что область можно задать в виде системы неравенств:

Геометрически это означает, что каждая вертикальная прямая пересекает границу области только в двух точках М₁ и М₂ (рис. 3), которые называются соответственно точкой входа и точкой выхода.

Тогда

.

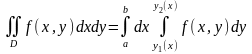Рис. 3.

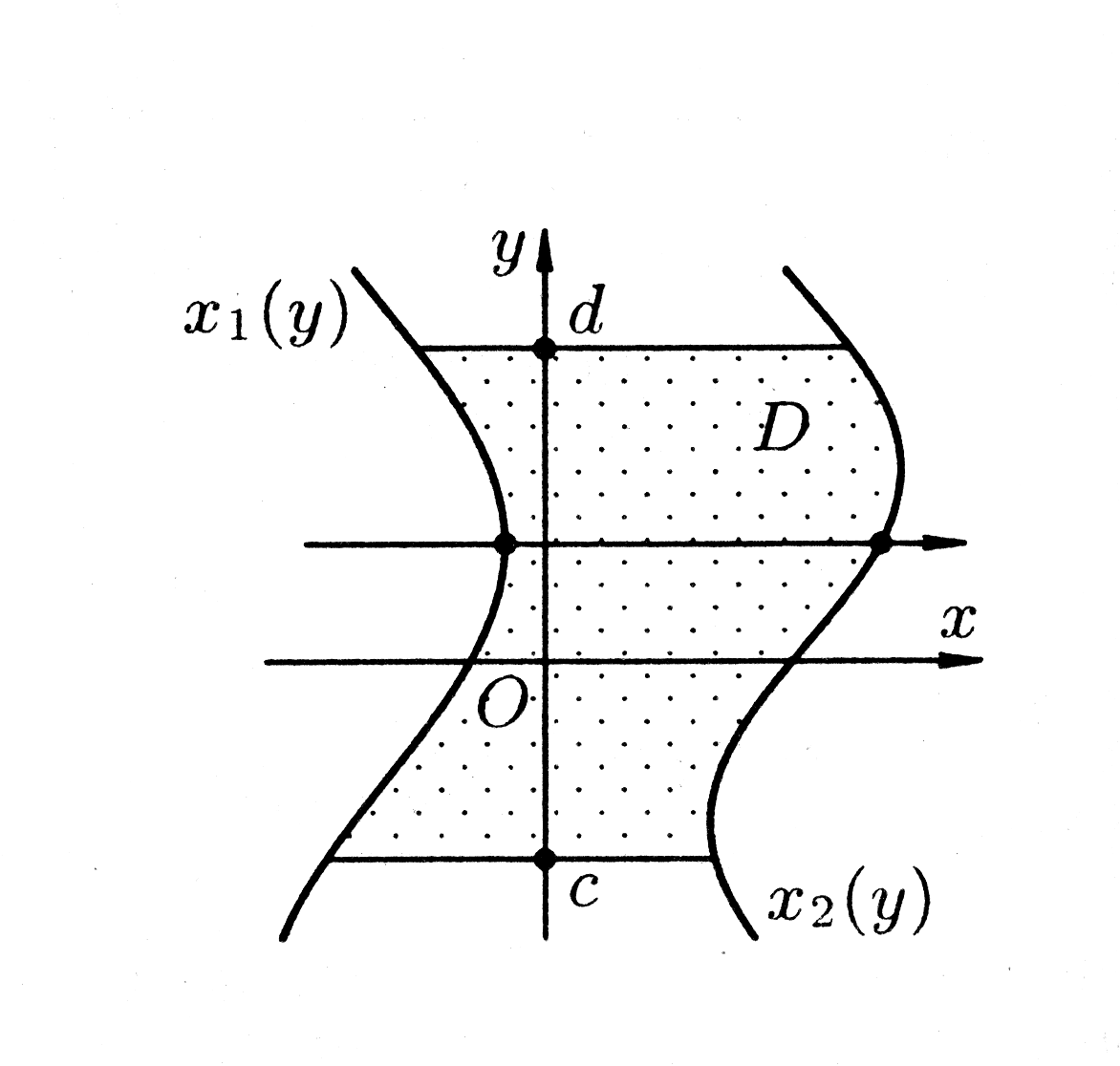
Рис. 4.

Если же область (рис.4) можно задать в виде системы неравенств:

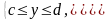
то

.

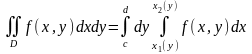Интегралы. стоящие в правых частях приведенных равенств, называются повторными. Они отличаются друг от друга порядком интегрирования. Интеграл, содержащий функцию , называется внутренним, другой – внешним. При вычислении повторных интегралов следует брать сначала внутренний интеграл, при этом переменная, не стоящая под знаком дифференциала, принимается постоянной. Затем вычисляется внешний интеграл. Каждый из них вычисляется при помощи формулы Ньютона – Лейбница, как определенный интеграл.

Области, не представимые в описанном выше виде, следует разбить на конечное число таких областей при помощи прямых, параллельных координатным осям (рис. 5). При вычислении двойных интегралов по таким областям следует применить свойство аддитивности.

Рис. 5.

Пример 1. Вычислить повторный интеграл .

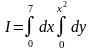Сначала вычислим внутренний интеграл по формуле Ньютона – Лейбница. Его результат будет подынтегральной функцией для внешнего интеграла.

.

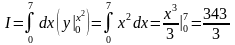Пример 2. Вычислить повторный интеграл .

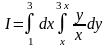Множитель 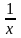(он не зависит от 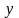, поэтому может считаться постоянным для внутреннего интеграла) можно вынести за знак интеграла, т. е. перенести во внешний интеграл:

.

Пример 3. Вычислить двойной интеграл , где - прямоугольник , .

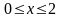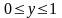Преобразуем двойной интеграл в повторный. Пределы интегрирования известны, поэтому

.

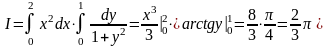Повторный интеграл свелся к произведению двух независимых друг от друга интегралов, поскольку результат вычисления внутреннего интеграла есть число.

Пример 4. Вычислить интеграл 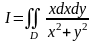, где область - параболический сегмент, ограниченный параболой и прямой .

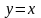Изобразим область интегрирования (рис.6). Так как прямая и парабола

пересекаются в точках 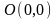и 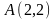, то область определяется системой неравенств

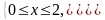
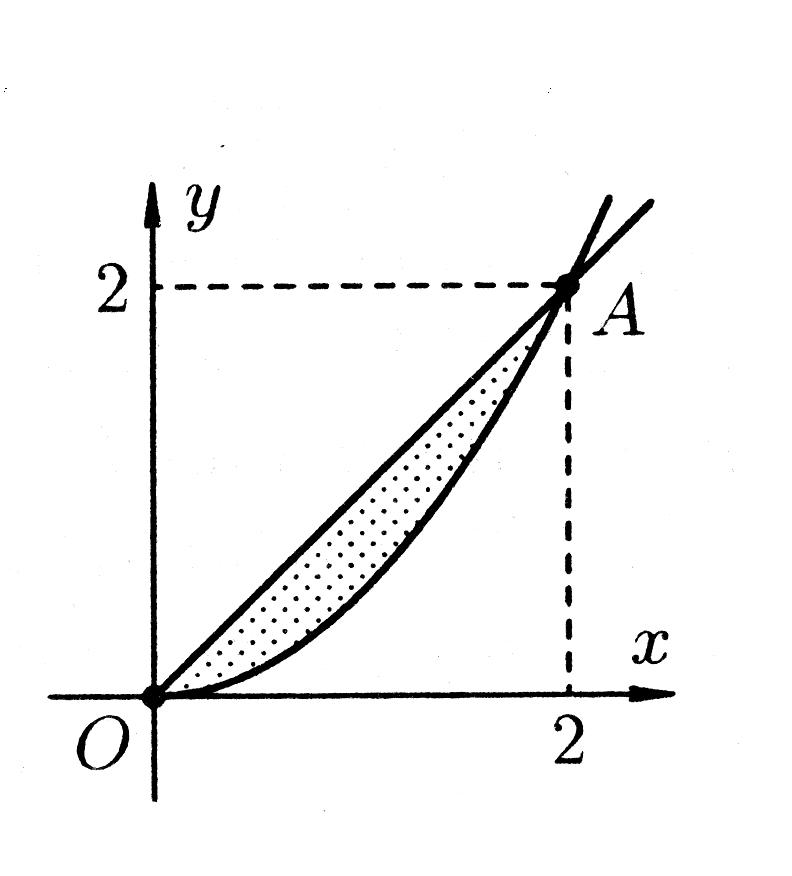
Рис. 6.

Теперь вычислим искомый интеграл :

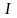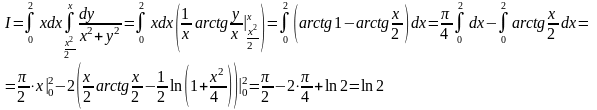
Пример 5. Вычислить интегральное среднее значение функци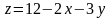и в области , ограниченной прямыми , .

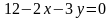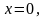
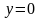Область - треугольник ОАВ, где , 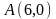, 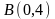- рис. 7.

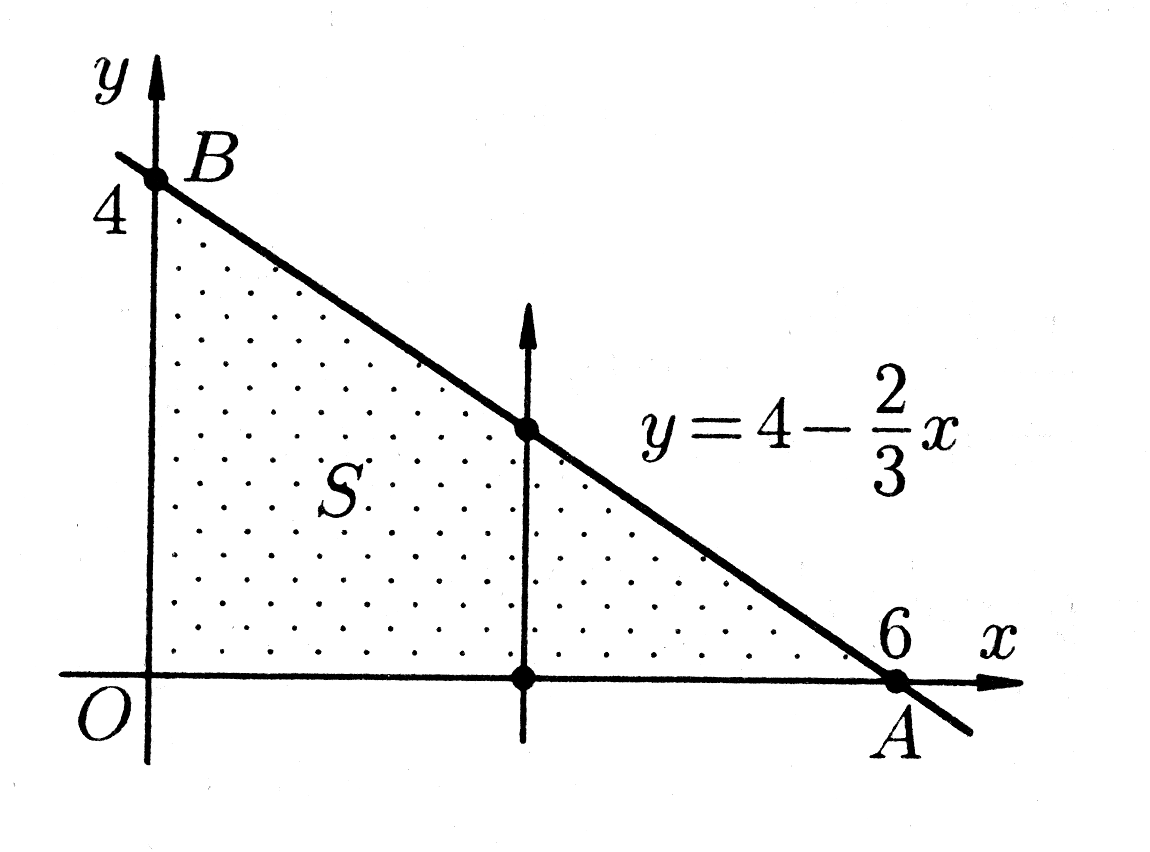
Рис. 7.

По определению интегральное среднее значение функции 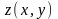в области равно 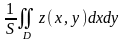, где S – площадь области (свойство 3).

Площадь S вычисляется по формуле площади прямоугольного треугольника: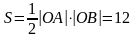 . Остается вычислить интеграл по области , которую можно задать неравенствами 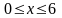, 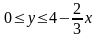.Имеем

Таким образом, искомое интегральное среднее равно 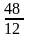, т. е. 4.

Контрольные вопросы:

1. Дайте определение интегральной суммы для функции в области D.

2. Что называется двойным интегралом от функции по области D?

3. В чем заключается геометрический смысл двойного интеграла?

4. Дайте определение интегрального среднего значения функции в области D?

5. Что называют повторными интегралами от функции по области D?