
- •30 Кафедра математического анализа
- •Глава 2. Кратные интегралы
- •§1. Двойной интеграл. Свойства и методы вычисления
- •§2. Замена переменных в двойном интеграле
- •§3. Применения двойного интеграла
- •§4 Тройной интеграл. Свойства, вычисление, применение
- •Вычисление тройного интеграла
- •Задания для самостоятельного решения:
§2. Замена переменных в двойном интеграле
Пусть функция непрерывна в некоторой замкнутой ограниченной области . Тогда для функции существует двойной интеграл
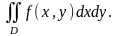
Предположим,
что с помощью формул
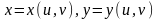 мы переходим к новым переменным
мы переходим к новым переменным
 и
и
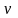 .
Переменные
.
Переменные
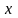 и
являются функциями непрерывными вместе
со своими частными производными первого
порядка по
и
в некоторой замкнутой области G
плоскости
и
являются функциями непрерывными вместе
со своими частными производными первого
порядка по
и
в некоторой замкнутой области G
плоскости
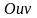 .
Предположим также, что эти функции
взаимно однозначно и непрерывно
отображают область G
на область
.
.
Предположим также, что эти функции
взаимно однозначно и непрерывно
отображают область G
на область
.
Тогда имеет место равенство
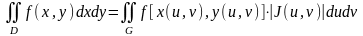 ,
где
,
где
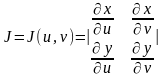 –
–
называется
якобианом
преобразования
G
в
(предполагается, что определитель
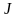 всюду отличен от нуля).
всюду отличен от нуля).
Координаты
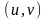 называются криволинейными
координатами
точки
называются криволинейными
координатами
точки
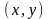 ,
поскольку уравнения
,
поскольку уравнения
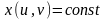 и
и
 представляют некоторые линии в области
G.
представляют некоторые линии в области
G.
Интеграл
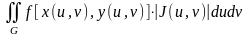
называется двойным интегралом в криволинейных координатах.
Простейшим
и важнейшим частным случаем криволинейных
координат являются полярные координаты
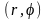 .
Они связаны с прямоугольными координатами
формулами
.
Они связаны с прямоугольными координатами
формулами
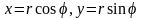
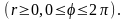 Якобиан преобразования в этом случае
равен
Якобиан преобразования в этом случае
равен
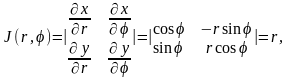
а
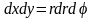 - элемент площади в полярных координатах.
- элемент площади в полярных координатах.
При этом имеет место формула замены переменных в двойном интеграле при переходе к полярным координатам
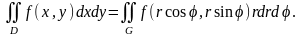
К полярным координатам особенно удобно переходить в тех случаях, когда область интегрирования круг или часть круга. Расстановка пределов и вычисление двойного интеграла в криволинейных координатах выполняется аналогично случаю прямоугольных координат.
Пример 1. Вычислить двойной интеграл
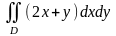
по
области
,
ограниченной прямыми
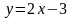 ,
,
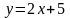 ,
,
 ,
,
 .
.
Область
- параллелограмм АВСК
(рис.8 а).
Хотя подынтегральная функция и область
интегрирования просты, вычисление
данного интеграла в прямоугольных
координатах достаточно громоздко.
Заметив, что уравнения прямых можно
записать в виде
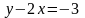 ,
,
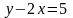 ,
,
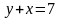 и
и
 ,
перейдем к новым координатам
,
перейдем к новым координатам
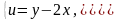 откуда
откуда
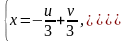
Имеем
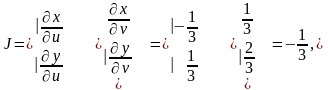
т.
е.
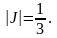 В новой системе координат (u,v)
область G
ограничена прямыми
В новой системе координат (u,v)
область G
ограничена прямыми
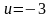 ,
,
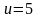 ,
,
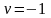 ,
,
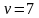 ,
т. е. представляет собой прямоугольник
(рис.8 б),
а подынтегральная функция равна
,
т. е. представляет собой прямоугольник
(рис.8 б),
а подынтегральная функция равна
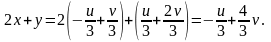
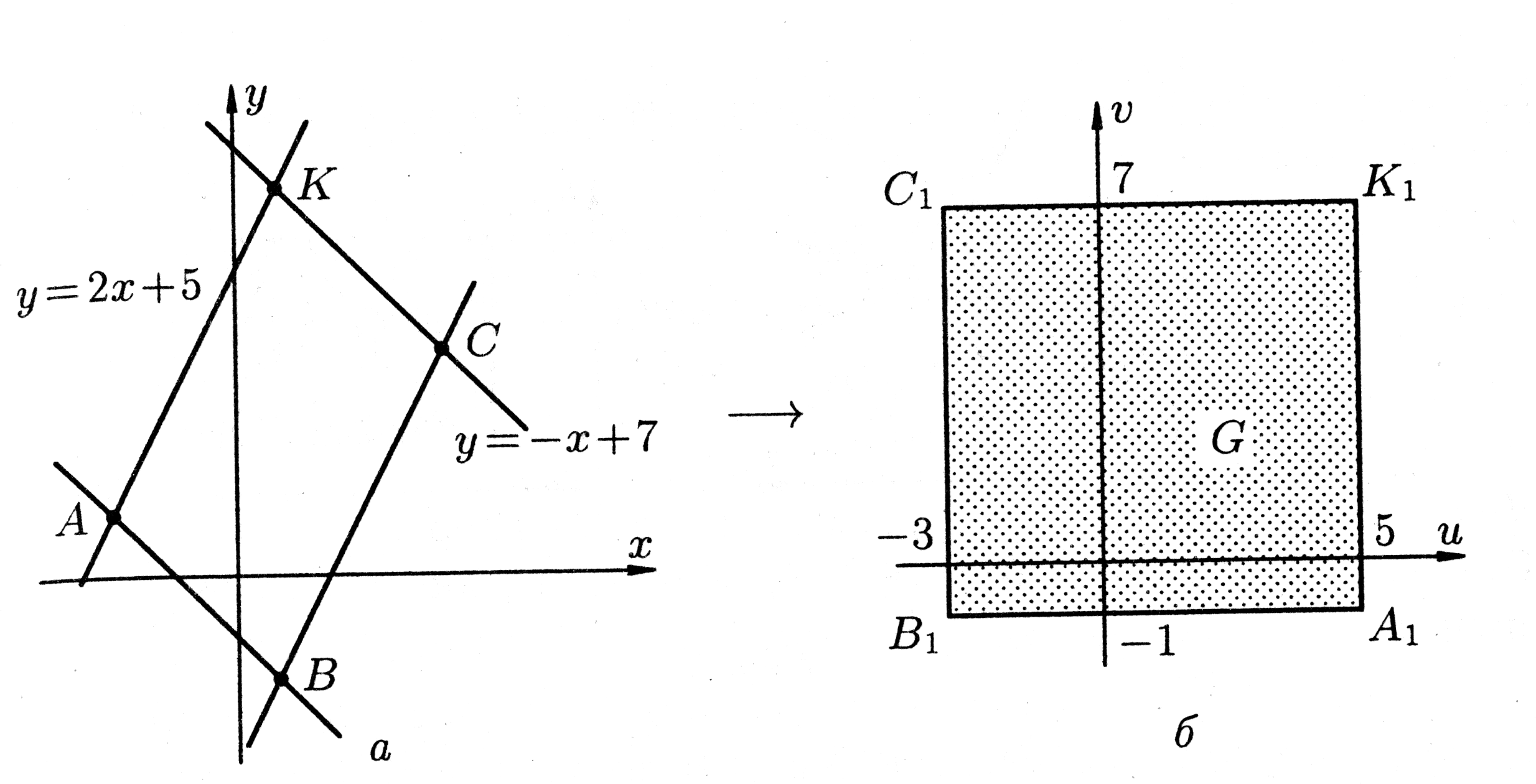
Рис.8.
Первая
система формул, написанная выше,
преобразует параллелограмм АВСК
в прямоугольник
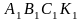 ,
вторая система – наоборот, преобразует
прямоугольник
в параллелограмм АВСК.
При этом видно, что направление обхода
вершин одной фигуры соответствует
противоположному направлению обхода
вершин другой. Именно поэтому J<0.
Переходим к вычислениям:
,
вторая система – наоборот, преобразует
прямоугольник
в параллелограмм АВСК.
При этом видно, что направление обхода
вершин одной фигуры соответствует
противоположному направлению обхода
вершин другой. Именно поэтому J<0.
Переходим к вычислениям:
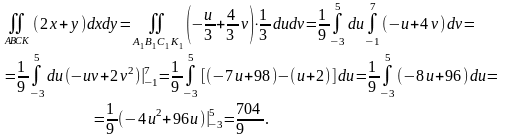
Пример 2. Вычислить
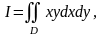
где
- область, ограниченная кривыми
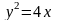 ,
,
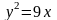 ,
,
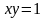 ,
,
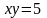 .
.
Область изображена на рис.9 а. Подходящая замена переменных позволяет свести этот интеграл к интегралу по прямоугольнику.
Введем
новые переменные
и
при помощи равенств
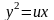 ,
,
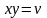 .
Выразим отсюда переменные
и
через
и
:
.
Выразим отсюда переменные
и
через
и
:
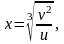
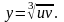

Рис. 9.
Находим якобиан полученного преобразования
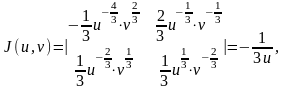
откуда,
с учетом того, что
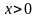 на области
,
а значит,
на области
,
а значит,
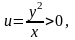 имеем
имеем
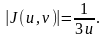
Таким образом, исходный интеграл в плоскости имеет вид
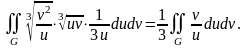
Граница
области G
описывается линиями
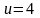 (так
как одна из формул преобразования имеет
вид
,
то линии
в плоскости соответствует линия
в плоскости
),
(так
как одна из формул преобразования имеет
вид
,
то линии
в плоскости соответствует линия
в плоскости
),
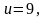

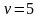 (рис. 9 б).
(рис. 9 б).
Поэтому
область G
имеет вид
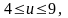
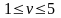 ,
а преобразованный интеграл вычисляется
проще:
,
а преобразованный интеграл вычисляется
проще:
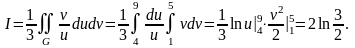
Пример 3. Вычислить интеграл
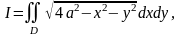
где
- круг
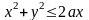 .
.
Строим
круг
радиуса
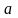 с центром в точке
с центром в точке
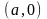 (рис.10). Подынтегральная функция четная
по переменной
,
а область интегрирования симметрична
относительно оси
(рис.10). Подынтегральная функция четная
по переменной
,
а область интегрирования симметрична
относительно оси
 Поэтому можно вычислить интеграл только
по верхнему полукругу и результат
удвоить:
Поэтому можно вычислить интеграл только
по верхнему полукругу и результат
удвоить:
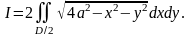
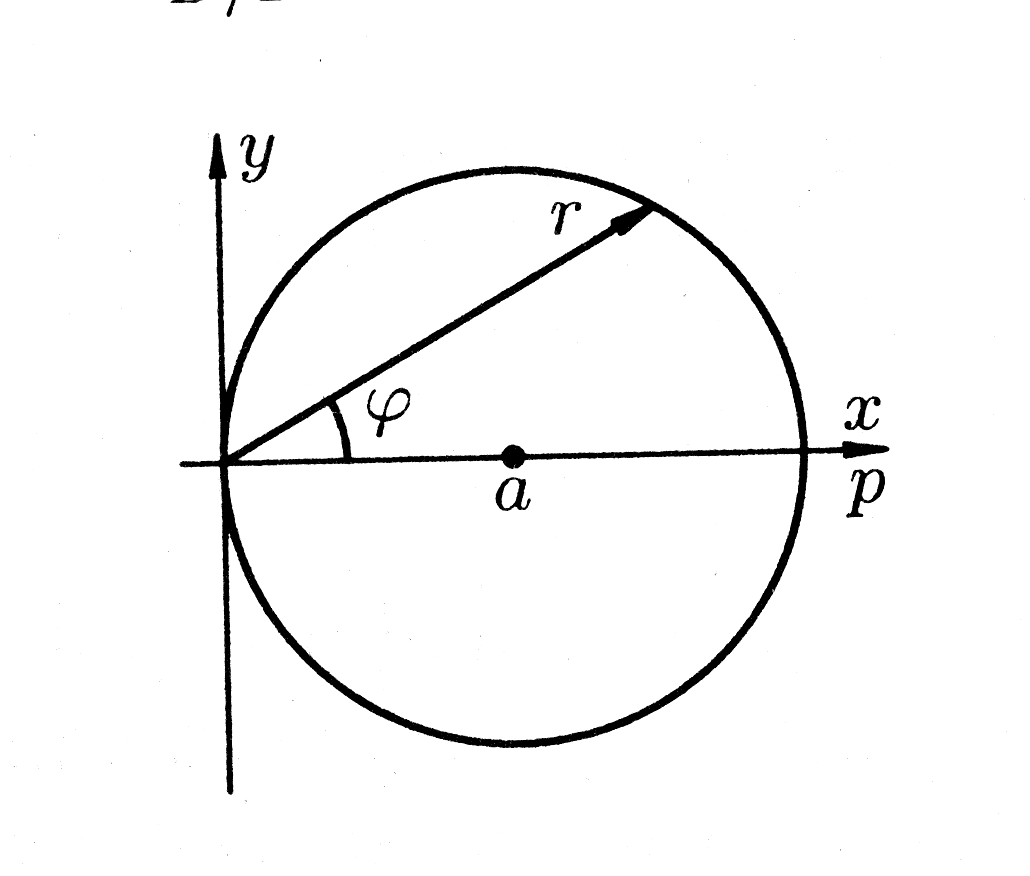 Рис. 10.
Рис. 10.
Переходим
к полярным координатам
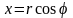 ,
,
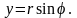 Для удобства расстановки пределов в
полярных координатах совместим полярную
систему с прямоугольной так, как это
показано на рис. 10. Тогда полукруг
Для удобства расстановки пределов в
полярных координатах совместим полярную
систему с прямоугольной так, как это
показано на рис. 10. Тогда полукруг
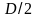 в полярных координатах задается системой
неравенств
в полярных координатах задается системой
неравенств
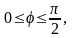
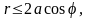 подынтегральная функция примет вид
подынтегральная функция примет вид
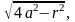 а
а
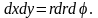 Таким образом,
Таким образом,
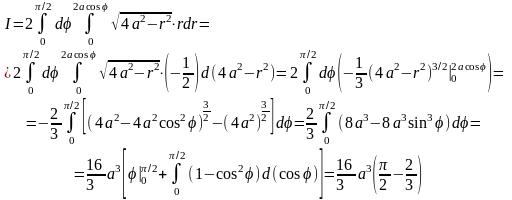
Пример
4. Вычислить
повторный интеграл
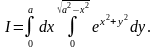
Сначала преобразуем повторный интеграл в двойной:
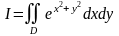 ,
где
,
где
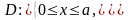
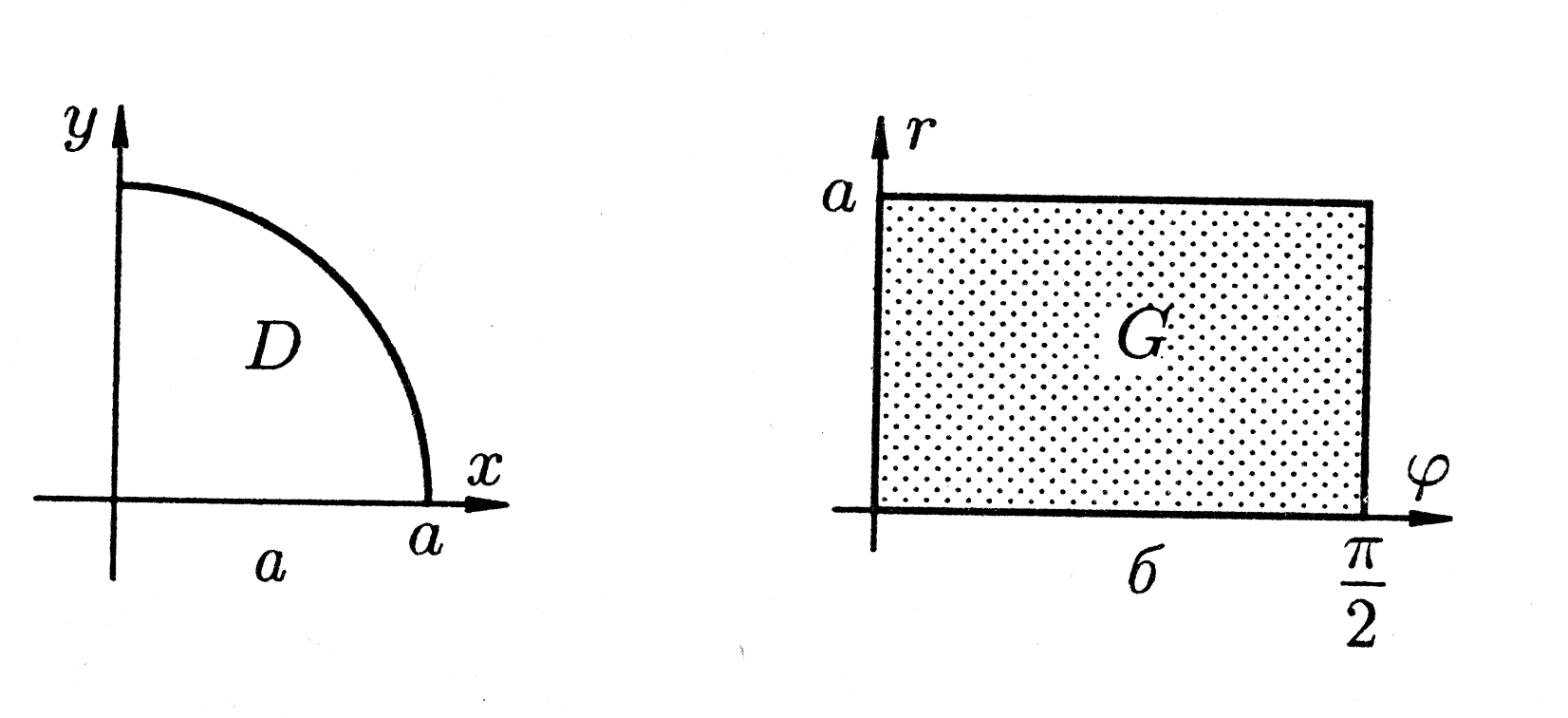
Рис. 11.
Область
интегрирования представляет собой
четверть круга (рис.11 а),
поэтому удобно перейти к полярным
координатам
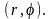 Полярную систему координат изобразим
также в виде прямоугольной (рис. 11 б).
Тогда область G
в системе координат
Полярную систему координат изобразим
также в виде прямоугольной (рис. 11 б).
Тогда область G
в системе координат
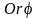 определяется системой неравенств
определяется системой неравенств
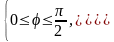
т.е.
G
– прямоугольник. Подынтегральная
функция имеет вид
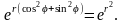 Следовательно,
Следовательно,

Пример 5. Вычислить
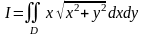 ,
,
где - область, ограниченная лемнискатой
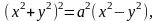
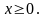
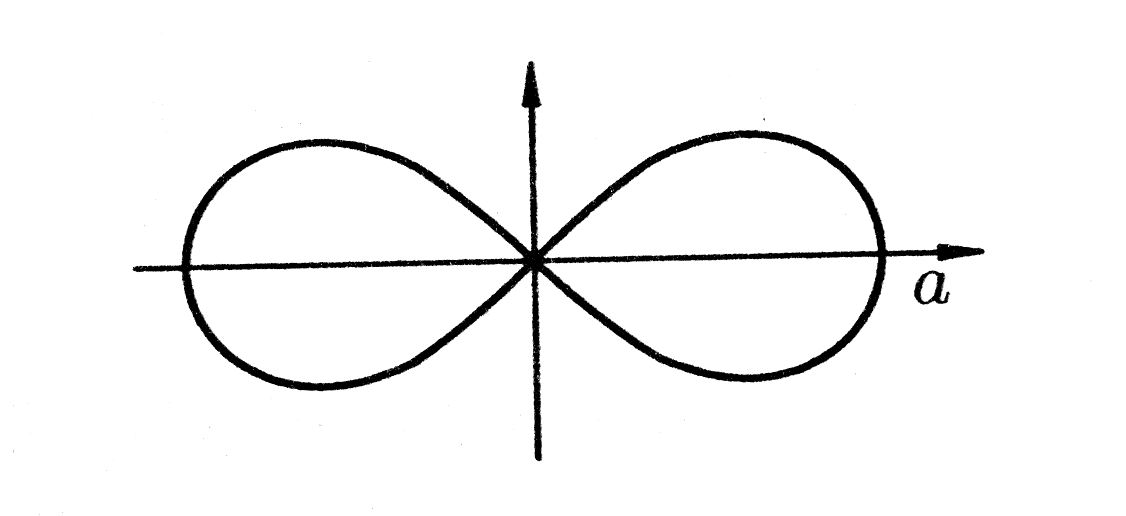
Рис. 12.
Заменяя
на
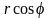 ,
а
на
,
а
на
 ,
получим уравнение лемнискаты (рис. 12) в
полярных координатах
,
получим уравнение лемнискаты (рис. 12) в
полярных координатах
 (
(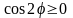 при
при
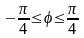 ).
Подынтегральная функция равна
).
Подынтегральная функция равна
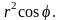 В силу симметрии лемнискаты относительно
оси
В силу симметрии лемнискаты относительно
оси
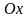 и четности подынтегральной функции
относительно переменной
можно записать:
и четности подынтегральной функции
относительно переменной
можно записать:
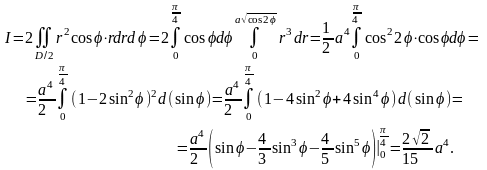
Контрольные вопросы:
Дайте определение якобиана преобразования G в D.
Что называется двойным интегралом в криволинейных координатах?
Чему равен якобиан преобразования в случае полярных координат?
В каком случае при вычислении двойного интеграла удобно переходить к полярным координатам?
