7 Подготовка системы дифференциальных уравнений к выполнению
интегрирования
Формирование
системы дифференциальных уравнений
для их решения рекомендуется осуществлять
в матричном виде. Для этого необходимо
составить матрицу Якоби и вектор внешних
воздействий. Примем во внимание, что
искомыми фазовыми координатами в системе
дифференциальных уравнений (27) являются
скорости подрессоренных и неподрессоренных
масс
,
и водителя
(или пассажира), а также усилия упругих
элементов подвески
,
шин
и сиденья
.
Следовательно, размерность матрицы
Якоби системы уравнений будет
.
Выполним необходимые преобразования исходной системы уравнений (27). Для этого подставим в нее значения потенциалов диссипативных элементов из компонентных уравнений (28). В результате система дифференциальных уравнений (27) получает следующий вид:
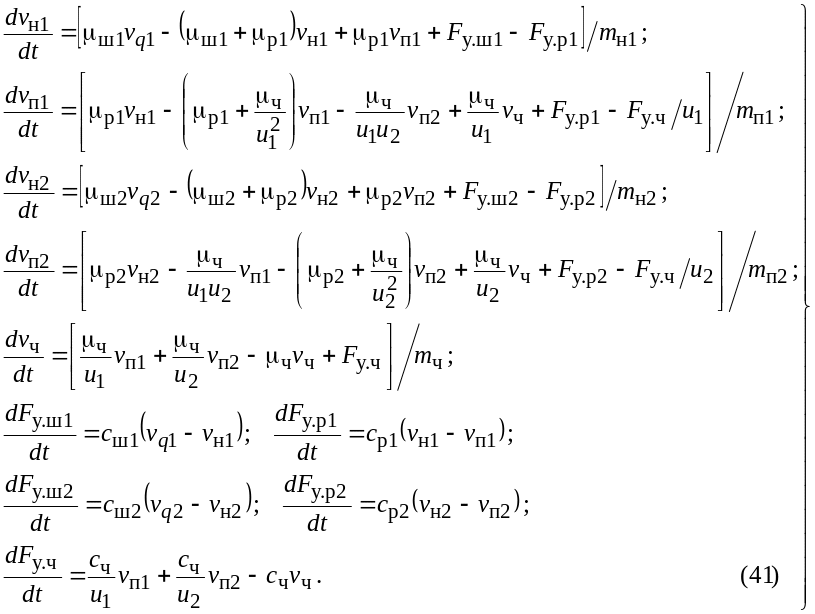
На основе
преобразованной системы дифференциальных
уравнений (41) составляется матрица Якоби
и вектор внешних воздействий
.
Выражения для вычисления элементов
матрицы Якоби
приведены в таблице 3.
Таблица 3 – Матрица Якоби системы дифференциальных уравнений
|
|
|
|
|
|
1 |
|
|
0 |
0 |
0 |
2 |
|
|
0 |
|
|
3 |
0 |
0 |
|
|
0 |
4 |
0 |
|
|
|
|
5 |
0 |
|
0 |
|
|
6 |
|
0 |
0 |
0 |
0 |
7 |
|
|
0 |
0 |
0 |
8 |
0 |
0 |
|
0 |
0 |
9 |
0 |
0 |
|
|
0 |
10 |
0 |
|
0 |
|
|
Продолжение таблицы 3
|
|
|
|
|
|
1 |
|
|
0 |
0 |
0 |
2 |
0 |
|
0 |
|
|
3 |
0 |
0 |
|
|
0 |
4 |
0 |
0 |
0 |
|
|
5 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
0 |
0 |
10 |
0 |
0 |
0 |
0 |
0 |
На основе выражений,
приведенных в таблице 3, необходимо
вычислить элементы матрицы Якоби
и свести их численные значения в
аналогичную таблицу.
Для вычисления
элементов вектора внешних воздействий
,
согласно уравнениям (27), используются
следующие выражения:
(42)
На основе матрицы Якоби определяются ее собственные значения (спектр матрицы Якоби), которые позволяют оценить устойчивость моделируемой системы и определить ее резонансные частоты. Результаты вычислений собственных значений матрицы Якоби необходимо свести в таблицу и дать оценку физических свойств моделируемой системы.
При составлении
компьютерной программы для интегрирования
системы дифференциальных уравнений
(41) целесообразно ввести обозначение
вектора фазовых координат
,
и элементов этого вектора:
;
;
;
;
;
;
;
;
.
Система дифференциальных уравнений при этом может быть представлена в следующем виде:
(43)
Матричная форма системы дифференциальных уравнений (43) позволяет составить компактную компьютерную программу для их решения.
Так как начало
отсчета фазовых координат принято в
положении статического равновесия
динамической системы, то начальные
условия интегрирования будут нулевые,
т.е.
.
Порядок системы уравнений (41)
.