2.2.3. Первая задача Циолковского

Рассмотрим движение ракеты в безвоздушном пространстве при отсутствии гравитационного поля. Движение в этом случае будет происходить только под действием реактивной силы.

Какую скорость V приобретет ракета к моменту, когда на­чальная масса М₀ уменьшится до конечного значения М_к (до пол­ной выработки топлива)? Это – первая задача Циолковского.

Запишем уравнение Мещерского:

.

После разделения переменных получим:

.

Т.к. , после интегрирования получим:

.

Значение С получим из начальных условий: при t = 0 скорость V = V₀ =0 и масса М = М₀.

Тогда: .

­Откуда: .

Подставив С в выражение для V, окончательно получим:

. (2.20)

где: М – текущая масса ракеты;

– относительная текущая масса ракеты.

Это формула Циолковского для определения идеальной скорости одноступенчатой ракеты, которая характеризует энергетические ха­рактеристики собственно ракеты.

По мере выработки топлива масса М и соответственно  уменьшаются, а скорость V – возрастает.

В частности, при значении скорость V ракеты всегда равна эффективной скорости w_e истечения (см. рис. 2.6).

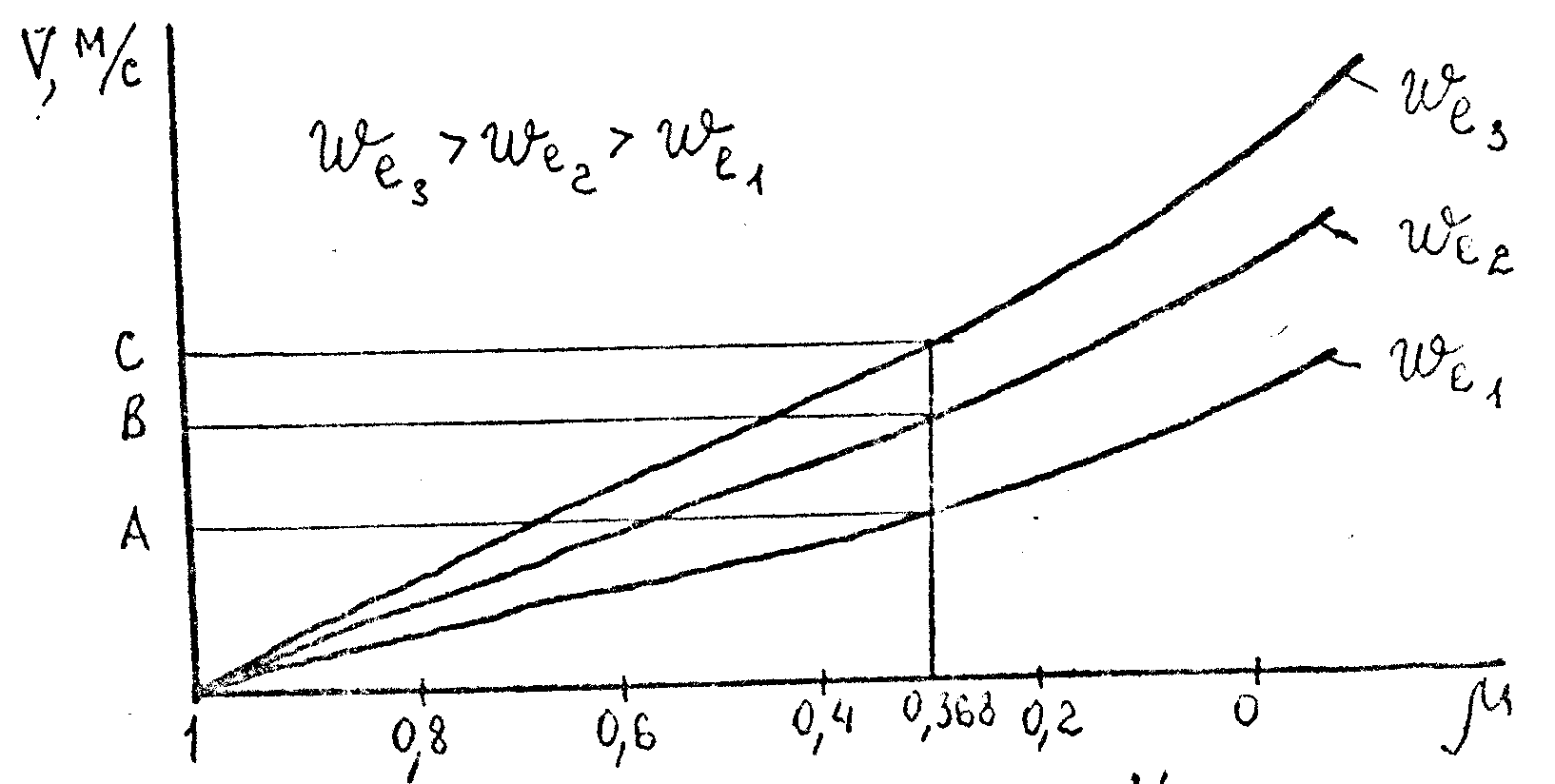
Рис. 2.6. Изменение скорости V в зависимости от  для различных w_e

Когда топливо будет полностью выработано, а двигатель выключен, скорость V достигнет своего наибольшего конечного V_к значения:

, (2.21)

где: – относительная конечная масса;

M_к , M₀ – конечная и начальная масса ракеты соответственно;

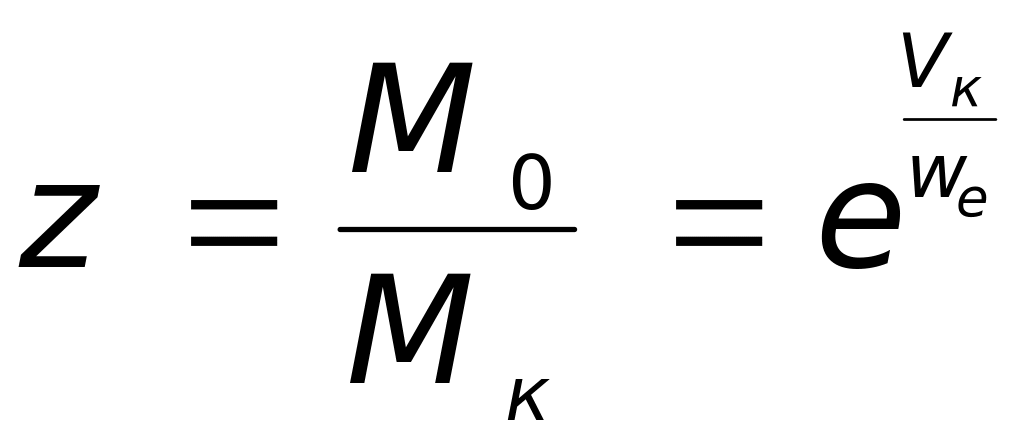– число Циолковского.

Другая форма записи конечной скорости:

где: М_Т – масса топлива;

– относительная масса топлива.

Рассмотрим, от каких параметров зависит путь S_К, пройденный ракетой в идеальных условиях за время t_К .

Очевидно: .

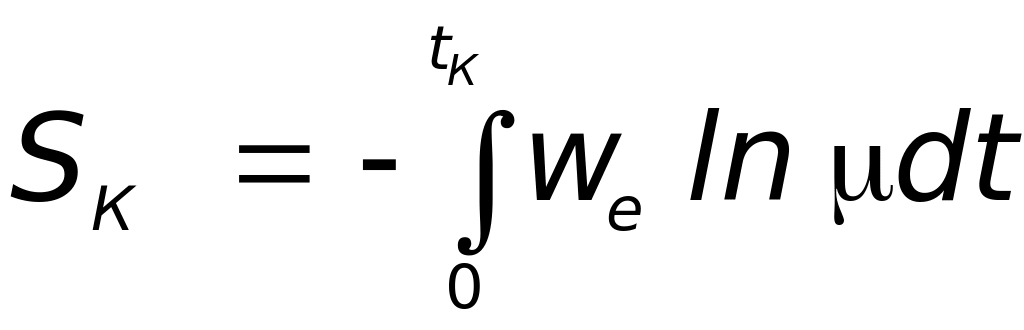При текущая масса М ракеты линейно зависит от времени:

.

Поэтому: .

Тогда после замены переменных:

,

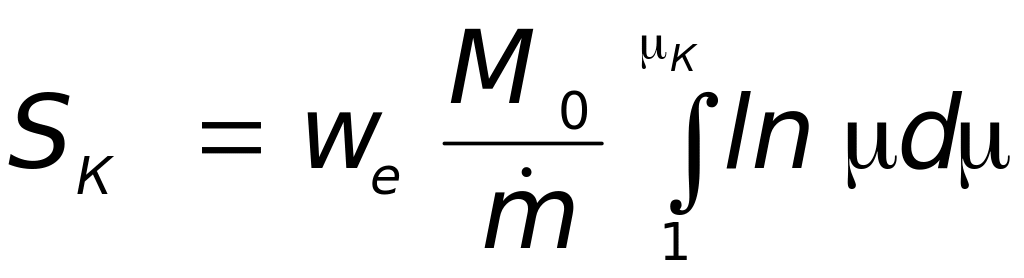или после интегрирования:

.

Так как:

,

то:

.

Поэтому:

, (2.22)

где: – стартовая нагрузка на тягу.

Величину, обратную ₀ называют тяговооруженностью :

. (2.23)

Выясним, какое влияние оказывает тяговооруженность на время t работы двигателя.

Выше отмечалось, что при линейном законе изменения массы ЛА:

и .

Откуда:

.

Учитывая, что :

,

или:

.

Из последних двух выражений следует, что для ракет с одинаковыми скоростями истечения равным значениям  может соответствовать разное время работы двигателя: чем больше начальная тяговооруженность , тем меньше время.

На рис. 2.7 дана зависимость V = f(t) для и различных, значений начальной тяговооруженности . Равные значения скорости, очевидно, имеют место при равные .

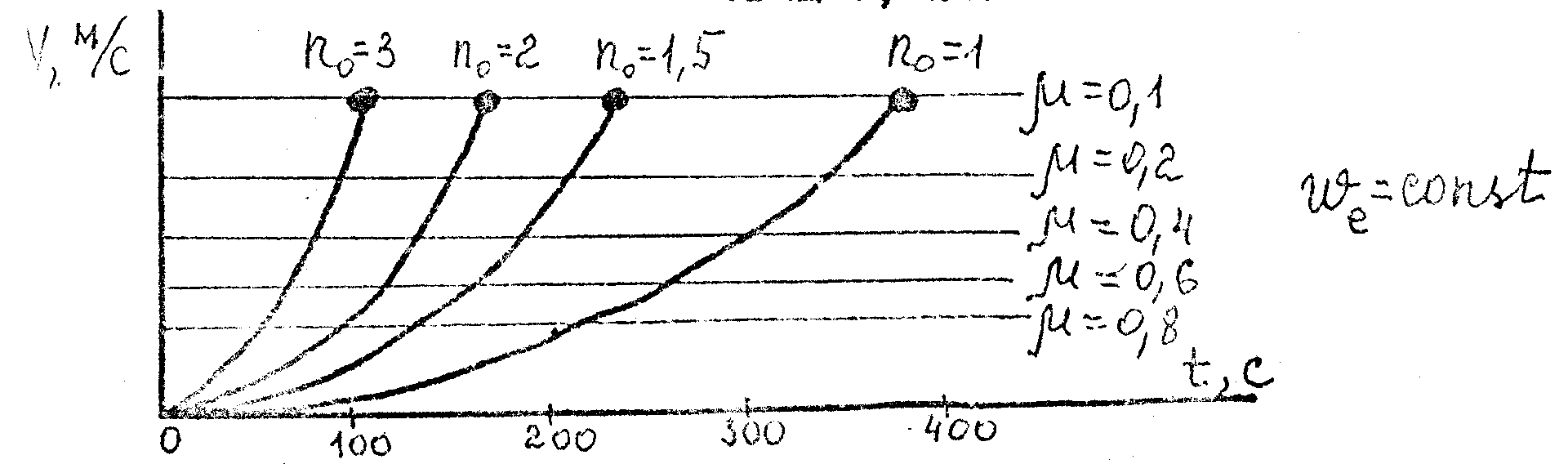
Рис. 2.7. Зависимость скорости V от времени t полета для различных значений начальной тяговоорукенности

Увеличение конечной идеальной скорости ракеты можно достичь либо увеличением эффективной скорость истечения продуктов сгорания, либо уменьшением относи­тельной конечной массы _К (увеличением числа Z Циолковско­го). Закон же расхода топлива, равно как и абсолютные зна­чения начальной и конечной масс, не оказывают влияния на приобретенную скорость.

Путь, проходимый ракетой, зависит не только от и но и обратно пропорционален тяговооруженности , т.е. стартовому ускорению. Этот факт объясняется тем, что с увеличением , уменьшается время t работы двигателя, а следовательно, снижаются гравитацион­ные потери скорости. В итоге это проводит к увеличению конечной скорости ракеты, движущейся в поле тя­готения планеты, а, следовательно, растет и проходимый ею путь.