2.1. Траектория полета ракеты-носителя

Траектория полета – путь, проходимый ракетой-носителем при выведении полезного груза на орбиту. Основные участки траектории полета ТКС см на рис. 2.1.

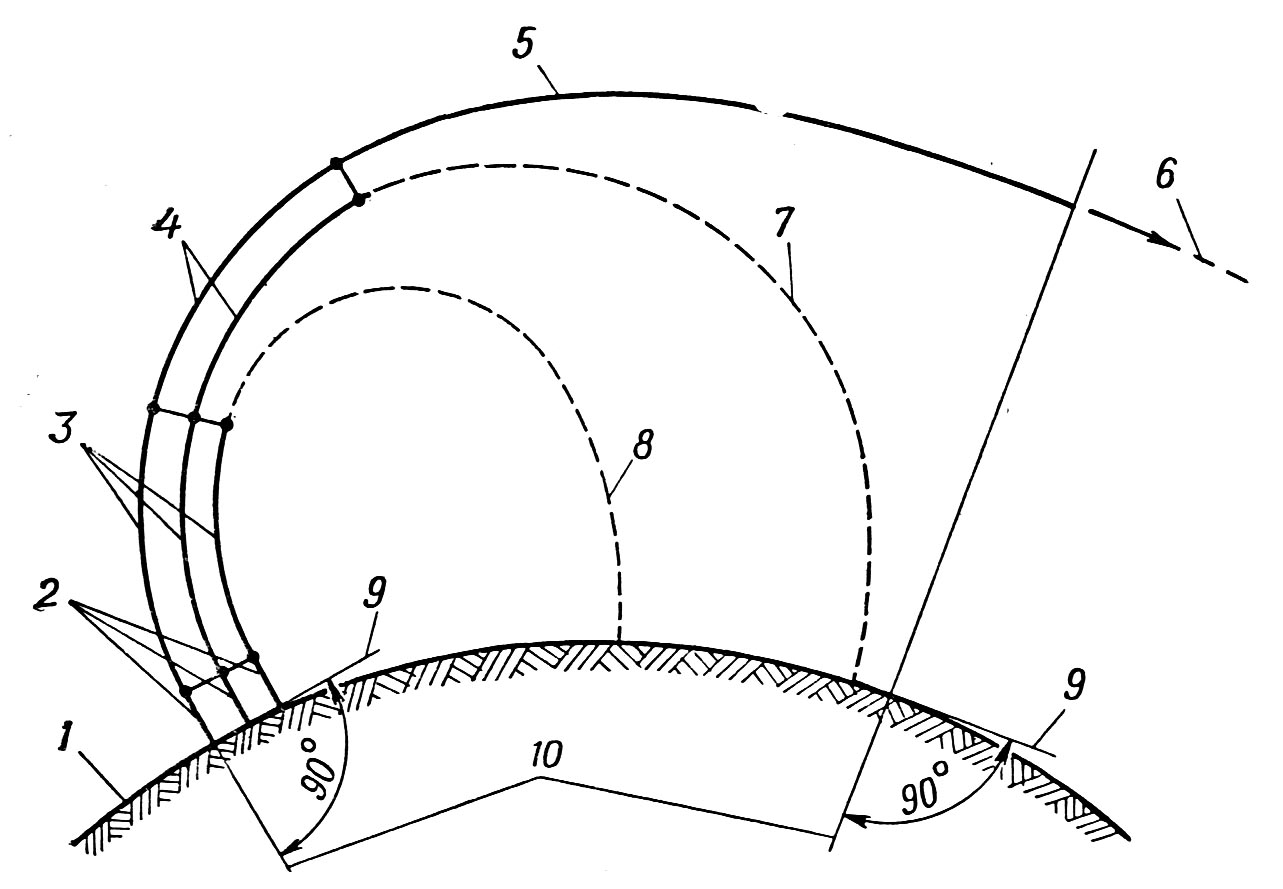
Рис. 2.1. Траектория ракеты-носителя

1 – Земля; 2 – вертикальный участок полета; 3 – активный участок полета 1-й ступени; 4 – активный участок полета 2-й ступени; 5 – активный участок полета 3-й ступени; 6 – орбита КА; 7 – пассивный участок полета ракетного блока 2-й ступени; 8 – пассивный участок полета ракетного блока 1-й ступени; 9 – местный горизонт; 10 – направление радиуса Земли

Активный участок полета – движение системы с работающими двигателями.

За вертикальным участком полета (2) следует программный разворот (3), в соответствии с задаваемой системой управления (СУ) программой выведения для решения требуемой целевой задачи.

Пассивный (свободный) участок полета по траектории (7, 8) или орбите (6). ЛА или отработавшие ракетные блоки (РБ) совершают полет, как свободно брошенное тело.

Ракета-носитель служит для выведения на опорную орбиту космического аппарата (КА).

Орбита космического аппарата – путь КА в поле центральной силы, определяемый воздействием силы тяготения (космический аппарат считается бесконечно малым телом, масса его мала по сравнению с массой цент­рального тела, что его можно считать притягиваемым централь­ным телом, но не притягивающим последнее).

Поле притягива­ющей силы – поле тяготения, создавае­мое однородным и сферическим телом (применительно к ИСЗ – Земля с ее полем тяготения).

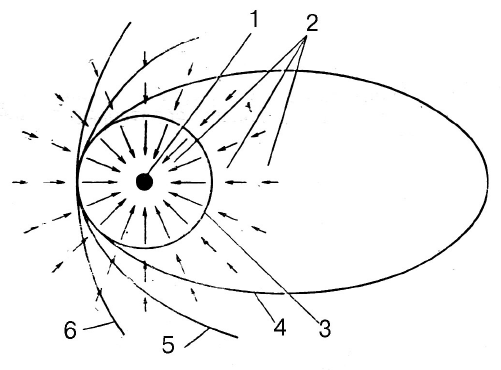
Рис. 2.2. Орбиты космического аппарата в поле центрального тела

1 – центральное тело; 2 – силовое поле центрального тела; 3 – круговая орбита; 4 – эллиптическая орбита; 5 – параболическая орбита; 6 – гиперболическая орбита

Рис. 2.3. Элементы орбиты ИСЗ

i – наклонение орбиты: а – большая полуось орбиты; W – долгота восходящего угла; w – угловое расстояние перигея от восходящего узла;

1 – направление на точку весен­него равноденствия; 2 – центр орбиты; 3 – линия узлов; 4 – нисходящий узел; 5 – Зем­ля; 6 – перигей орбиты (точка орбиты, ближайшая к центру Земли); 7 – плоскость ор­биты; 8 – плоскость экватора Земли; 9 – восходящий узел; 10 – фокус орбиты; 11 – апогей орбиты (точка орбиты, наиболее удаленная от центра Земли)

2.2. Силы и моменты, действующие на ла на активном участке траектории полета

ЛА, совершающий полет на активном участке траектории, рассматривают как точку переменной массы. Классическая механика, при установлении соотношений между силами, действующими на материальную точку и ее ускорением, исходит из постоянства массы точки, поэтому ее законы для изучения движения точек переменной массы неприменимы.

Задачу вывода зависимостей, учитывающих изменение массы в процессе движения, впервые решил И.В. Мещерский, разработавший общую теорию движения точки переменной массы.

2.2.1. Движение точки переменной массы

В классической механике для решения задач поступательного движения тела массой M = const используют уравнение:

(2.1)

– сумма проекций всех внешних сил на направление движения.

Как изменится это выражение в случае M = var?

Рассмотрим ракету, имеющую в момент t массу М, абсолютную скорость V, летящую в безвоздушном пространстве при отсутствии гравитационного поля. С борта ракеты за время t отбрасывается масса М с относительной скоростью W = V – V₁ противоположно направлению . Тогда абсолютная скорость массы М будет V₁ = V – W, а абсолютная скорость массы М – М соответственно – V – V (V – приращение скорости в результате отброса массы М).

По закону сохранения количества движения:

MV = (M – M)(V + V) + M(V – W). (2.2)

Пренебрегая величинами второго порядка малости, получим:

MV = M W . (2.3)

Из (2.3) следует, что в процессе i-го отброса массы M_i ракета приобретает приращение скорости:

. (2.4)

При последовательном отбросе ряда элементарных масс M_i ракета непрерывно будет получать приращение скорости V_i, а ее скорость в любой момент времени  , предшествующий очередному i-му отбросу массы M_i будет:

. (2.5)

Откуда после i-го отброса массы скорость ЛА:

V_i = V_i-1 + V_i .

Поделив левую и правую части (2.3) на t и перейдя к пределу при t  0, получим уравнение движения точки переменной массы (уравнение Мещерского):

. (2.6)

Обозначим секундный расход массы (но не веса!):

, [кг/с] .

Часто вместо массового, рассматривают секундный весовой расход:

, [кг/с] .

Тогда уравнение Мещерского:

, (2.7)

или:

В правой части выражения (2.7) – реактивная сила, обусловленная отбросом элементарных активных масс. Это основная движущая сила, но это еще не тяга двигателя (!)

Применительно к движению ракеты в среде без действия внешних сил реактивная сила будет единственной, действующей на ракету. Эта сила является движущей, если , т.е. в процессе движения масса уменьшается.

Из выражения (2.4) следует, что по мере движения ракеты непрерывно растет ее ускорение.

Из выражения (2.5) следует, что конечная скорость ракеты определяется величиной ее активной массы – запасом топлива, увеличение которого на борту приводит к увеличению ее скорости.