
Сложная или (m, p)-рента
Простая рента предполагала одно начисление или один учет на одном периоде ренты и одну выплату на этом периоде. Пусть теперь на одном периоде производится m начислений или учетов процентов и p выплат. Найдем коэффициенты сложной ренты и, соответственно, современную и наращенную денежные стоимости.
Найдем коэффициенты дисконтирования и наращения сложной ренты пренумерандо и постнумерандо. Напомним, что
v=1–d
– годовой коэффициент дисконтирования по годовой эффективной учетной ставке,
k=1+i
- годовой коэффициент наращения по годовой эффективной процентной ставке,
vm
=
![]()
- годовой коэффициент дисконтирования по годовой номинальной учетной ставке с m учетами в году,
km
=
![]()
- годовой коэффициент наращения по годовой номинальной процентной ставке,
vm,p
=
![]()
- годовой коэффициент
дисконтирования по годовой номинальной
учетной ставке с m
учетами на
![]() части года,
части года,
km,p
=
![]()
- годовой коэффициент наращения по годовой номинальной процентной ставке с m начислениями на части года.
На каждом частичном
периоде выплата равна
![]() .
Однако, величину
в этой выплате обычно учитывают в
коэффициентах ренты. Тогда
.
Однако, величину
в этой выплате обычно учитывают в
коэффициентах ренты. Тогда
![]() =
(1
+
+
=
(1
+
+
![]() + … +
+ … +
![]() )
= =
∙
)
= =
∙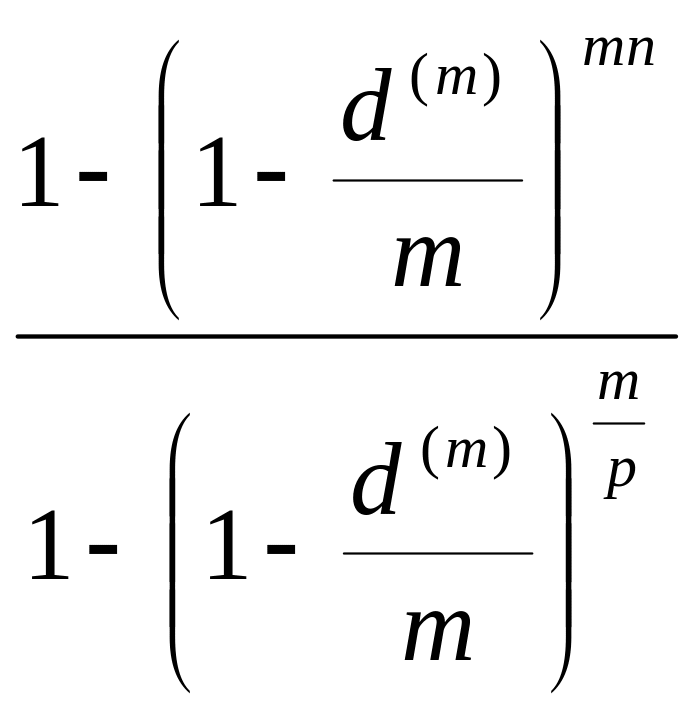
Очевидно, что коэффициент дисконтирования сложной ренты постнумерандо меньше коэффициента сложной ренты пренумерандо. Точнее, он равен
![]() vm,p
vm,p
или
![]() =
∙
=
∙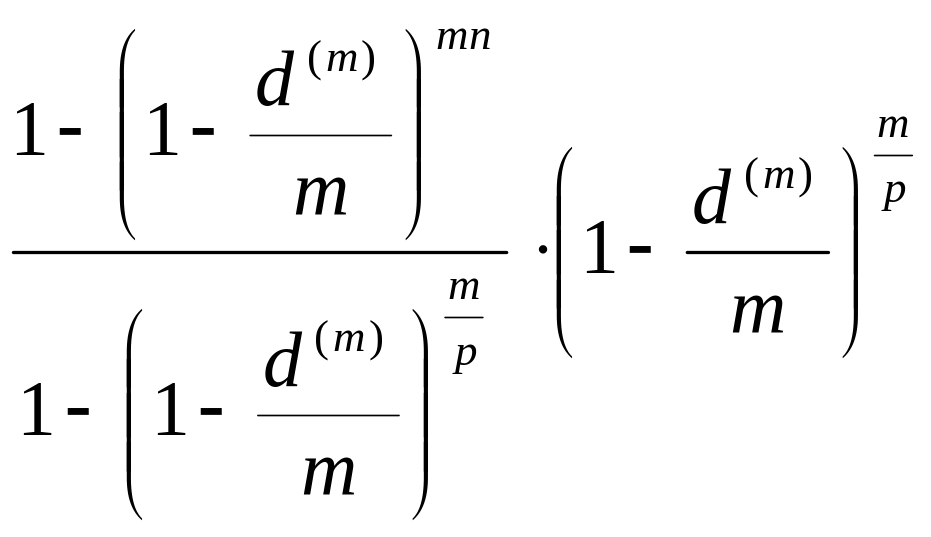
По аналогии коэффициент наращения сложной ренты пренумерандо равен:
![]() =
(
=
(![]() +
+
![]() + … +
+ … +
![]() )
=
)
=
=
∙
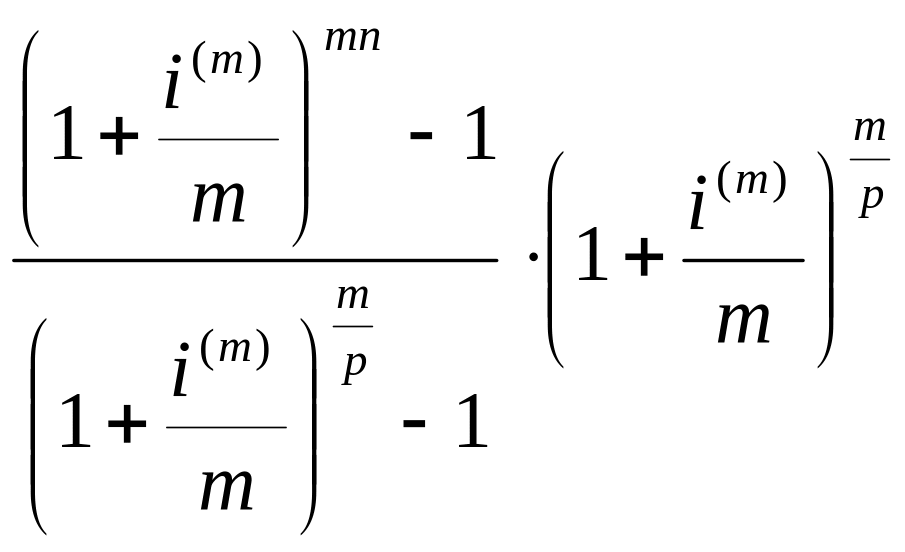 .
.
Коэффициент наращения сложной ренты постнумерандо равен:
![]()
или
![]() =
∙
=
∙
Итак, основные расчетные формулы для коэффициентов дисконтирования и наращения сложной ренты пренумерандо и постнумерндо имеют следующий вид:
= ∙ (3.13)
= ∙ (3.14)
= ∙ (3.15)
∙ = (3.16)
С помощью формул (3.13) – (3.16) легко записать основные расчетные формулы для современных и наращенных стоимостей сложной ренты-пренумерандо и постнумерндо:
S0 (0) = R (3.17)
S0 (n) = R (3.18)
S1 (0) =R (3.19)
S1 (n) = R (3.20)
Рассмотрим несколько типичных случаев сложной ренты:
m = 1, p = 1 – простая рента, (d(1) = d)
=
![]() =
=
(см. формулу (3.5))
Аналогично, коэффициенты (3.14), (3.15), (3.16) в этом случае равны коэффициентам (3.6), (3.7), (3.8) простой ренты.
m < ∞, p = 1
Формулы (3.13) – (3.16) примут следующий вид:
![]() =
=
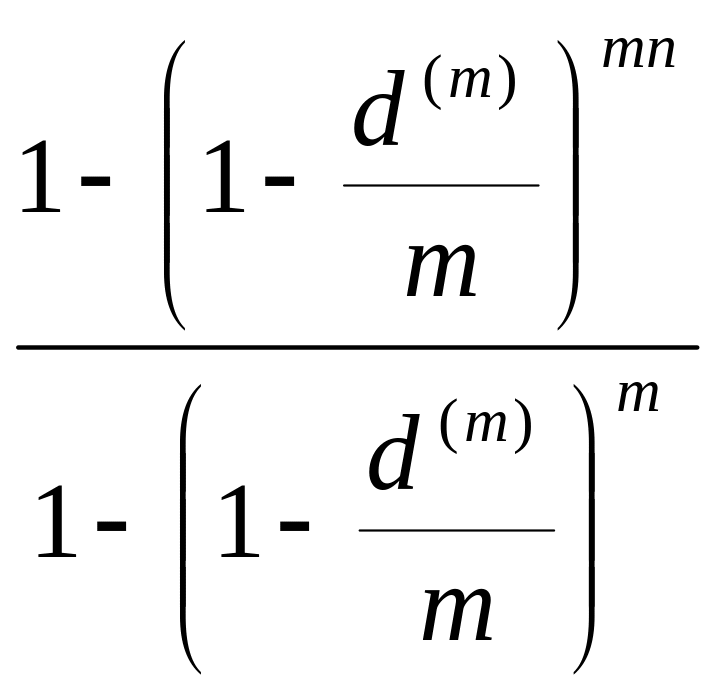 (3.21)
(3.21)
![]() =
=
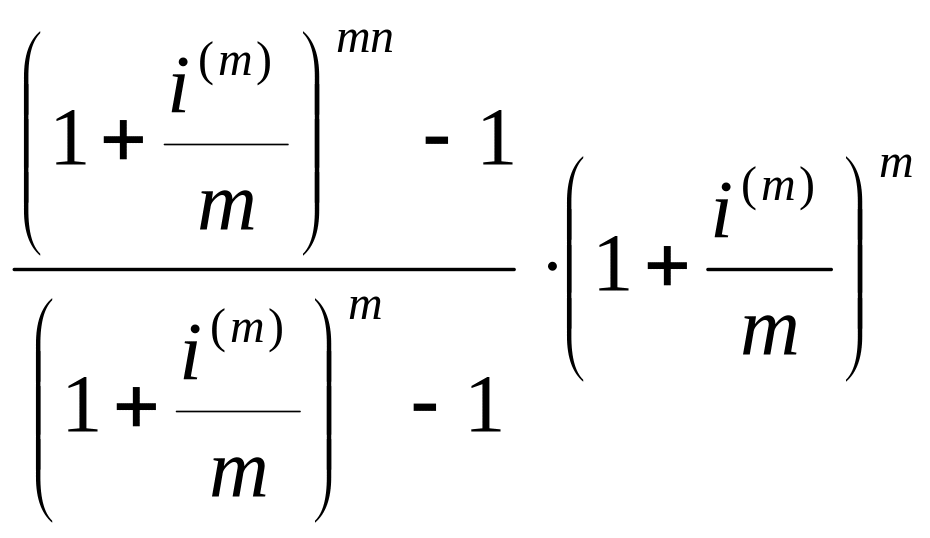 (3.22)
(3.22)
![]() =
=
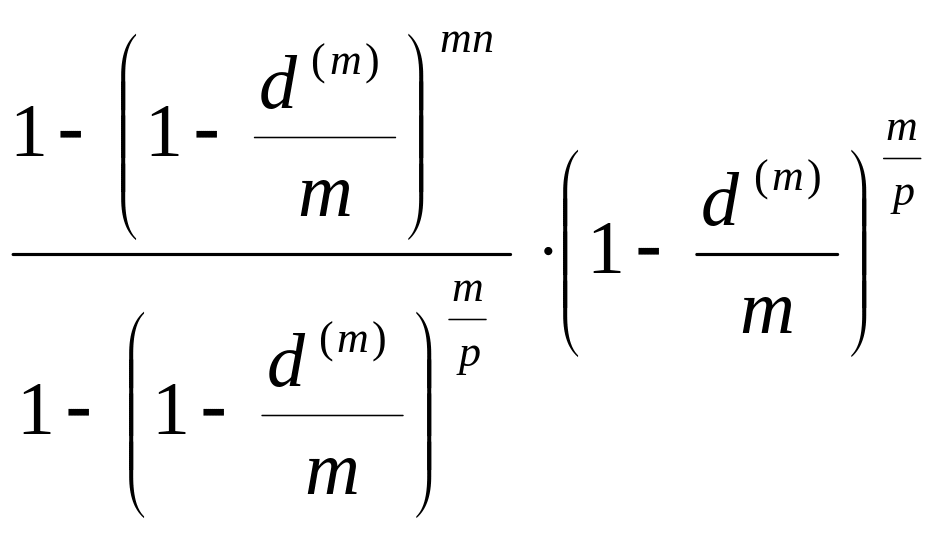 (3.23)
(3.23)
![]() =
=
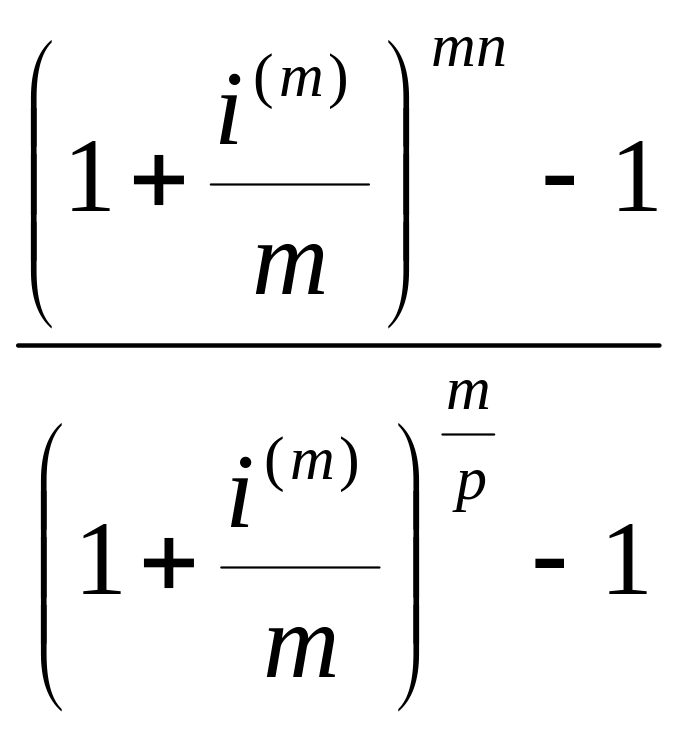 (3.24)
(3.24)
m = 1, p < ∞ (i(1) = i; d(1) = d)
![]() =
=
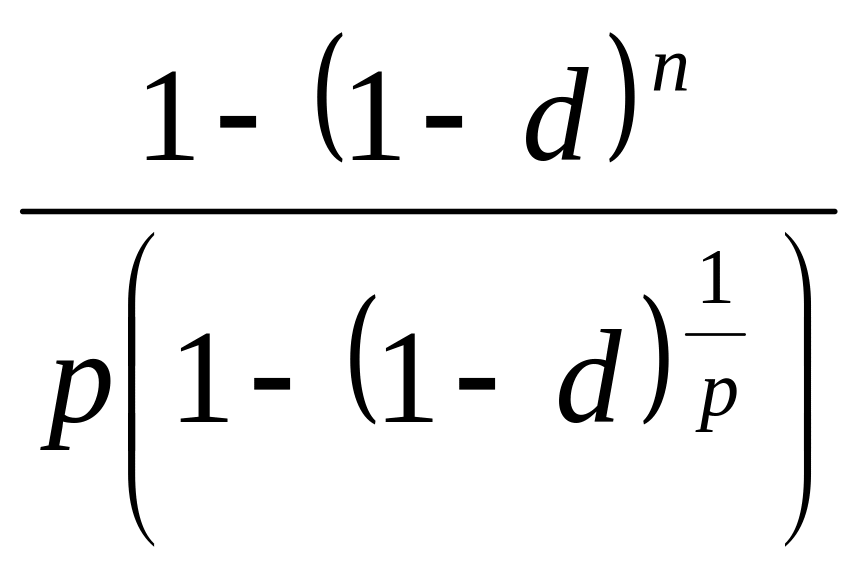 (3.25)
(3.25)
![]() =
=
 (3.26)
(3.26)
![]() =
=
 (3.27)
(3.27)
![]() =
=
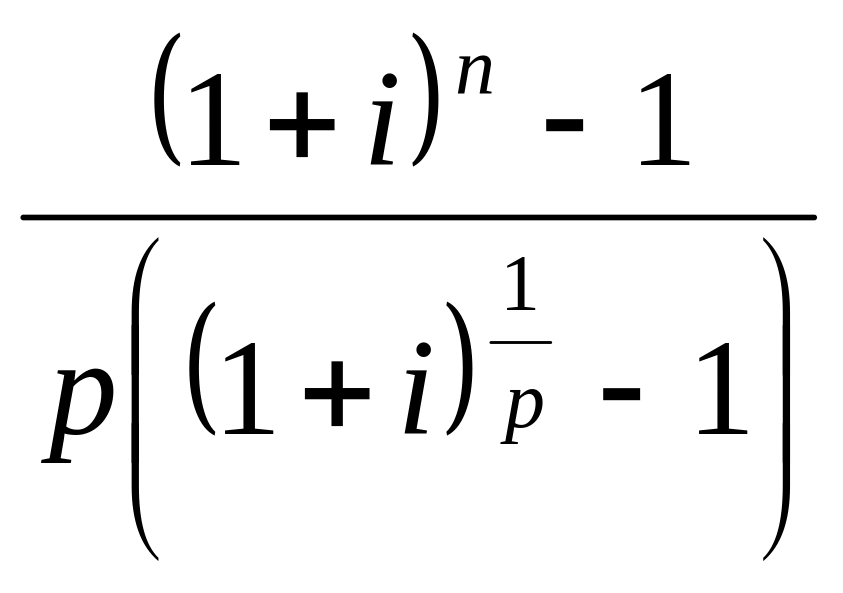 (3.28)
(3.28)
m = p
![]() =
=
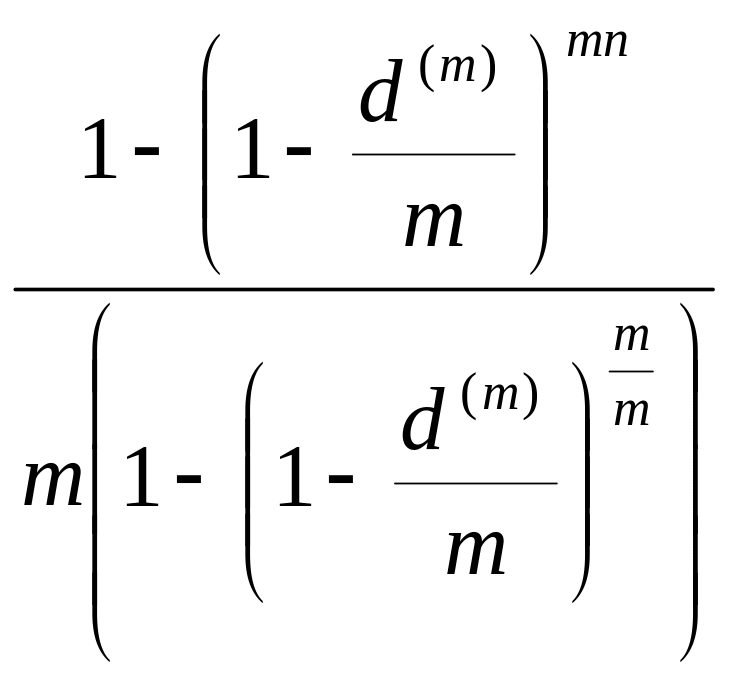 =
=
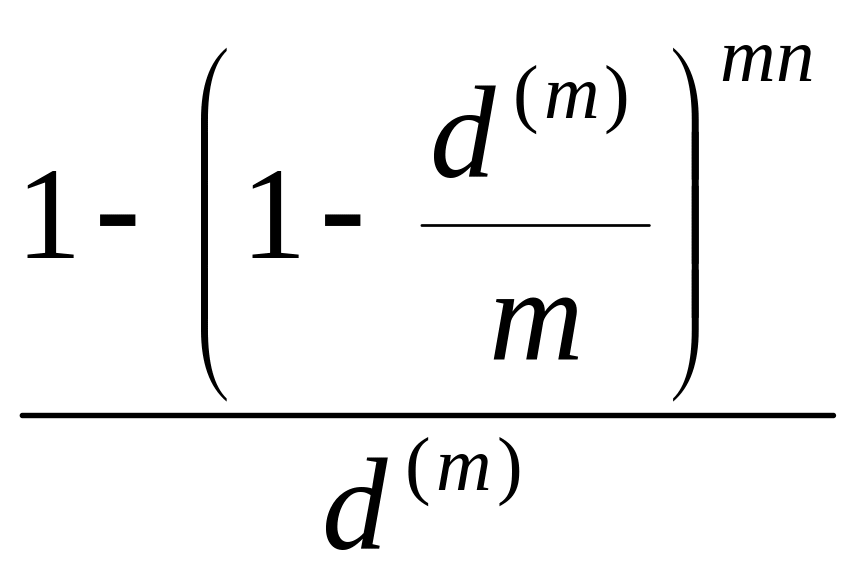 (3.29)
(3.29)
![]() =
=
 (3.30)
(3.30)
![]() =
=
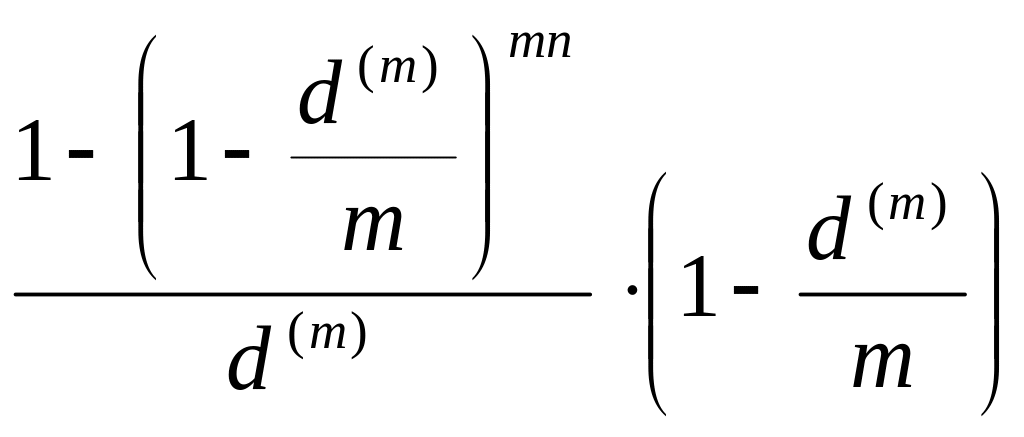 (3.31)
(3.31)
![]() =
=
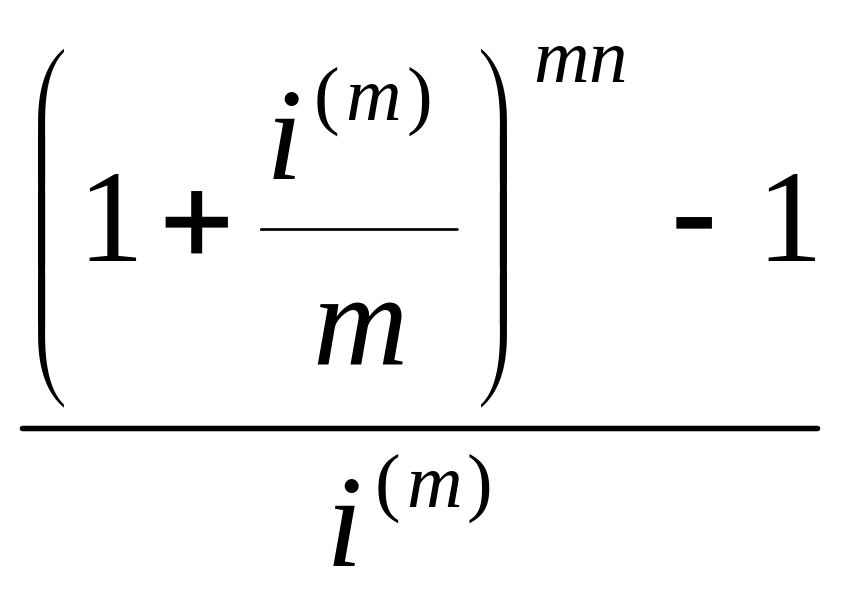 (3.32)
(3.32)
Итак, в случае m = p сложная рента с основным временным промежутком в один год сводится к простой ренте с основным временным промежутком, равным 1/m части года и соответствующей ставкой.
m = ∞, p < ∞
Рассмотрим коэффициент
=
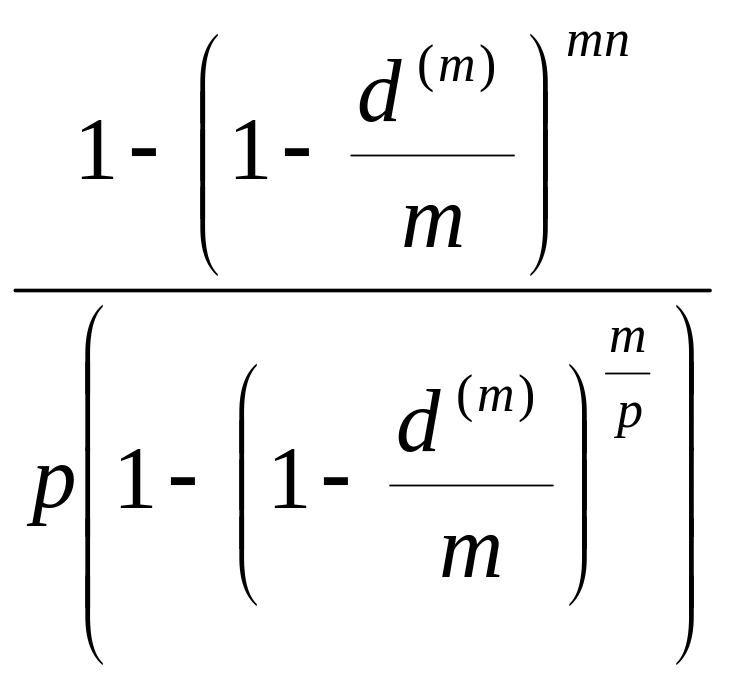
по формуле (3.13) и перейдем к пределу при m →∞. С помощью известного из высшей математики второго замечательного предела
![]()
легко получаем
![]()
Таким образом, коэффициент дисконтирования сложной ренты пренумерандо при непрерывном учете процентов по силе процента δ за n лет и p выплатах в году равен
![]() =
=
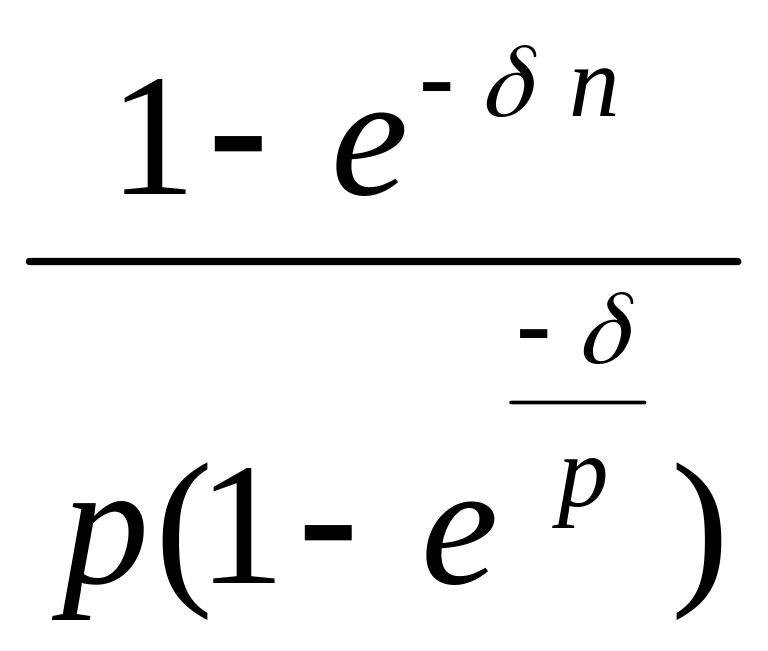 (3.33)
(3.33)
По аналогии получаем:
![]() =
=
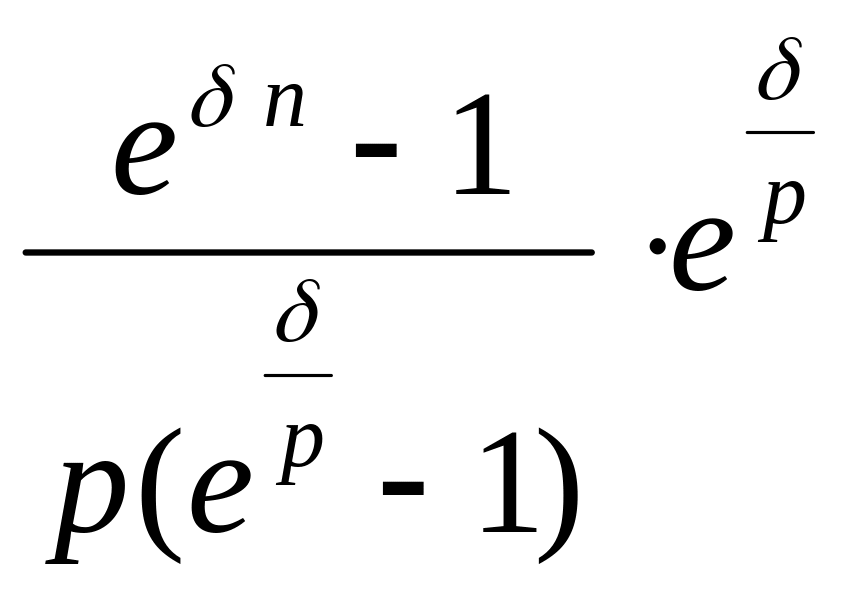 (3.34)
(3.34)
![]() =
=
 (3.35)
(3.35)
![]() =
=
 (3.36)
(3.36)
