3. Финансовая рента

Финансовая рента (аннуитет) – это поток платежей такой, что равные выплаты производятся через равные промежутки времени. Ренты бывают безусловные и условные. Рента называется безусловной, если известен общий срок ренты. Рента называется условной, если общий срок ренты заранее неизвестен и зависит от выполнения некоторого условия (например, страховые и пенсионные выплаты). Условные ренты обычно рассматриваются в актуарной математике. Различают также ренты пренумерандо и постнумерандо. Рента называется пренумерандо, если периодические выплаты производятся в начале каждого периода, постумерандо – если в конце каждого периода. Рента называется вечной, если ее общий срок неограниченно большой.

Введем обозначения:

Т – общий срок ренты

n – количество периодов ренты

τ – длительность одного периода

R – член ренты или периодическая выплата

Основными расчетными характеристиками ренты являются:

S₀ (0) – современная стоимость ренты пренумерандо

S₀ (n) – наращенная стоимость ренты пренумерандо

S₁ (0) – современная стоимость ренты постнумерандо

S₁ (n) – наращенная стоимость ренты постнумерандо

Ниже дано графическое изображение ренты пренумерандо и постнумерандо:

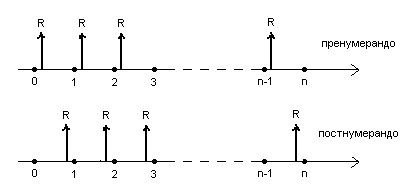
Рис. 1

Будем считать сначала, что рента простая, т.е. начисление или учет процентов, а также выплаты производятся один раз в году. Будем считать далее, что на рынке действуют следующие эквивалентные между собой ставки:

i ~ δ ~ d.

Вычислим величину S₀ (0). Используя формулу суммы геометрической прогрессии, а также равенство 1-v=d, получаем

S₀ (0) = R + Rv + Rv² + … + Rv^n–1 = R (1 + v + v² + … + v^n–1) =

Далее вычислим величину S₀ (n):

S₀ (n) = Rkⁿ + Rk^n–1 + Rk^n–2 + … + Rk = Rk (k^n–1 + k^n–2 + … + 1) =

Аналогично находим величины S₁ (0) и S₁ (n) относительно ренты постнумерандо. Окончательно получаем следующие расчетные формулы для простых рент пренумерандо и постнумерандо:

S₀ (0) = (3.1)

S₀ (n) = (3.2)

S₁ (0) = (3.3)

S₁ (n) = (3.4)

Финансовая рента часто используется в задачах погашения кредита.

Пример. Кредит в размере 300000 р. выплачивается ежегодно по годовой учетной ставке 20 % в течении 3-х лет. Найти величину ежегодных выплат.

Решение. Будем считать, что обслуживание кредита осуществляется по схеме простой ренты постнумерандо. Условие задачи: S₁ (0) = 300000, d = 20 %, n = 3. R = ?

Для нахождения члена ренты R воспользуемся формулой (3.3)

R =

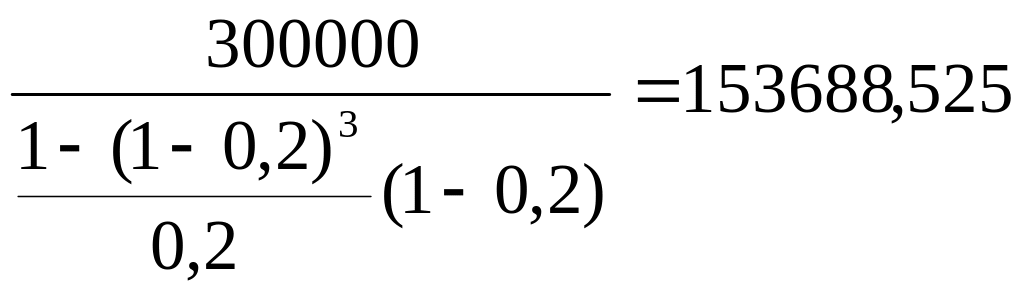
Ответ: R = 153688,53 р.

Нетрудно заметить, что справедливы неравенства:

S₀ (0) > S₁ (0)

S₀ (n) > S₁ (n)

Это означает, что современная или наращенная стоимость ренты пренумерандо больше соответствующей стоимости ренты постнумерандо. Безразмерные величины в формулах (3.1) – (3.4) – коэффициенты ренты.

Коэффициент дисконтирования ренты пренумерандо:

= (3.5)

Коэффициент наращения ренты пренумерандо:

(3.6)

Коэффициент дисконтирования ренты постнумерандо:

= (3.7)

Коэффициент наращения ренты постнумерандо:

= (3.8)

Формулы (3.5) – (3.8) подставим в формулы (3.1) – (3.4). Получаем выражения наращенных и дисконтированных стоимостей через коэффициенты наращения и дисконтирования рент пренумерандо и постнумерандо:

S₀ (0) = R (3.9)

S₀ (n) = R (3.10)

S₁ (0) = R (3.11)

S₁ (n) = R (3.12)