Аннуитеты

В большинстве современных коммерческих операций подразумеваются не разовые платежи, а последовательность денежных поступлений (или, наоборот, выплат) в течение определенного периода. Такая последовательность называется потоком платежей. Поток однонаправленных платежей с равными интервалами между последовательными платежами в течение определенного количества лет называется аннуитетом.

Аннуитет, для которого платежи осуществляются в начале соответствующих интервалов, носит название аннуитета пренумерандо; если же платежи осуществляются в конце интервалов, мы получаем аннуитет постнумерандо (обыкновенный аннуитет) – пожалуй, самый распространенный случай.

Введем следующие обозначения:

Р – величина каждого отдельного платежа;

i_с – сложная процентная ставка, по которой начисляются проценты;

S_k – наращенная сумма для k-го платежа аннуитета постнумерандо;

S – наращенная (будущая) сумма всего аннуитета постнумерандо (т. е. сумма всех платежей с процентами);

A_k – современная величина к-го платежа аннуитета постнумерандо;

А – современная величина всего аннуитета постнумерандо.

п – число платежей.

Аннуитет постнумерандо

Аннуитет постнумерандо с ежегодными платежами Р в течение n лет, на которые начисляются проценты по сложной годовой ставке i_c .

Общая наращенная сумма определяется по формуле:

где k_i,n – коэффициент наращения в удобном для вычислений виде равен:

Коэффициент наращения может быть определён по таблице 3 наращенного значения аннуитета.

Пример 9. Для погашения пакета облигаций, выпущенных ОАО «Интерком» на 5 лет, создаётся выкупной фонд. Ежегодные платежи предприятия в него составляют 150 000 руб., на них в конце каждого года начисляются проценты по ставке 7 %. Определите итоговую наращенную сумму денежных средств.

Решение. Для расчёта будущей стоимости выкупного фонда используем формулу

Коэффициент наращения определим по формуле Аналогичный результат получим по таблице.

Итоговая наращенная сумма будет равна S = P ∙ 150 000 ∙ 5,7507 = 862605 руб.

Таблица 3. Коэффициенты наращения аннуитета

Аннуитет пренумерандо

Аннуитет пренумерандо с ежегодными платежами Р в течение n лет, на которые начисляются проценты по сложной годовой ставке i_c .

Очевидно, отличие от предыдущего случая состоит здесь в том, что период начисления процентов на каждый платеж увеличивается на один год, т. е. каждая наращенная сумма S_k увеличивается в (1 + i_c) раз. Следовательно, для всей суммы S_n имеем S_n =S(1 + i_c).

Для коэффициента наращения аннуитета пренумерандо получаем следующее соотношение:

Для определения современных значений каждого платежа дисконтирование по заданной ставке i_c проводится на один раз меньше, чем в случае аннуитета постнумерандо. Поэтому каждая современная величина А_к будет больше в (1 + i) раз. Таким образом, А_п = А(1 + i_c). А для коэффициента приведения a _i,n^п получаем

Для определения коэффициентов наращения и приведения обыкновенного аннуитета существуют таблицы, которыми удобно пользоваться в практических вычислениях. Нужно иметь в виду, что n в данном случае – не число лет, а число периодов одинаковой продолжительности (день, месяц, квартал и т. д.), в которых принята данная процентная ставка. Таким образом, если задана годовая процентная ставка, можно найти эквивалентную ей ставку на более коротком интервале и рассматривать далее п как число таких интервалов.

Пример 10.

Найти современную величину потока платежей, определяемого следующим образом: первый год – поступления 500 руб., второй год – поступления 200 руб., третий год – выплата 400 руб., далее в течение семи лет – доход по 500 руб. Ставка дисконтирования – 6% годовых.

Решение.

В данном примере поток платежей в течение последних семи лет представляет собой постоянный аннуитет. По формуле 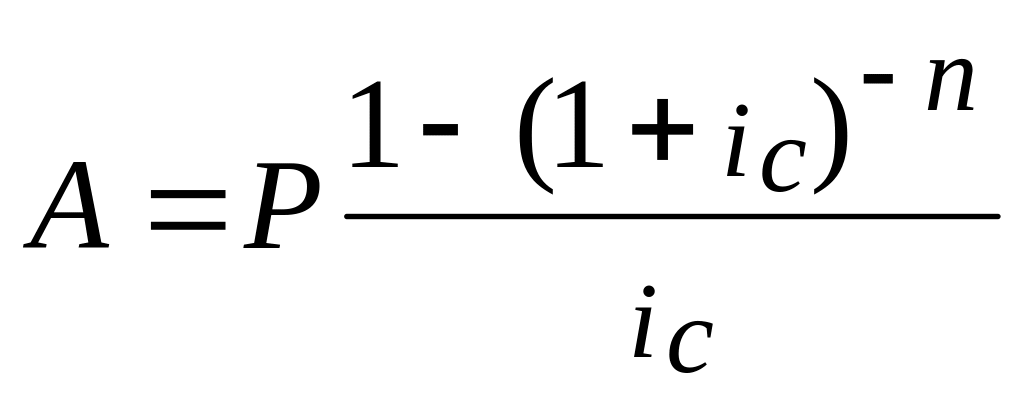мы можем рассчитать его современную величину A₀. Нельзя забывать, что это будет современная величина на момент начала четвертого периода: A₀ = 500 • 5,58 = 2791 руб. (коэффициенты приведения находим по таблице 4.

Далее, используя формулу , находим современные значения на момент начала потока платежа для всех оставшихся платежей и величины A₀:

А₁ = 500 • 0,943 = 471,5 руб.;

А₂ = 200 • 0,890 = 178,0 руб. ; А₃ = -400 • 0,840 = -336,0 руб.;

А₄ = 2791• 0,840 = 2344,4 руб.;

Складывая получившиеся величины, находим современную величину всего потока платежей: А₀ = А₁ + А₂ + А₃ + А_А = 2657,9 руб.

Таблица 4. Коэффициенты приведения аннуитета

_________________________________________________________________________________________