6. Способи виміру впливу факторів у стохастичному аналізі.

В економічному аналізі для вивчення впливу факторів на результативний показник широко використовується стохастичний факторний аналіз. Основними прийомами і способами даного аналізу є: кореляційний аналіз, дисперсійний аналіз, компонентний аналіз, дискримінантний аналіз тощо. Найбільш широко в економічних дослідженнях застосовується прийоми кореляційного аналізу, які дозволяють кількісно виразити взаємозв’язок між показниками.

6.1. Кореляційний аналіз.

Кореляційний аналіз застосовується для виміру впливу факторів, коли взаємозв’язок показників неповний, імовірнісний.

Кореляційний (стохастичний) зв’язок – це неповна вірогідна залежність між показниками, що виявляється тільки в значній кількості спостережень.

Розрізняють парну і множинну кореляції. Парна кореляція – це зв’язок між двома показниками, один з яких є факторним, а другий – результативним. Множинна кореляція виникає від взаємодії кількох факторів і результативного показника.

Необхідні умови застосування кореляційного аналізу такі:

• наявність достатньо великого числа спостережень за величиною досліджуваних факторів і результативних показників (у динаміці або за поточний рік за сукупністю однорідних об’єктів);

• досліджувані фактори належить вимірювати кількісно і відображати в тих чи інших джерелах інформації.

Застосування кореляційного аналізу дає змогу вирішити такі завдання:

• визначити зміну результативного показника під впливом одного або кількох факторів (в абсолютному вимірі), тобто дізнатися, на скільки одиниць змінюється величина результативного показника при зміні факторного на одну одиницю;

• встановити відносний ступінь залежності результативного показника від кожного фактора.

Кореляційний аналіз складається з кількох етапів.

На першому етапі визначають фактори, які справляють вплив на результативний показник, і відбирають найсуттєвіші для кореляційного аналізу. Від того, наскільки правильно зроблено відбір факторів, залежить точність висновків аналізу. При цьому необхідно дотримувати таких правил:

• фактори мають перебувати в причинно-наслідковому зв’язку з результативним показником;

• необхідно відбирати найбільш значущі фактори, які справляють відчутний вплив на результативний показник;

• фактори мають бути вимірними кількісно, тобто мати одиницю виміру, а інформація про них має міститися в обліку або звітності;

• у кореляційну модель лінійного типу не рекомендують включати фактори, зв’язок яких з результативним показником має нелінійний характер;

• не рекомендують включати в кореляційну модель взаємопов’язані фактори (якщо парний коефіцієнт кореляції двох факторів більший від 0,85, то, за правилами кореляційного аналізу, один із них необхідно виключити, інакше це призведе до викривлення результатів аналізу);

• не бажано включати в кореляційну модель фактори, зв’язок яких із результативним показником має функціональний характер.

Велику допомогу у відборі факторів для кореляційної моделі надають аналітичні угруповання, спосіб порівняння паралельних і динамічних рядів, лінійні графіки. За їхньою допомогою можна визначити наявність, напрям і форму залежності показників, що вивчаються. Відбір факторів можна також проводити в процесі вирішення завдань кореляційного аналізу на основі значущості їх за критерієм Стьюдента.

На другому етапі збирають вихідну інформацію про кожний факторний і результативний показник. Її можна перевірити на точність, однорідність і відповідність закону нормального розподілу.

Передовсім необхідно переконатися у достовірності інформації, наскільки вона відповідає об’єктивній дійсності. Використання недостовірної, неточної інформації призводить до неправильних результатів.

Одна з умов кореляційного аналізу – однорідність досліджуваної інформації відносно розподілу її близько до середнього рівня. Якщо в сукупності є групи об’єктів, які значно відрізняються від середнього рівня, то це вказує на неоднорідність початкової інформації. Критеріями однорідності інформації слугують середньоквадратичне відхилення і коефіцієнт варіації, які розраховують за кожним факторним і результативним показником.

Середньоквадратичне відхилення показує абсолютне відхилення значень від середньоарифметичного. Його визначають за формулою:

.

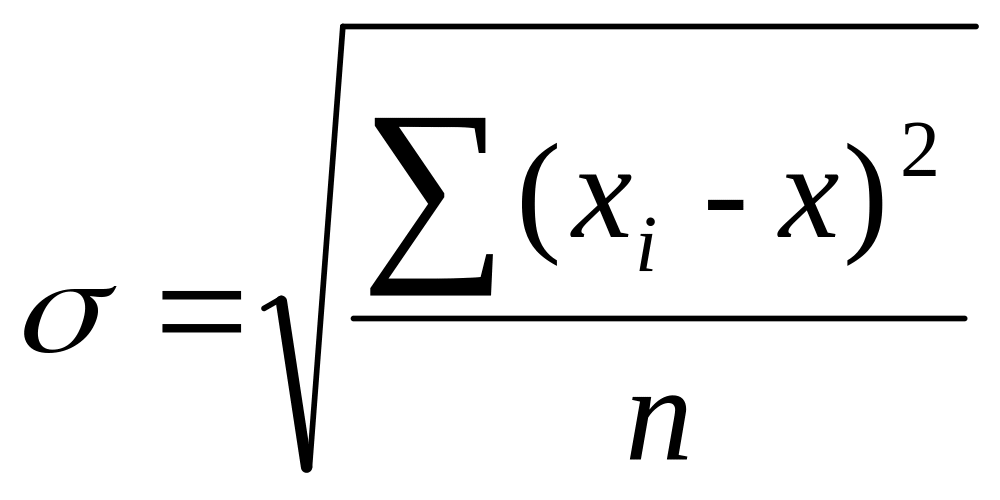Коефіцієнт варіації показує відносний ступінь відхилення окремих значень від середньоарифметичного. Його розраховують за формулою:

.

Чим більший коефіцієнт варіації, тим відносно більший розкид і менша вирівнюваність об’єктів, що вивчаються. Змінюваність варіаційного ряду вважають незначною, якщо варіація не перевищує 10 %, середньою – якщо становить 10-12 %, значною – коли вона більша ніж 20 %, але не перевищує 33 %. Якщо варіація вища ніж 33 %, то це вказує на неоднорідність інформації і необхідність виключення нетипових спостережень, які звичайно бувають у перших і останніх ранжованих рядах вибірки.

Наступні вимоги до вихідної інформації – підпорядкування її закону нормального розподілу. Для кількісного оцінювання ступеня відхилення інформації від нормального розподілу слугують відношення показника асиметрії до її помилки і відношення показника ексцесу до його помилки.

Показник асиметрії (А) і його помилку (m_a) розраховують таким чином:

.

Показник ексцесу (Е) і його помилку (m_e) розраховують у такий спосіб:

.

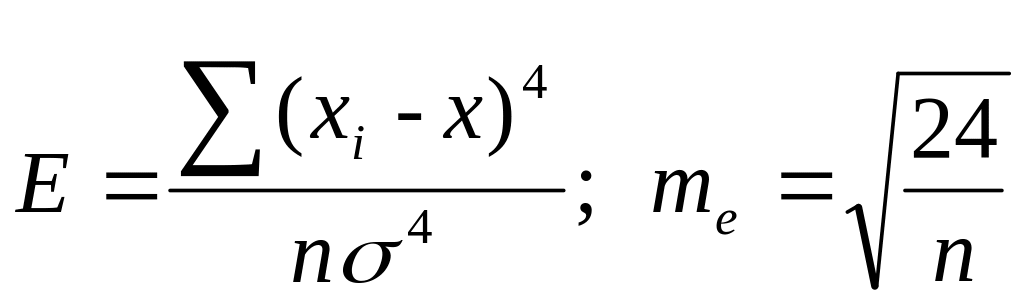У симетричному розподілі А = 0. Відмінність від нуля вказує на наявність асиметрії в розподілі даних близько середньої величини. Від’ємна асиметрія свідчить про те, що переважають дані з великими значеннями, а з меншими значеннями трапляються значно рідше. Додатна асиметрія показує, що частіше трапляються дані з невеликими значеннями.

У нормальному розподілі показник ексцесу Е = 0. Якщо Е > 0, то дані густо згруповано близько середньої і вони утворюють гостровершинність. Якщо Е < 0, то крива розподілу буде плосковершинною.

Коли відношення А / m_a і Е / m_e менше від 3, то асиметрія й ексцес не мають суттєвого значення, і досліджувана інформація є відповідною до закону нормального розподілу. Отже, її можна використати для аналізу.

На третьому етапі моделюють зв’язок між факторами і результативним показником, тобто вибирають і обґрунтовують математичне рівняння, яке найточніше виражає суть досліджуваної залежності.

Залежність результативного показника від його визначальних факторів можна виразити рівнянням парної і множинної регресії. При прямолінійній формі вони мають такий вигляд:

• рівняння парної регресії: y = a + bx;

• рівняння множинної регресії: y = a + b₁x₁ + b₂x₂ + … + b_nx_n, де а – вільний член рівняння при х = 0; x₁, x₂, …, x_n – фактори, які визначають рівень результативного показника, що вивчається; b₁, b₂, ..., b_n – коефіцієнти регресії при факторних показниках, які характеризують рівень впливу кожного фактора на результативний показник в абсолютному вираженні.

Якщо зв’язок між результативним і факторними показниками має нелінійний характер, то можна використати ступеневу, логарифмічну, параболічну, гіперболічну та інші функції.

У тому разі, коли трудно обґрунтувати форму залежності, розв’язати задачу можна за різними моделями і порівняти отримані результати. Адекватність різних моделей фактичним залежностям перевіряють за критерієм Фішера, за показником середньої помилки апроксимації і величиною множинного коефіцієнта детермінації.

На четвертому етапі роблять розрахунок основних показників зв’язку кореляційного аналізу: рівняння зв’язку, коефіцієнти кореляції, детермінації, еластичності та ін.

Наприклад, розрахунок рівняння зв’язку (y = a + bx) зводиться до визначення параметрів а і b за допомогою методу найменших квадратів, який дає такі значення параметрів:

, .

Якщо значення а і b підставити у рівняння прямої лінії y = a + bx, дістанемо шукану функцію (модель) залежності між у і х.

Для виміру щільності зв’язку між факторними і результативними показниками обчислюють коефіцієнт кореляції.

У разі прямолінійної форми зв’язку між показниками, що вивчаються, коефіцієнт кореляції розраховують за такою формулою:

.

Коефіцієнт кореляції може набирати значень від 0 до 1. Чим ближча його величина до 1, тим тісніший зв’язок між показниками, і навпаки.

Якщо коефіцієнт кореляції піднести у квадрат, одержимо коефіцієнт детермінації:

.

П’ятий етап – статистична оцінка і практичне використання результатів кореляційного аналізу.

Щоб переконатися в надійності показників зв’язку і правомірності використання їх з практичною метою, необхідно дати їм статистичну оцінку. Для цього використовують критерій Стьюдента (t), критерій Фішера (F-відношення), середню помилку апроксимації (ε), коефіцієнти множинної кореляції (R) і детермінації (D).

Отже, кореляційний аналіз можна використовувати в економічному аналізі господарської діяльності підприємства: для розрахунку впливу факторів на зміну результативного показника; для підрахунку резервів підвищення рівня досліджуваного показника; для планування і прогнозування його величини. Крім того, багатофакторний кореляційний аналіз має важливе наукове і практичне значення. Це проявляється в тому, що значно поглиблюється факторний аналіз, унаслідок чого встановлюють місце і роль кожного фактора у формуванні рівня досліджуваних показників і, як результат, – точніше обґрунтовують плани та управлінські рішення, об’єктивніше оцінюють підсумки діяльності підприємств і повніше визначають внутрігосподарські резерви.