Основы проектирования машин / ГЛАВА 7.1

ГЛАВА 7.1.1 ГЕОМЕТРИЯ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ ПЕРЕДАЧ

Профиль зуба колеса и его свойства. Рассмотрим профиль зуба колеса цилиндрической передачи с эвольвентным зацеплением. Как известно, эвольвента (или инволюта) окружности представляет собой кривую, центры кривизны которой принадлежат рассматриваемой окружности. Эвольвента окружности может быть

получена как траектория точки прямой, перекатывающейся без скольжения по этой окружности радиусом rb , называемой основной окружностью (рис. 7.1.1). В дальнейшем для краткости эвольвенту окружности будем

называть просто эвольвентой E .

Выражение tgα −α называется инволютой угла профиля α и обозначается как invα . Инволюта

На рис. 7.1.2 изображен контакт двух эвольвент окружностей, проведенных радиусами rb1 и rb2 из

центров O1 и O2 . При вращении звеньев 1 и 2 точка касания эвольвент перемещается вдоль отрезка AB , так как направления нормалей к поверхностям эвольвент первого и второго звеньев должны совпадать и быть

касательными к основным окружностям. Следовательно, для колес с эвольвентным зацеплением линия зацепления (геометрическое место точек контакта профилей зубьев при вращении) представляет собой прямую. Если к тому же учесть, что эвольвента - единственная известная в математике кривая, обеспечивающая прямую линию зацепления, то становится понятным широкое распространение зацепления этого типа.

Рис. 7.1.2

Точка пересечения общей нормали к эвольвентам с межосевой линией называется полюсом зацепления

P . Окружности радиусами O1 P и O2 P называются начальными окружностями. В дальнейшем все величины, относящиеся к начальной окружности, будем снабжать индексом W . Радиусы начальных окружностей колес

обозначим через rW1 и rW 2 , а радиусы основных окружностей - как rb1 и rb2 . Положение нормали к

поверхности определяется углом αW (т.е. углом между линией зацепления и нормалью к линии центров), который называется углом зацепления.

Эвольвентное зацепление характеризуется постоянным передаточным отношением u . Покажем это. Очевидно, что линейная скорость в контакте постоянна, направлена вдоль линии зацепления и может быть

определена через параметры либо первого, либо второго звеньев:

Постоянство передаточного отношения объясняется тем, что при передаче постоянного момента нормальная сила в контакте двух эвольвент неизменна по величине и направлена вдоль линии зацепления.

Нарезание зубьев колес зубчатых передач. Одним из наиболее сложных технологических процессов при изготовлении зубчатых колес является их нарезание и последующая механическая обработка. Для нарезания используются специальные станки и инструменты, с помощью которых реализуются методы копирования или обкатки. При первом способе зуб принимает форму, очерченную инструментом, а во втором случае имитируется процесс зацепления колес, одно из которых выполняет роль инструмента.

Остановимся более подробно на втором способе (рис. 7.1.3). В качестве инструмента будем рассматривать рейку 1, которая представляет собой инструментальное колесо бесконечного радиуса начальной окружности. При таком способе наpезания заготовка колеса 2 вращается относительно оси, а рейка для обеспечения резания перемещается в двух направлениях: по касательной к окружности заготовки и вдоль оси). След от рейки является эвольвентой, параметры которой зависят от вида профиля рейки. Полученный нарезанием рейкой зуб зубчатого колеса показан на рис. 7.1.4.

Рис. 7.1.5

Наиболее часто используется профиль, изображенный на pис. 7.1.5, со следующими параметрами: угол профиля α ; коэффициент высоты головки зуба ha* = ha / m ( ha - высота головки); коэффициент высоты ножки

Приведем несколько примеров стандартных параметров профиля:

•цилиндрические колеса

α = 200 ; ha* =1; hl* =2 ; c* = 0,25 ; ρf = 0,38m .

•прямозубые конические колеса

Полученный после нарезания зубьев колеса окружной шаг не постоянен по высоте зуба. Окружность, для которой шаг рейки совпадает с шагом инструмента, называется делительной окружностью. Средняя линия контура называется делительной прямой. Расстояние между осями колес называется межосевым расстоянием и

обозначается как aW .

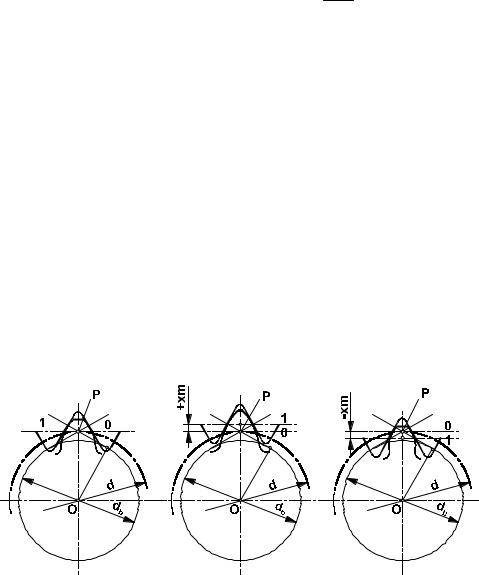
а) Передачи без смещения. Если делительная окружность колеса является касательной к средней линии контура инструмента, то имеет место нарезание без смещения. В этом случае начальные окружности колес совпадают с делительными. На рис. 7.1.6a показан вариант зацепления колес, нарезанных без смещения. Здесь диаметры делительных окружностей касаются в точке полюса, а угол зацепления равен углу профиля зуба рейки.

Рис. 7.1.6

Очевидно, что при нарезании без смещения диаметр d1 делительной окружности колеса с числом зубьев z1 равен

Подставляя (7.1.9) и (7.1.17) в (7.1.15), запишем еще одно полезное соотношение

a = 0,5d2 u u+1 ,

откуда следует

Выражение для определения делительного диаметра колеса в форме (7.1.18) понадобится нам в дальнейшем при расчетах на прочность.

б) Передачи со смещением. При нарезании со смещением (рис. 7.1.6 b,c) диаметр начальной окружности не касается средней линии контура инструментальной рейки. Смещение рейки позволяет избежать подреза ножки зуба при изготовлении колес с малым числом зубьев и повлиять на прочностные характеристики зубьев.

На рис. 7.1.7 приведено три варианта возможного размещения инструмента относительно центра колеса. Вариант а) соответствует рассмотренному выше случаю нарезания без смещения. Назовем это положение

начальным, и тогда начальная прямая 0 совпадет с делительной прямой 1. Вариант b) иллюстрирует случай

положительного смещения, когда делительная прямая лежит выше начальной прямой (здесь x - коэффициент смещения инструмента), а вариант c) соответствует отрицательному смещению. Если колеса нарезаны с

положительным смещением, то межосевое расстояние и угол контакта возрастают (рис. 7.1.6b).

В зависимости от положения рейки зуб колеса очерчивается разными участками эвольвенты, и форма зуба при этом меняется. На рис. 7.1.8 изображена качественная картина форм зубьев для различных вариантов смещения. Как видно из рисунка, при положительном смещении толщина зуба по дуге делительной окружности увеличивается, а при отрицательном - уменьшается. Изменение геометрических параметров влечет за собой изменение прочностных характеристик.

Рис. 7.1.7

Расчет геометрии передачи со смещением проведем на примере внешнего зацепления пары колес. Радиусы начальных окружностей можно определить с помощью выражений (7.1.7):

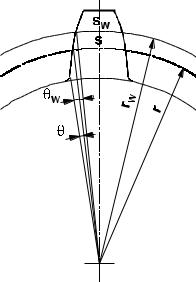
Для нахождения угла зацепления необходимо установить зависимость толщины зуба s на диаметре d от толщины sW на диаметре dW начальной окружности. Из геометрических соображений (рис. 7.1.9) видно, что

Рис. 7.1.9

Учитывая, что толщина зуба по делительной окружности равна величине впадины, запишем

При положительном смещении рейки толщина зуба по делительной окружности увеличивается (рис. 7.1.10; штриховой линией обозначен исходный контур без смещения, сплошной - со смещением) на величину

2 AB = 2mxtgα . Тогда

Рис. 7.1.10

С учетом (7.1.35) выражение (7.1.34) переписывается в виде

По полученной инволюте (7.1.36) из таблицы эвольвентных углов (табл. 7.1.1) можно определить угол

зацепления αW , а также с помощью (7.1.25) рассчитать величину межосевого расстояния aW .

Особенности геометрического расчета косозубых и шевронных колес. Колесо, зуб

которого наклонен под углом β к оси вращения, называется косозубым. Два косозубых колеса с противоположным направлением зубьев образуют шевронное колесо. Прочность косозубых и шевронных колес

выше, чем прямозубых, за счет увеличения осевой длины контакта, причем чем больше угол наклона зуба, тем колесо прочнее. С другой стороны, увеличение угла вызывает значительные дополнительные осевые нагрузки,

поэтому для косозубых колес рекомендуется угол наклона принимать равным β = (8 ÷15)0 . Для шевронных

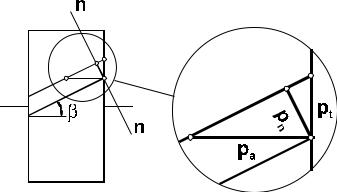
колес, в которых осевые нагрузки скомпенсированы противоположным направлением зубьев, диапазон для выбора угла наклона существенно расширяется: β = (30 ÷45)0 .

Рис. 7.1.11

Технологически изготовление косозубых колес не отличается от прямозубых. Разница только в том, что

инструмент при нарезании перемещается под углом β . Следовательно, параметры косозубого колеса в нормальном сечении совпадают с параметрами прямозубого. Модуль инструмента равен модулю в нормальном

сечении. В качестве расчетных параметров косозубых колес принимают параметры торцевого сечения. В

дальнейшем признаком нормального сечения будет наличие у соответствующих величин индекса n , а торцового

- t (рис. 7.1.11).

Модули торцевого и нормального сечений связаны соотношением

Подрезание профилей зубьев. Если количество зубьев колеса невелико, то может произойти явление, которое получило название подреза. В этом случае траектория относительного движения конца профиля зуба одного колеса пересекается с эвольвентной частью профиля зуба сопряженного колеса. Зуб, подрезанный у основания, теряет прочность. Подреза можно избежать, вводя смещение инструментального контура при нарезании. Без доказательства запишем

получаем zmin =17 .

Избежать подреза при нарезании малого числа зубьев можно также, меняя угол профиля. Для этого обычно применяется нестандартный профиль, выполненный с некоторым смещением. Минимальный коэффициент

смещения x , при котором нет подреза, можно определить из соотношения