8

Практическое занятие №2

Трансцендентные уравнения.

Методы решения трансцендентных корней

Ваша цель:

1. Научиться локализовать корни нелинейных уравнений;

2. Изучить итерационные методы уточнения корней с заданной точностью Ɛ.

Задача нахождения нелинейных корней уравнений вида , где F(x) – некоторая непрерывная функция, встречается в различных областях научных исследований. Нелинейные уравнения делятся на 2 класса:

• Алгебраические уравнения;

• Трансцендентные.

Алгебраическими уравнениями называются уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). Например, многочлен является целой алгебраической функцией.

Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.) называются трансцендентными.

Методы решения нелинейных уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторой формулы. Из школьного курса алгебры вам известны методы решения линейных, квадратных, показательных, тригонометрических уравнений.

Однако встречающиеся на практике уравнения не удаётся решить такими простыми методами. Для их решения используются итерационные методы, т.е. методы последовательных приближений. Алгоритм нахождения корня уравнения с помощью итерационного метода состоит из двух этапов:

1 этап – локализация корней, на котором находят достаточно узкие отрезки (или отрезок, если корень единственный), которые содержат один и только один корень уравнения . Часто вместо отрезка локализации достаточно указать начальное приближение к корню.

2 этап – итерационное уточнение корней, на котором вычисляют приближенное значение корня с заданной точностью.

Локализация корней

Отделить корни можно аналитически или графически. Если такие оценки исходного приближения провести не удаётся, то находят две близко расположенные точки a и b, в которых непрерывная ф-ия F(x) принимает значения разных знаков, т.е. F(a)* F(b)<0. В этом случае между точками a и b есть по крайней мере одна точка, в которой F(x)=0. В качестве начального приближения x₀ , можно принять середину отрезка [a;b] , т.е. x₀.= .

Пример 1

Отделить корни уравнения x⁴-x³-2x²+3x-3=0 аналитическим методом.

Полагая, что f(x)= x⁴-x³-2x²+3x-3, получаем производную f’(x)= 4x³-3x²-4x+3.

Найдем корни производной:

4x³-3x²-4x+3=0

4x(x²-1)-3(x²-1)=0

(4x-3)(x²-1)=0

x₁=1; x₂=-1; x₃=3/4 – точки перегиба функции.

Составим таблицу знаков функции:

x	-∞	-1	¾	1	+∞
F(x)	+	-	-	-	+

Из таблицы видно, что уравнение имеет два действительных корня: x₁€[-∞, -1], x₂€ [1,+ ∞].

Уменьшим промежутки, в которых находятся корни:

x	-2	-1	1	2
F(x)	+	-	-	+

Следовательно, x₁€[-2, -1], x₂€ [1, 2].

Пример 2

Отделить корни уравнения графическим методом.

Перепишем уравнение в виде . Построим графики функций: .

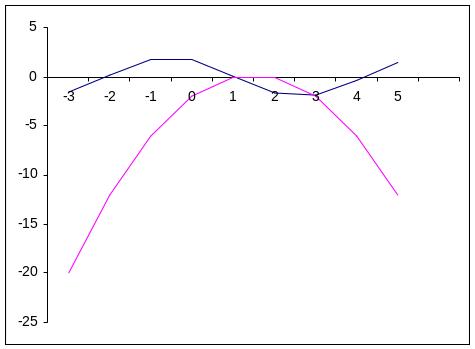
Из графика видно, что уравнение имеет два корня: x₁€[0,1; 1], x₂€ [2, 3].

Уточнение корней

Итерационный процесс уточнения корней состоит в последовательном уточнении начального приближения x₀. Каждый такой шаг называется итерацией. В результате итераций находится последовательность приближённых значений корня x₁, x₂, …, x_n. Если эти значения с ростом n приближаются к истинному значению корня, то говорят, что итерационный процесс сходится.

Метод дихотомии1

Пусть [a,b] – отрезок локализации. Предположим, что функция f(x) непрерывна на [a,b] и на концах принимает значения разных знаков . Возьмем произвольную точку с∈[a, b]. Вычисление f(c) приведет к какой-либо из трех ситуаций:

1. f(a)∙f(c)<0;

2. f(c)∙f(b)<0;

3. f(c) =0

Первые два случая ведут к сокращению промежутка [a,b], а третий случай маловероятен в смысле «прямого попадания», но реален в смысле приближенного значения f(c) ≈ 0.

Выбор точки с определяется разными способами, которые мы и рассмотрим.

Метод половинного деления

Алгоритм метода половинного деления состоит в построении последовательности вложенных отрезков, на концах которых функция принимает значения разных знаков. Каждый последующий отрезок получают делением пополам предыдущего.

Опишем один шаг итераций метода. Пусть на k-ом шаге найден отрезок такой, что . Найдем середину отрезка . Если , то - корень и задача решена. Если нет, то из двух половин отрезка выбираем ту, на концах которой функция имеет противоположные знаки:

, , если

 

, , если

 Критерий окончания итерационного процесса: Итерационный процесс продолжается до тех пор, пока значение функции F(x) после n-ой итерации не станет меньшим по модулю некоторого заданного малого числа , т.е. |F(c_n)|<.

Метод деления отрезка пополам довольно медленный, однако он всегда сходится, т.е. решение получается всегда и с заданной точностью, устойчив к ошибкам округления. Требуемое обычно большое число итераций не является препятствием, если каждое вычисление функции несложно.

Пример 3

Уточнить один из корней уравнения x⁴-x³-2x²+3x-3=0 методом половинного деления с точностью до сотых долей.

Уточним корень x₁€[-2, -1], используя следующую таблицу:

n	an+	bn-		xn4	-xn3	-2xn2	3xn	f(xn)
0	-2	-1	-1.5	5.0625	3.375	-4.5	-4.5	-3.5625
1	-2	-1.5	-1.75	9.3789	5.3594	-6.125	5.25	0.3633
2	-1.75	-1.5	-1.63	7.0591	4.3307	-5.3138	-4.89	-1.8140
3	-1.75	-1.63	-1.69	8.1573	4.8268	-5.7122	-5.07	-0.7981
4	-1.75	-1.69	-1.72	8.7521	5.0884	-5.9168	-5.16	-0.2363
5	-1.75	-1.72	-1.73	8.9575	5.1777	-5.9858	-5.19	-0.0406
6	-1.75	-1.73	-1.74	9.1664	5.2680	-6.0552	-5.22	0.1592
7	-1.74	-1.73

Ответ: x≈ -1.73

Метод хорд

В данном методе процесс итераций состоит в том, что в качестве приближений к корню уравнения F(x)=0 принимаются значения точек пересечения хорды с осью абсцисс с₀, с₁,….

Находим уравнение хорды АВ:

Уравнение прямой, заданное координатами двух точек:

Для точки пересечения её с осью абсцисс (x=c₀, y=0). Подставим. Получим уравнение:

Сравнивая знаки величин F(a) и F(c₀), выбираем тот отрезок, на концах которого функция принимает разные знаки.

, , если

 

, , если

Сравнивая знаки величин F(a) и F(c₀), выбираем тот отрезок, на концах которого функция принимает разные знаки. Итерационный процесс продолжается до тех пор, пока значение функции F(x) после n-ой итерации не станет меньшим по модулю некоторого заданного малого числа , т.е. |F(c_n)|<.

Эти алгоритмы похожи, но метод хорд в ряде случаев даёт более быструю сходимость итерационного процесса. При этом успех его применения гарантирован.