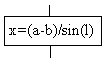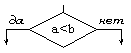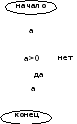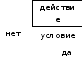Практикум_1_Алгоритмы
.docxПрактикум №1. Понятие алгоритма. Основные алгоритмические структуры
Цели:
-
Ознакомиться с понятием алгоритма и основными алгоритмическими структурами;
-
Научиться строить алгоритмы решения задачи;
-
Научиться описывать алгоритм с помощью блок-схемы.
АЛГОРИТМ – система правил, сформулированная на понятном исполнителю языке, которая определяет процесс перехода от допустимых исходных данных к некоторому результату и обладает свойствами массовости, конечности, определенности, детерминированности.
Слово «алгоритм» происходит от имени великого среднеазиатского ученого VIII–IXвв Аль-Хорезми (Хорезм – историческая область на территории современного Узбекистана). Термин алгоритм употреблялся для обозначения четырех арифметических операций, именно в таком значении он и вошел в некоторые европейские языки.
Слово «алгоритм» вновь стало употребительным с появлением электронных вычислительных машин для обозначения совокупности действий, составляющих некоторый процесс. Здесь подразумевается не только процесс решения некоторой математической задачи, но и кулинарный рецепт и инструкция по использованию стиральной машины, и многие другие последовательные правила, не имеющие отношения к математике, – все эти правила являются алгоритмами. Слово «алгоритм» в наши дни известно каждому, оно настолько уверенно шагнуло в разговорную речь, что сейчас нередко на страницах газет, в выступлениях политиков встречаются выражения «алгоритм поведения», «алгоритм успеха» и т.д.
В повседневной жизни каждый человек сталкивается с необходимостью решения задач самой разной сложности. Некоторые из них трудны и требуют длительных размышлений для поиска решений (а иногда его так и не удается найти), другие же, напротив, столь просты и привычны, что решаются автоматически. При этом выполнение даже самой простой задачи осуществляется в несколько последовательных этапов (шагов). В виде последовательности шагов можно описать процесс решения многих задач, известных из школьного курса математики: приведение дробей к общему знаменателю, решение системы линейных уравнений путем последовательного исключения неизвестных, построение треугольника по трем сторонам с помощью циркуля и линейки и т.д. Такая последовательность шагов в решении задачи называется алгоритмом. Каждое отдельное действие – это шаг алгоритма. Последовательность шагов алгоритма строго фиксирована, т.е. шаги должны быть упорядоченными. Правда, существуют параллельные алгоритмы, для которых это требование не соблюдается.
Понятие алгоритма близко к другим понятиям, таким, как метод (метод Гаусса решения систем линейных уравнений), способ (способ построения треугольника по трем сторонам с помощью циркуля и линейки). Можно сформулировать основные особенности именно алгоритмов:
-
Наличие исходных данных и некоторого результата. Алгоритм – это точно определенная инструкция, последовательно применяя которую к исходным данным, можно получить решение задачи. Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных. Например, в алгоритме деления вещественных чисел делимое может быть любым, а делитель не может быть равен нулю.
-
Массовость, т.е. возможность применять многократно один и тот же алгоритм. Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так алгоритм сложения применим к любой паре натуральных чисел.
-
Детерминированность. При применении алгоритма к одним и тем же исходным данным должен получаться всегда один и тот же результат, поэтому, например, процесс преобразования информации, в котором участвует бросание монеты, не является детерминированным и не может быть назван алгоритмом.
-
Результативность. Выполнение алгоритма должно обязательно приводить к его завершению. В то же время можно привести примеры формально бесконечных алгоритмов, широко применяемых на практике. Например, алгоритм работы системы сбора метеорологических данных состоит в непрерывном повторении последовательности действий («измерить температуру воздуха», «определить атмосферное давление»), выполняемых с определенной частотой (через минуту, час) во все время существования данной системы.
-
Определенность. На каждом шаге алгоритма у исполнителя должно быть достаточно информации, чтобы его выполнить. Кроме того, исполнителю нужно четко знать, каким образом он выполняется. Шаги инструкции должны быть достаточно простыми, элементарными, а исполнитель должен однозначно понимать смысл каждого шага последовательности действий, составляющих алгоритм (при вычислении площади прямоугольника любому исполнителю нужно уметь умножать и трактовать знак «x» именно как умножение). Поэтому вопрос о выборе формы представления алгоритма очень важен. Фактически речь идет о том, на каком языке записан алгоритм.
Для записи алгоритмов необходим некоторый язык, при этом очень важно, какой именно язык выбран. Записывать алгоритмы на русском языке (или любом другом естественном языке) громоздко и неудобно. Например, описание алгоритма Евклида для нахождения НОД (наибольшего общего делителя) двух натуральных чисел может быть представлен в виде трех шагов.
Пример 1
Алгоритм Евклида нахождения НОД двух натуральных чисел m и n:
Шаг 1: Если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае перейти на следующий шаг.
Шаг 2: Определить большее из чисел.
Шаг 3: Заменить большее из чисел разностью большего и меньшего из чисел.
Шаг 4: Повторить алгоритм со второго шага.
Приведенная здесь запись алгоритма нахождения НОД очень упрощенная. Запись, данная самим автором, Евклидом, представляет собой страницу текста, причем последовательность действий существенно сложней.
Одним из распространенных способов записи алгоритмов является запись на языке блок-схем. Запись представляет собой набор элементов (блоков), соединенных стрелками. Каждый элемент – это «шаг» алгоритма. Элементы блок-схемы делятся на два вида. Элементы, содержащие инструкцию выполнения какого-либо действия, обозначают прямоугольниками, а элементы, содержащие проверку условия – ромбами. Из прямоугольников всегда выходит только одна стрелка, а из ромбов – две (одна из них помечается словом «да», другая – словом «нет», они показывают, соответственно, выполнено или нет проверяемое условие).
Таблица 1
|
Название блока |
Обозначение и пример заполнения |
Пояснение |
|
Процесс |
|
Вычислительное действие или последовательность действий |
|
Решение |
|
Проверка условий |
|
Модификация |
|
Начало цикла |
|
Предопределенный процесс |
|
Вычисления по подпрограмме |
|
Ввод/вывод |
|
Ввод/вывод в общем виде |
|
терминатор |
|
Начало, конец алгоритма, вход и выход в подпрограмму |
|
Документ |
|
Вывод результатов на печать |
|
Соединитель |
|
Маркировка разрывов линий |
Последовательность действий обозначают линиями со стрелками на конце. Для простоты чтения схемы желательно, чтобы линия входила в блок сверху, а выходила снизу. Если линии идут не слева направо и не сверху вниз, то стрелка в конце линии обязательна, в противном случае ее можно не ставить.
Пример 2
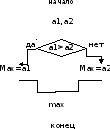
Алгоритма Евклида нахождения НОД двух чисел содержит две проверки условия: проверку на равенство чисел и если, числа не равны, то проверяется, какое из чисел больше.
Рисунок 1
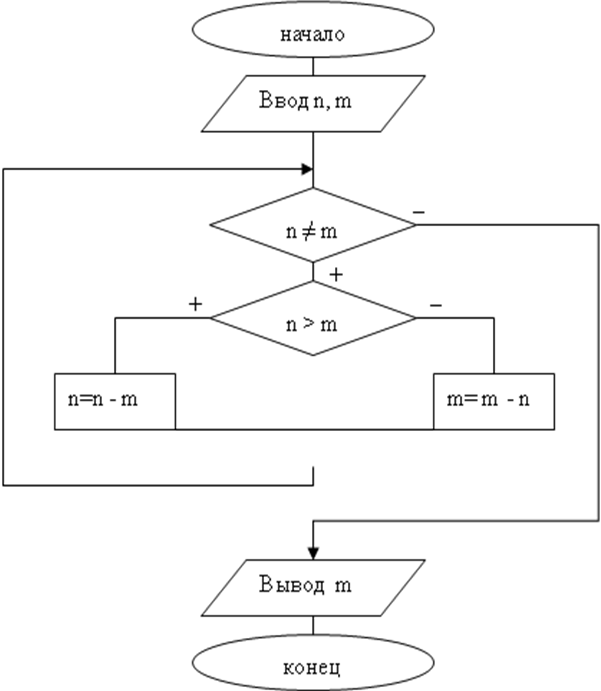
Построение блок-схем из элементов всего лишь нескольких типов дает возможность преобразовать их в компьютерные программы и позволяет формализовать этот процесс.
Из простых команд и проверки условий образуются составные команды, имеющие более сложную структуру и так же один вход и один выход. Эти команды представляют собой базовые алгоритмические структуры (конструкции): следование, ветвление, повторение, которые также должны быть оформлены стандартным образом (см. Таблица 2).
Таблица 2
|
Базовая структура |
Блок-схема |
Пример |
|
Следование Из команд следования образуются линейные алгоритмы. |
|
Определить синус выражения 5+1.2*x, где x вводится с клавиатуры.
|
|
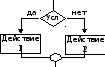
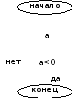
Ветвление Из команд следования и команд ветвления составляются разветвляющиеся алгоритмы (алгоритмы ветвления). |
Если Условие выполняется, то вычисляется Действие1, если Условие не выполняется, то вычисляется Действие2.
|
Найти наибольшее из двух чисел, введенных с клавиатуры.
|
|
Цикл с предусловием Повтор действий осуществляется при проверке условия. |
Сначала проверяется Условие, и если оно выполняется, то выполняется Действие. Затем снова проверяется Условие и т.д. до тех пор, пока Условие не выполнится. В этом случае выполняется следующий за циклом оператор.
|
Вводится последовательность положительных чисел. При вводе нуля или отрицательного числа ввод прекращается.
|
|
Цикл с постусловием
|
Сначала выполняется действие и лишь затем, проверяется условие. Причем действия повторяются до тех пор, пока условие не соблюдается (ложно).
|
Вводится последовательность ложительных чисел. При вводе нуля или отрицательного числа ввод прекращается.
|
С помощью соединения только этих элементарных конструкций можно "собрать" алгоритм любой степени сложности. Соединять простые и составные команды алгоритма можно двумя способами: последовательно и посредством вложения одной команды в другую (см. ).
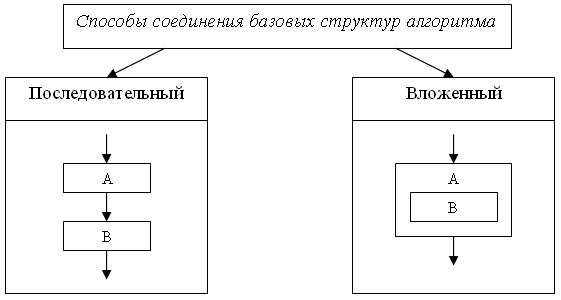
Рисунок 2
Пример
3
Пример алгоритма, который выводит квадраты чисел из интервала [a,b], вводимого с клавиатуры.
Два действия алгоритма - вывод квадрата числа и увеличение числа а на единицу, расположены внутри оператора цикла (выделенная область), т.е. являются вложенными в цикл.
Каждая указанная выше конструкция может быть без изменений в структуре реализована на любом языке программирования, например, на Паскаль или Бейсике. Поэтому необходимо грамотно составить алгоритм с помощью блок-схемы, а уже затем, зная, как записываются команды на конкретном языке программирования, набрать программу на компьютере и получить результат, запустив ее на исполнение.
Задания для самостоятельной работы
Задание 1.1
Опишите алгоритм вычисления площади треугольника по трем заданным сторонам словесно или на псевдокоде, а также с помощью блок-схемы.
Задание 1.2
Дано словесное описание алгоритма. Составить блок-схему данного алгоритма и определить, результат работы алгоритма.
1. Вводится натуральное число А.
2. Берется число b=2.
3. Если число А делится нацело на число b, то вывести b.
4. Число b увеличивается на единицу.
5. Если число b=А, то процесс прекратить, иначе перейти к пункту 3.
Задание 1.3
Дано словесное описание алгоритма. Составить блок-схему данного алгоритма и определить, результат работы алгоритма.
-
Вводятся два целых числа в переменные А и В.
-
Если А > В, то процесс прекратить.
-
В переменную А записать значение В.
-
Ввести новое число в переменную В.
-
Перейти к пункту 2.
Задание 1.4
С
помощью блок-схемы описать алгоритм
вычисления
значения функции
 .
.
Задание 1.5
Опишите алгоритм словесно или на псевдокоде, а также постройте блок-схему.
-
Составить алгоритм работы с банкоматом при получении денег с карточки.
-
Опишите алгоритм перехода через проезжую часть дороги.
-
Опишите алгоритм подготовки к экзамену.
Задание 1.6
Дано словесное описание алгоритма. Составить блок-схему данного алгоритма и определить, результат работы алгоритма.
Вводится массив из N чисел a1, a2,… an. Сравниваются два соседних элемента ai и ai+1. Если элемент ai > ai+1, то они меняются местами. Далее сравниваются следующие элементы ai+1 и ai+2, ai+2 и ai+3, …, an-1 и an. При втором обходе – длина массива уменьшается на 1 (исключается последний элемент) и процесс повторяется. Последний обход выполняется для массива из 2 элементов.
Задание 1.7
Cоставить алгоритм решения квадратного уравнения ax2+bx+c=0.
Вопросы для самоконтроля:
Вопрос 1. Определение алгоритма. Свойства алгоритма.
Вопрос 2. Перечислите базовые алгоритмические структуры.
Вопрос 3. Каким блоком изображается проверка условия в блок-схеме алгоритма?
Вопрос 4. В каких случаях на блок-схеме необходимо обязательно изображать стрелочки, а в каких можно опустить?
Вопрос 5. Из каких блоков состоит алгоритмическая циклическая структура?