Випадок, коли

Випадок, коли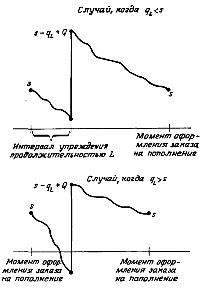

Інтервал випередження протяжністю l

Момент оформлення заказу на поповнення

Момент оформлення заказу на поповнення

Момент оформлення заказу на поповнення

Рис. 11.3. Пилкоподібні моделі управління запасами при стохастичному характері попиту:

q – попит протягом інтервалу попередження; Q – обсяг замовлення для поповнення запасів; s – критичний рівень запасів

Якщо при q_L > s виходити з того, що на усьому відрізку часу до надходження поповнення рівень запасів дорівнює нулю, то формула для витрат на утримання сильно ускладниться. Тому в якості математичного наближення допустимо, що при q_L > s рівень запасів стає рівним нулю у момент часу, що безпосередньо попереджає надходження поповнення. Тоді легко переконатися, що

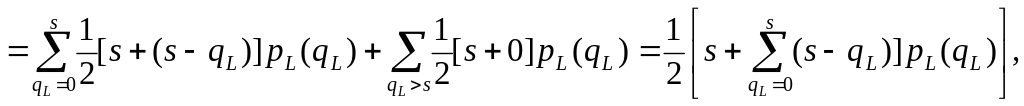(10)

(11)

Тепер потрібно знайти „зважене” значення виразу (10) шляхом його множення на величину M_L / Q, що представляє собою частку часу, протягом якого система функціонує в режимі чекання замовленої партії виробів і зважене значення виразу (11) шляхом його множення на величину (1 – M_L / Q).

Легко переконатися, що після виконання згаданих операцій і додавання отриманих у результаті їхнього виконання виразів прийдемо до наступної формули для очікуваного середнього рівня запасів на одиничному відрізку часу:

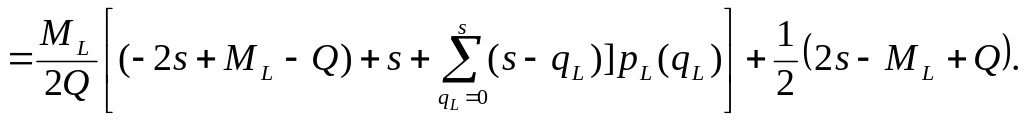(12)

Неважко показати, що

(13)

і, отже, праву частину співвідношення (12) можна записати у вигляді

(14)

Нарешті,

(15)

Множачи останній вираз на ваговий коефіцієнт M/Q, приходимо до виразу для очікуваного обсягу недостачі в розрахунку на одиницю часу (яке аналогічно відповідному виразу в моделі ЕВРП, розглянутої у попередньому розділі).

Складаючи вираз (9), помножений на h вираз (14), а також помножений на π ∙ M/Q вираз (15), одержимо наступну формулу:

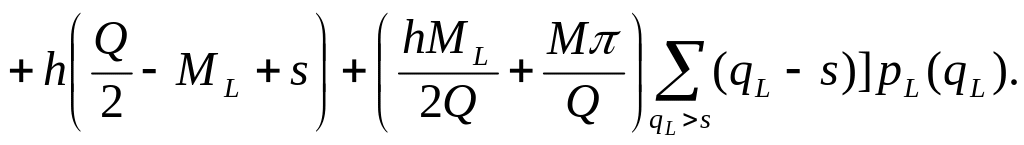(16)

Щоб зрозуміти характер взаємозв’язку між формулою (16) і відповідними формулами, приведеними у попередньому розділі, помітимо, що якби попит був детермінованим, то критичний обсяг запасів дорівнював би M_L (s = M_L), а сума в правій частині (16) звернулася б у нуль, тому що мала б місце тотожність .

Обчисливши часткову похідну дЕ[AС]/дQ, дорівнявши її нулю та вирішивши отримане в результаті рівняння відносно Q, прийдемо до наступної формули:

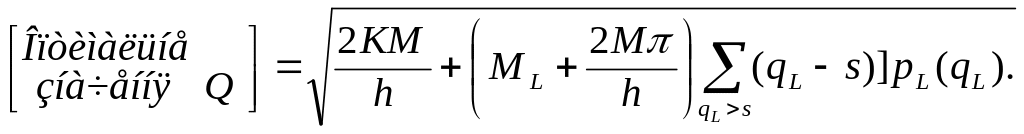(17)

Визначимо статистичний розподіл для попиту наступним виразом:

(18)

Тоді можна показати, що оптимальне значення s(s ≥ 0) є найменше з цілих чисел, що задовольняють умові

P_L (s) > R (визначення критичного рівня), (19)

Величину R можна назвати граничним коефіцієнтом, або граничним показником,

де 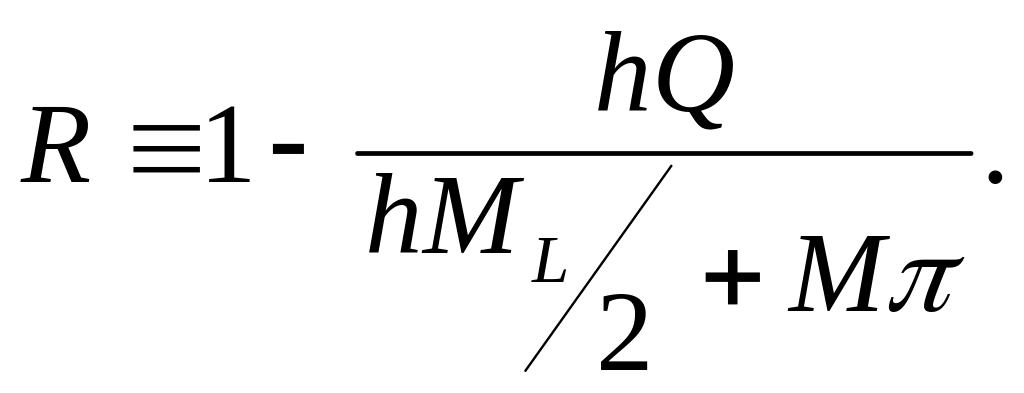(20)

Точніше це можна сформулювати так: обсяг замовлення Q і критичний рівень запасів s є оптимальними, якщо вони одночасно задовольняють (17) та (19). Підставляючи (17) у (16), одержуємо

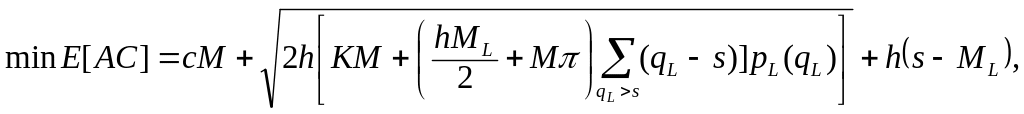(21)

де s знаходиться з умови (19). Помітимо, що через наявність у (17) члена під знаком кореня оптимальне значення Q стає більшим у порівнянні з оптимальним значенням Q у випадку детермінованого попиту. Звернемо також увагу на те, що при зменшенні значення s значення Q зростає. Так само легко переконатися й у тому, що чим більше значення Q, тим менше значення обумовленого формулою (20) значення R і тим нижче значення s, при якому починає виконуватися умова (19). Значення P_L(у) при у = s іноді називають рівнем обслуговування, а значення у – Е[q_L] при y = s – буферним, або гарантійним запасом.

Алгоритмічний метод рішення. Нижче дається опис досить простої процедури, за допомогою якої обчислюються значення Q та s, одночасно задовольняючим умовам (17) і (19):

Крок 1. Покладіть початкове спробне значення Q рівним (2 КМ / h)^1/2.

Крок 2. Обчисліть R за формулою (20), використовуючи поточне спробне значення Q, а потім з умови (19) знайдіть відповідне спробне значення s.

Крок 3. Припиніть обчислення, якщо нове спробне значення s збігається з попереднім. У супротивному випадку за допомогою (17) обчисліть нове спробне значення Q, після чого поверніться до кроку 2.

Помітимо, що на кожній наступній ітерації спробні значення s зменшуються, а спробні значення Q зростають. У випадку, коли оптимальне значення s є позитивним, розглянутий метод рішення завжди забезпечує збіжність за кінцеве число ітерацій. Для збіжності досить виконання наступної умови:

(22)

де є виразом, що стоїть в правій частині співвідношення (17) при s = 0. Знову підкреслимо, що, оскільки щодо виду ніяких припущень, крім постулату дискретності, не приймалося, глобальність оптимуму для s не гарантована; проте завжди можна бути упевненим в тому, що у випадку, коли знайдений оптимум не є абсолютним, більш оптимальне рішення лежить у найближчій околиці раніше обчисленого значення s та відповідного йому значення Q.

Розглянемо приклад, що характеризується вихідними даними, що збігаються з чисельними значеннями, приведеними в (5) і (7), тобто припустимо, що

с = 1, К = 31,25, h = 5, π = 20, L = 1,

q = 0, 1, …, 4, (23)

Відповідно до кроку 1:

Початкове спробне значення Q = 5. (24)

Тоді, реалізуючи крок 2, одержуємо

та Р(2) ≥ 0,44. (25)

Для спробного значення s = 2, відповідно до кроку 3, знаходимо спробне значення

(26)

Повторивши процедури, запропоновані кроками 2 і 3, будемо мати R = 0,34 та Р (1) ≥ 0,34, а спробне значення

(27)

На заключній ітерації R = 0,24 та Р (1) ≥ 0,24, а оптимальне значення s = 1. При цьому:

Оптимальне значення Q = 6,83;

Оптимальне значення S = s + Q = 7,83, (28)

і, отже,

min Е [АС] = (29)

Апроксимація, заснована на використанні нормального розподілу. Кожного разу, коли розглянута у даному розділі модель використовується для аналізу мультитоварних систем управління запасами, , як правило, апроксимується будь-яким конкретним розподілом імовірностей (пуассонівським, біноміальним, рівномірним тощо). Коли тип розподілу визначений, залишається лише задати чисельні значення відповідних параметрів. Дуже зручним виявляється використання нормального розподілу, що є безперервним, із середнім значенням і дисперсією вигляду:

(30)

Такий метод апроксимацій виявляється з практичної точки зору винятково ефективним, незважаючи на те, що математичні властивості нормального розподілу (такі, як наявність симетрії, допустимість як завгодно малих, а також як завгодно великих значень випадкової перемінної тобто) можуть істотно відрізнятися від . Зрозуміло, що перш ніж використовувати зазначений (або якийсь інший) спосіб наближеного опису необхідно дослідити, наскільки він адекватний реальному розподілу в тому діапазоні значень параметрів, що становить інтерес у розглянутому випадку.

Введемо до розгляду величину

(31)

так що

(32)

Нехай, як і в попередньому випадку,

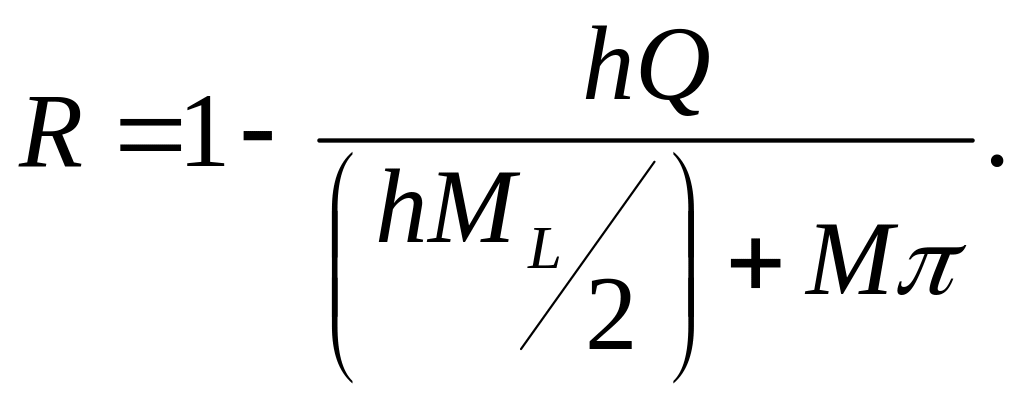(33)

Позначимо нормовану функцію нормального розподілу імовірностей через

(34)

а так називану нормовану інтегральну функцію втрат, що відповідає нормальному розподілу (34), – через

(35)

де значення та для ряду значень и приведені в табл. 11.1.

Використовуючи функцію втрат (35) та дані табл. 11.1, можемо написати наступну наближену рівність:

(36)

У такому випадку для визначення u_s замість умови (19) використовується співвідношення

(37)

Таблиця 11.1

Значення функцій та у випадку

нормального розподілу

u
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0	0,5000 0,5399 0,5793 0,6180 0,6555 0,6915 0,7258 0,7581 0,7882 0,8160 0,8414 0,8644 0,8850 0,9032 0,9193 0,9332 0,9453 0,9555 0,9641 0,9713 0,9773 0,9822 0,9861 0,9893 0,9919 0,9938 0,9954 0,9966 0,9975 0,9982 0,9987	0,3989 0,3509 0,3068 0,2667 0,2304 0,1977 0,1686 0,1428 0,1202 0,1004 0,0833 0,0686 0,0561 0,0455 0,0366 0,0293 0,0232 0,0182 0,0142 0,0110 0,0084 0,0064 0,0048 0,0036 0,0027 0,0020 0,0014 0,0010 0,0007 0,0005 0,0003	0,5000 0,4601 0,4207 0,3820 0,3445 0,3085 0,2742 0,2419 0,2118 0,1840 0,1586 0,1356 0,1150 0,0968 0,0807 0,0668 0,0547 0,0445 0,0359 0,0287 0,0227 0,0178 0,0139 0,0107 0,0081 0,0062 0,0046 0,0034 0,0025 0,0018 0,0013	0,3989 0,4509 0,5068 0,5667 0,6304 0,6977 0,7686 0,8428 0,9202 1,0004 1,0833 1,1686 1,2561 1,3455 1,4366 1,5293 1,6232 1,7182 1,8142 1,9110 2,0084 2,1064 2,2048 2,3036 2,4027 2,5020 2,6014 2,7010 2,8007 2,9005 3,0003

а для обчислення оптимального значення Q замість (17) використовується формула

(38)

Алгоритм пошуку оптимального рішення виглядає так:

Крок 1. Знаходиться початкове спробне значення Q, що передбачається рівним (2KM / h)^1/2.

Крок 2. По формулі (33) для даного спробного значення Q обчислюється R, після чого за допомогою (37) визначається відповідне спробне значення u_s і за допомогою (32) – спробне значення s.

Крок 3. Якщо нове спробне значення s приблизно збігається з попереднім, обчислювальна процедура закінчується. У супротивному випадку за формулою (38) обчислюється нове спробне значення Q, після чого повертаються до кроку 2. Варто помітити, що для реалізації кроку 3 необхідно кількісно визначити „допуск”, тобто інтервал, у межах якого два спробні значення s вважаються приблизно співпадаючими.

Як ілюстрацію побудованого вище алгоритму розглянемо випадок, коли

К = 32, h = 1, π = 9, L = 1, М = M_L = 16, V_L = 48. (39)

Виконавши обчислення кроку 1, одержуємо

Початкове значення Q = 32, (40)

а в результаті реалізації кроку 2 знаходимо

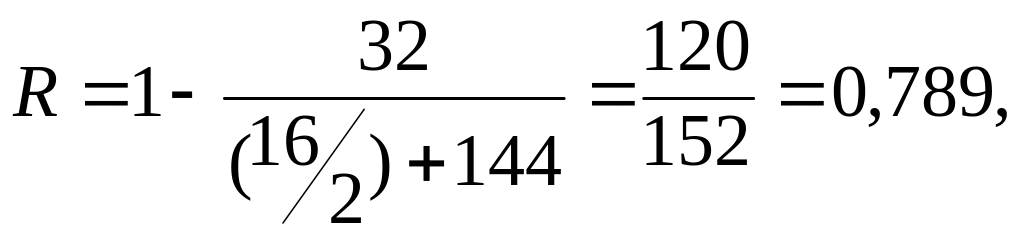(41)

так що відповідно до табл. 19.6:

Спробне значення u_s = 0,8, (42)

Спробне значення s = 16 + 0,8 √48 = 21,6.

Потім на кроці 3 одержуємо

Спробне значення Q =

(43)

Повертаємося до кроку 2 і знаходимо

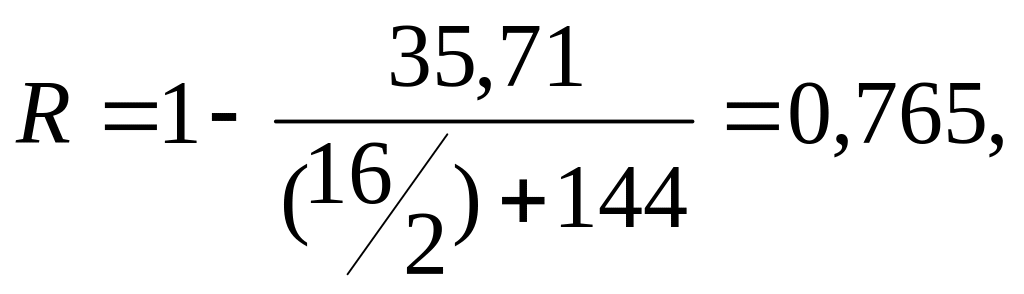(44)

і, таким чином:

Спробне значення u_s = 0,72, (45)

Спробне значення s = 16 + 0,72 √48 = 21,01.

Тоді на кроці 3 маємо

Спробне значення Q =

(46)

Наступні ітерації приведуть до спробних значень s та Q, що відрізняються від значень (45) і (46) лише „у дрібній частині”.

Для відповідної величини очікуваних витрат одержимо

Е [АС] = с16 + 41,3. (47)

Варто звернути увагу на те, що збільшення чисельного значення кожного з параметрів π, К, М, L та V_L приводить до одночасного збільшення оптимальних значень s та Q; виключенням є випадок зменшення Q при зростанні π і випадок зменшення s при зростанні К. Така залежність оптимальної стратегії від вибору чисельних значень показників, що фігурують у моделі, спостерігається лише у випадку, коли, відповідно до нормальному розподілу, що апроксимує величину , імовірність негативних значень q дуже мала, що має місце в тих випадках, коли . Відзначимо також, що оптимальне значення Q, знайдене викладеним вище методом, може у значній мірі перевищити аналогічний показник, обчислений за допомогою моделі ЕВРП; але навіть у цих випадках для знаходження оптимального рішення потрібно усього 3 – 4 ітерації.