
физика Литвинова н. н. электромагнетизм конспект ответы ВОЛНОВАЯ ОПТИКА / Общие правила выполнения ЛР
.pdf
vk.com/club152685050
К достоинствам этого метода, несомненно, следует отнести его простоту и наглядность. Его недостатками являются отсутствие корректной процедуры оценки погрешностей и необходимость вручную проводить экспоненту. Проведенный вручную график функции часто слишком тяготеет к отдельным экспериментальным точкам. Второй метод свободен от этих недостатков, но более громоздок.
Метод 2. Получившиеся значения f логарифмируются; на графике откладывается набор точек lnf от t, как это показано на рис. 6. Теоретически эта зависимость должна оказаться линейной
lnf =ln A−(1τ) t, |
(21) |
поэтому через экспериментальные точки нужно провести прямую линию по уже знакомым правилам.
Определив по графику длину отрезка lnА, отсекаемого прямой на оси ординат, найдем параметр А уравнения (21). Экстраполируя, т. е. продолжая получившуюся линию до пересечения с осью абсцисс, находим время t0, угловой коэффициент k = tgα и постоянную времени τ:
τ = |
t0 |
. |
(22) |
|
|||
|
ln A |
|
|
Отметим, что по оси ординат около каждой точки откладывается систематическая погрешность не самой величины f, а ее логарифма
θln f = |
θf |
(23) |
∆f |
Достоинством этого метода является то, что через набор точек нужно проводить не экспоненту “твердым движением руки”, а пря-
lnf
k = tgα = ln A t0
lnA
α 
t0 t
Рис. 6. Определение параметров уравнения (20)
21
vk.com/club152685050
мую линию – по линейке. Эта линия опирается сразу на весь набор экспериментальных точек. Вторым важным достоинством описанного метода является возможность оценить погрешности найденных параметров.
Систематическую погрешность величины А разумно принять равной значению систематической погрешности θf для значений, полученных при наименьшем значении времени t
θА = θf при mint. |
(24) |
Систематическую погрешность величины τ следует принять равной
|
θ |
θ |
A |
|
|
θτ = τ |
t + |
|
|
(25) |
|
|
|
||||
t0 |
A lnA |
|
|||
Оценка случайных погрешностей SА и Sτ:
–по имеющемуся набору точек проводят еще одну прямую;
–для нее находят новые значения величин А’ и τ’;
–принимают SА = А – А’ , а Sτ = τ – τ’ .
Описанная выше процедура графического определения углового коэффициента (тангенса угла наклона) применима к линейной функции. Если требуется найти угловой коэффициент для нелинейной функции, то он будет разным при разных значениях аргумента. Поэтому ищут угловой коэффициент касательной в интересующей точке. Эта процедура называется графическим дифференцированием. Она описана далее.
ГРАФИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
К графическому определению производной прибегают тогда, когда аналитическое выражение для функции неизвестно, и она задается графически (например, на основании измерений). Графическое определение производной называется графическим дифференцированием.
Поясним, как выполнить графическое дифференцирование. Известно, что производная от функции y = f(x) равна угловому коэффициенту касательной, построенной к кривой f(x) при том же самом значении аргумента x, при котором вычисляется dy/dx (рис. 7). Поэтому после графического отображения экспериментальной кривой для вычисления производной в некоторой точке достаточно прове-
22

vk.com/club152685050
y 
 ∆y
∆y
∆x
 ∆y
∆y
∆ x
∆y
∆x |
x |
Рис. 7. Графическое дифференцирование
сти на графике касательную к кривой в этой точке и вычислить ее угловой коэффициент. Производная тогда найдётся по формуле
y′= |
∆y |
|
∆x. |
(26) |
Здесь y и x – длины отрезков в единицах величин x и y, отложенных по осям. Эти элементы не должны быть всюду одними и теми же. Их нужно выбирать меньшими там, где функция изменяется быстрее.
Точность метода графического дифференцирования зависит от точности построения исходной кривой. Поэтому экспериментальную кривую, которую в дальнейшем планируется дифференцировать, нужно строить очень тщательно. Описанная процедура совпадает с методикой графического определения тангенса угла наклона линейной зависимости f(x) = k x + b, описанной в прошлом разделе.
ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ
x2
Определенный интеграл ∫ f(x)dx от неотрицательной функции
x1
f(x) может быть найден как площадь криволинейной трапеции под
23

vk.com/club152685050
y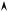
x1 |
x2 |
x |
Рис. 8. Графическое интегрирование
кривой f(x) на промежутке [x1 x2]. Такое представление удобно при вычислении интеграла от любой экспериментальной зависимости. Площадь фигуры – количественное значение интеграла – находят подсчетом составляющих ее клеток миллиметровки с умножением результата на масштаб по каждой оси.
Графическое интегрирование можно использовать, например, при определении пути, пройденного телом при сложном характере движения. Путь находят интегрированием экспериментальной кривой, отображающей зависимость скорости тела от времени
t2
S = ∫υdt. t1
Аналогично можно найти работу, совершенную газом в ходе сложного процесса, откладывая по оси x объем газа, а по оси y – давление
V2
A = ∫ pdV.
V1
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Часто экспериментально определяются величины x и y, связанные функциональной зависимостью
у = f(x, A, B, …). |
(27) |
Вид этой функции бывает обычно известен из физических законов, а коэффициенты A, B, …должны быть определены по результатам эксперимента (табл. 1).
24

vk.com/club152685050
|
|
|
|
|
|
Таблица 1 |
|
|
|
|
|
|
|
|
|
x |
x1 |
x2 |
x3 |
x4 |
…… |
|
xn |
y |
y1 |
y2 |
y3 |
y4 |
….... |
|
yn |
Практически вид приближающей функции можно определить визуально: по табл. 1 строится точечный график функции, а затем проводится кривая, наилучшим образом отражающая характер расположения точек (рис. 9). По этой кривой устанавливается вид приближающей функции (обычно из числа простейших аналитических функций: линейная, степенная, экспоненциальная или показательная, логарифмическая и т. д.). Чтобы формула не оказалась слишком сложной, число параметров не должно быть велико. Обычно берут два-три параметра. При сравнении обращают внимание на наличие максимумов и минимумов, поведение функции при больших и малых значениях аргумента, выпуклость кривой вверх или вниз на отдельных участках и т. д. Выбрав подходящую функцию, подбирают такие значения ее параметров, чтобы разница между опытными значениями величины и значениями, найденными по формуле, не превышала ошибок эксперимента. Если эта разница получается слишком большой, берут другой подходящий график и повторяют попытку.
y 
x
Рис. 9. Построение функции методом наименьших квадратов
Формула (27) называется эмпирической формулой или уравнением регрессии y на x и позволяет находить значения функции f(x) для нетабличных значений x, «сглаживая» результаты измерений величины y.
25
vk.com/club152685050
Рассмотрим частный случай, когда зависимость y от x линейная
у = b + kx. |
(28) |
В этом случае для нахождения b и k достаточно двух абсолютно точных измерений величин x и y. В действительности, измеренные экспериментальные значения xi и yi содержат ошибку, поэтому, по ним можно получить только оценки параметров функции b и k.
Чтобы получить достоверные оценки, производят многократные изменения. Получается набор из пар значений {xi, yi} (табл. 1). Нужно подобрать такие значения параметров b и k, чтобы рассчитанные значения функции в узлах {xi,} как можно меньше отличались от табличных значений {yi}. Просуммируем квадраты отклонений рассчитанной функции (28) от экспериментальных значений.
F(k,b) = ∑(b+kx −y )2. |
(29) |
i i |
|
При оптимальных значениях коэффициентов b и k функция (29) будет иметь минимум. Ищем его, приравнивая нулю частные производные этой функции по параметрам k и b:
∂∂F = ∑n 2(b+kxi −yi) =0, b i=1
∂∂F = ∑n 2(b+kxi −yi)xi =0. k i=1
Таким образом, для искомых коэффициентов получаем систему уравнений
b n +k∑x = ∑y |
|||
|
|
i |
i |
|
|
+k∑x2 |
= ∑y x |
b∑x |
|||
|
i |
i |
i i |
Решая эту систему относительно b и k, получаем следующие выражения
|
∑x2 |
∑y −∑x ∑x y |
|
|
n∑x y −∑x ∑y |
|
||||
b= |
i |
i |
i i |
i |
|
k= |
i i |
i i |
|
|
n∑(xi2 )−(∑xi )2 |
|
, |
|
. |
(30) |
|||||
|
n∑(xi2 )−(∑xi )2 |
|||||||||
Функция (28) с этими значениями коэффициентов b и k наилучшим образом соответствует всему массиву экспериментальных данных.
Метод наименьших квадратов позволяет также оценить погрешности найденных значений параметров b и k:
26
vk.com/club152685050
|
|
|
|
S |
∑x2 |
|
|
|
|
|
|
S |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||||||
|
|
Sb = |
|
y |
|
i |
|
, |
Sk = |
|
|
y |
|
|
|
|
|
, |
(31) |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
n∑(xi2 )−(∑xi )2 |
n∑(xi2 )−(∑xi )2 |
||||||||||||||||||
|
|
n∑(yi2 )−(∑yi )2 |
|
|
(n∑x y −∑x |
∑y )2 |
|
|
|
|
|
|
|
||||||||
где Sy2 |
= |
|
|
|
|
− |
|
|
|
|
i i |
i |
i |
|
|
|
. |
|
|
|
|
n(n−2) |
|
|
|
|
2 |
|
2 |
) |
|
|
|
||||||||||
|
|
|
|
|
|
|
n(n−2)(n∑(xi |
)−(∑xi ) |
|
|
|
|
|
||||||||
Если числители и знаменатели в формулах (31), (32) разделить на n2, то все величины можно вместо сумм выразить через средние значения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b= |
x2 |
y |
− |
x |
|
|
|
xy |
|
, |
|
|
k= |
|
|
xy |
− |
x |
|
y |
|
. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
−( |
|
)2 |
|
|
|
|
|
|
−( |
|
)2 |
|
|||||||||||||||||||||||||
|
|
|
x2 |
x2 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sb2 = Sk2 (x2 ), |
|||||||||||||||||||||
|
|
|
|
Sk2 |
= |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
−( |
|
)2 |
||||||||||||||||||||||||||||||||||
|
|
|
(x2 ) |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
2 |
|
|
|
(xy−x y) |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
где Sy2 |
= |
|
y2 |
−(y) |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
(n−2) |
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−(x) |
|
|||||||||||||||||||||||||||||
(30а)
(31а)
Смотри примеры [11–14] обработки результатов измерений методом наименьших квадратов в прил. 2.
Рекомендованная литература
1. Зайдель А. Н. Ошибки измерений физических величин. Л.: Наука. 1985. 181 с.
2. Худсон Д. Статистика для физиков. М.: Мир. 1970. 296 с. 3. Деденко Л. Г., Керженцев В. В. математическая обработка и
оформление результатов эксперимента. М.: Изд. МГУ, 1977. 112 с.
27
vk.com/club152685050
Приложение 1
Примеры вычислений погрешностей
Пример 1
Электрический ток через лампу измеряется амперметром, в диапазоне до Im = 3 A и классом точности KI = 1. Падение напряжения на лампе измеряется вольтметром с пределом измерения Um = 10 B и классом точности KU = 2. Показания приборов: I = 1,27 A, U = 6,2 B. Найти мощность, потребляемую электрической лампой, и ее систематическую погрешность.
Решение. Электрическая мощность вычисляется по известной формуле P = U · I. Это выражение обозначает, что электрическая мощность P является функцией двух непосредственно измеряемых величин: P = P (U, I). Систематические погрешности прямых измерений тока и напряжения находятся по формуле (1а):
θ |
I |
= |
Im KI |
= |
3 1 |
= 0,03 ( A); θ = |
Um KU |
= 10 2 |
= 0,2 |
( B). |
|
|
|
||||||||
|
100 |
100 |
U |
100 |
100 |
|
|
|||
|
|
|
|
|
||||||
Поскольку мы имеем дело с косвенным измерением функции P, систематическую погрешность сопротивления θP можно выразить через погрешности тока θI и напряжения θU при помощи формулы (2):
θ |
|
= |
|
∂P |
|
θ |
|
+ |
|
∂P |
|
θ . |
|
|
|
|
|
|
|||||||
|
|
∂I |
|
|
∂U |
|||||||
|
R |
|
|
|
|
I |
|
|
|
U |
Найдем частные производные от сопротивления по току и по на-
пряжению: |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂P |
= |
∂(IU) |
= I |
∂U |
= I, |
∂P |
= |
∂(IU) |
= U |
∂I |
= U. |
|
∂U |
∂U |
∂U |
∂I |
∂I |
∂I |
||||||
|
|
|
|
|
|
|
||||||
Таким образом, получаем окончательное выражение для систематической погрешности электрического сопротивления:
θP = IθU +UθI;
θP =1,27 0,2+6,2 0,03=0,25+0,19=0,44=0,5 ( Âò).
Теперь найдем |
электрическую мощность и |
округлим ее |
до десятых – так |
же, как и систематическую |
погрешность |
P= I U =1,27 6,2=7,9 ( Âò).
Ответ: Р = (7,9±0,5) Вт.
28

vk.com/club152685050
Пример 2
Проводится косвенное измерение горизонтальной составляющей напряженности магнитного поля Земли. Для этого с помощью витка с током, ориентированного вдоль магнитного меридиана, создается магнитное поле, перпендикулярное полю Земли. В центр витка помещается компас, стрелка которого показывает направление напряженности результирующего поля. Тангенс угла отклонения стрелки равен отношению напряженности магнитного поля витка к напряженности внешнего магнитного поля
tgα = |
Hвитка |
= |
IN |
. |
|
H |
|
2R H |
|
|
Земли |
|
Земли |
|
В этой формуле I – ток, R = 0,2 м – радиус витка, N = 36 – количество витков провода. Класс точности миллиамперметра K = 1,0, диапазон измерений – Imax = 200 мА. Систематическая погрешность измерения тока
θI = K100Imax = 1100200 =2(ìÀ) =0,002(À).
Компас класса точности не имеет, систематическая погрешность измерения угла составляет половину градуса.
Результаты прямых измерений: I = (80 ± 2) мА, α = 34,0° ± 0,5°. В международной системе единиц угол измеряется не в граду-
сах, а в радианах
θα =0,5° 180πðàä° =0,009ðàä.
Решение. Горизонтальную составляющую напряженности магнитного поля Земли находим по формуле
= IN ctgα
HЗемли 2R .
Таким образом, НЗ = НЗ(I, α) является функцией двух переменных, тока I и угла α отклонения стрелки компаса. Систематическая погрешность θН выражается через систематические погрешности θI и θα.
|
∂HЗемли |
|
|
∂HЗемли |
|
|
θI. |
|
θH = |
|
θα + |
|
|||||
∂α |
∂I |
|||||||
|
|
|
|
|||||
Сначала вычислим частные производные по этим переменным.
29

vk.com/club152685050
∂HЗемли = |
IN |
|
∂ctgα |
= |
IN |
|
1 |
. |
∂α |
2R |
|
∂α |
|
2R |
|
sin2 α |
|
Домножаем числитель и знаменатель этого выражения на cosα и учитываем, что 2sinα · cosα = sin2α.
∂HЗемли |
= |
IN cosα |
|
1 |
|
= |
IN |
ctgα |
1 |
= |
2HЗемли |
. |
|||||
|
|
|
sinα cosα |
R |
sin2α |
|
|||||||||||
∂α |
2R sinα |
|
|
|
sin2α |
||||||||||||
|
|
|
∂HЗемли |
= |
N ctgα |
= |
|
HЗемли |
. |
|
|
|
|||||
|
|
|
∂I |
2R |
|
|
|
I |
|
|
|
|
|
||||
Получаем окончательную формулу систематической погрешности θН
θ |
H |
= H |
|
2θα |
+ |
θI . |
|
|
|
||||||
|
Земли |
|
|
I |
|
||
|
|
|
sin2α |
|
|
||
Вычисления: |
|
|
|
|
|
|
|
|
|
|
|
H |
|
= 0,08 36 ctg34° |
=10,7 |
( |
À ì. |
||||||
|
Земли |
|
|
2 0,2 |
|
|
|
|
) |
||
|
|
|
|
|
|
|
|
|
|
|
|
θ |
|
=10,7 |
2 |
0,009 + |
2 |
= 0,5 |
( |
|
À ì. |
||
H |
|
|
|
|
|||||||
|
|
|
|
|
0,93 |
80 |
|
|
|
|
|
Ответ: НЗемли = (10,7 ± 0,5) А/м.
Пример 3
В микроскоп наблюдаются Кольца Ньютона в отраженном свете. Измеряются радиусы двух темных колец – второго и седьмого (r2 и r7). По этим данным и по длине волны света находится радиус кривизны линзы. Результаты измерений и данные с установки:
r2 = (0,230±0,005) ìì, r7 = (0,550±0,005) ìì, λ = 0,6 ìêì.
Радиус линзы связан с радиусами колец и длиной волны формулой
R = rk2 −rm2 , где k = 7, m = 2.
λ(k−m)
Решение. В данном случае вычисленный радиус линзы R является функцией R = R(rk, rm). Систематическая погрешность θR выражается через погрешности радиусов, и через значения частных производных функции R по обеим переменным. Сначала найдем эти производные.
30
