Прочность соединения

Как было указано выше, стандартную посадку выбирают по ус­ловиям неподвижности соединения при заданной нагрузке без каких-либо дополнительных скреплений. Однако возможны, случаи, когда намеченная посадка недопустима по условиям прочности сопряга­емых деталей, так как ее натяг вызывает их разрушение или чрез­мерные деформации.

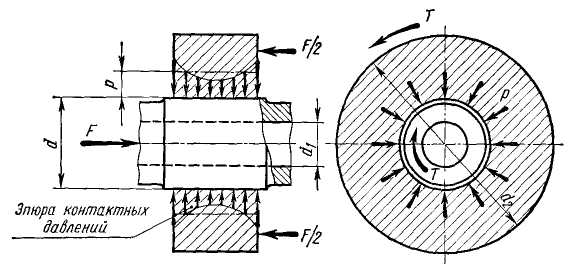
Рис. 10.3. Расчётная схема соединения с натягом.

Поэтому при расчете прессованных посадок необходимо рассматривать как условия прочности (неподвижности) соединения, так и условия прочности деталей. Расчет прочности деталей является провер­кой возможности приме­нения намеченной посадки.

Расчет прочности со­единения. На рис. 10.3 приведена расчетная схе­ма прессового соединения.

Условие прочности со­единения при нагружении осевой силой

, (10.2)

где р — давление на поверхность контакта; К ~1,5...2 — коэффициент запаса.

Условие прочности соединения при погружении крутящим момен­том

(10.3)

При совместном действии Т и F_a

<fpπdl, (10.4)

где F_t = 2T/d — окружная сила, F_a – осевая сила.

По теории расчета толстостенных цилиндров, изучаемой в курсе сопротивления материалов, удельное давление на поверхности кон­такта связано с натягом зависимостью [8]

p = , (10.5)

где N — расчетный натяг; С ₁ и С₂ — коэффициенты;

; ,

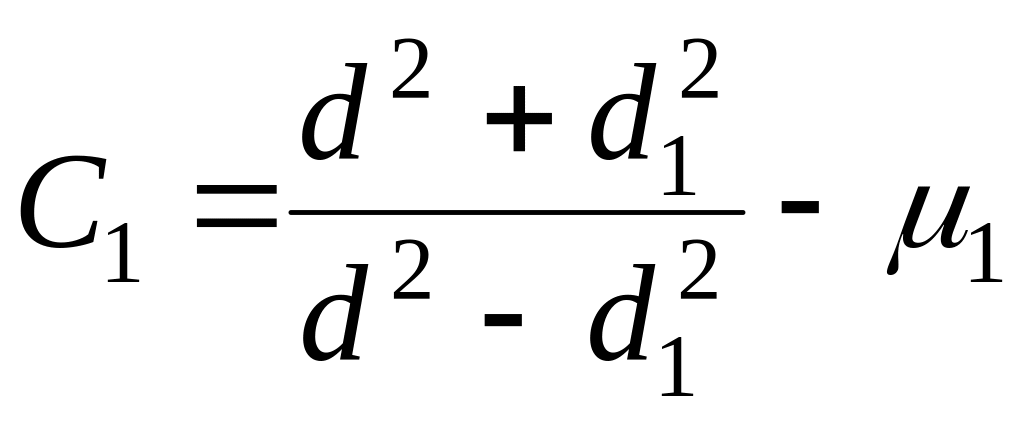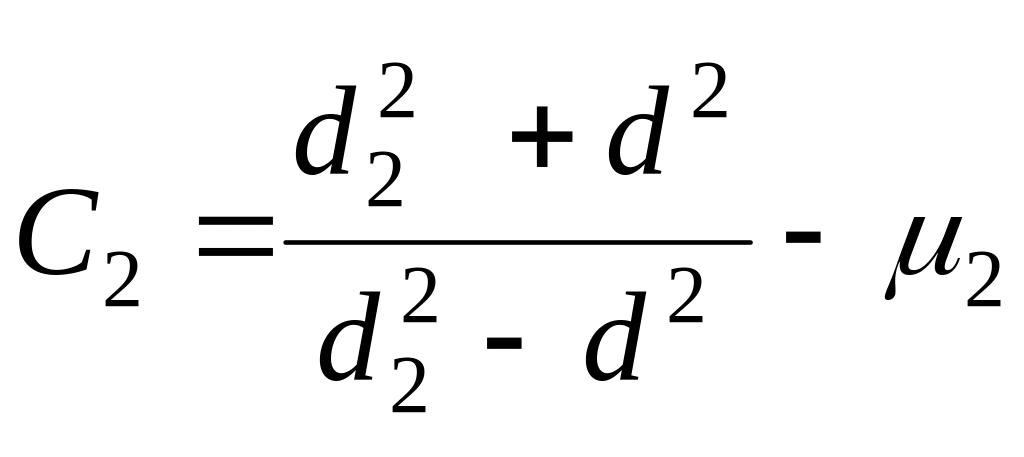E₁ и Е₂, и — модули упругости и коэффициенты Пуассона ма­териалов вала и втулки: для стали и , для чугуна и , для бронзы и .

При расчете прочности соединения расчетный натяг N опреде­ляют по минимальному табличному или вероятностному натягу с поправкой и на срезание и сглаживание шерохова­тости поверхности при запрессовке (если сборку выполняют нагре­ванием или охлаждением, u = 0):

N = N_min—u, u = (R_z1 +R_z2 ), (10.6)

где R_z1 и R_z2 - высоты шероховатостей посадочных поверхностей

В этой формуле не учитывается возможное изменение натяга в случае различия в коэффициентах температурного линейного расширения деталей.

Наиболее распространенные значения R_г для поверхностей прессовых соеди­нений: 10...6,3;

Рис. 10.4 3,2...1,6 мкм, что соответствует 6...8-му классам шероховатости.

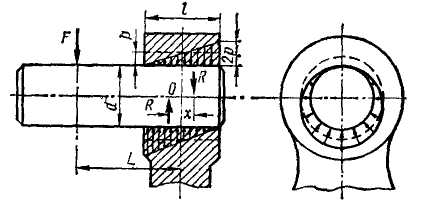
Изгибающий момент, которым может быть нагружено соедине­ние, определяют на основе следующих расчетов (рис. 10.4).

Действие момента (M=FL) вызывает в соединении такое перераспределение давления р, при котором внешняя нагрузка уравновешивается мо­ментом внутренних сил M*R = R*x.

Составляя расчетные зависимости, полагают, что поворот шипа происходит вокруг центра тяжести соединения — точки O, а перво­начальная равномерная эпюра давлений (на чертеже показана штри­ховой линией) переходит в треугольную, как показано на рис. 10.4, или трапецеидальную. Кроме того, не учитывают действие силы F, перенесенной в точку О, как малое в сравнении с действием момента М. Максимально давление изменяется в плоскости действия нагрузки. При некотором значении нагрузки эпюра давления из трапеции превращается в треугольник с вершиной у края отверстия и осно­ванием, равным 2р. Этот случай является предельным, так как даль­нейшее увеличение нагрузки приводит к появлению зазора (раскрытие стыка). Учитывая принятые положения, можно написать:

M = FL = Rx, где R — равнодействующая давлений на поверхностях верхнего и нижнего полуцилиндров. Значение этой равнодействующей опре­деляется давлением р прессовой посадки и не изменяется от действия изгибающего момента

R=pld. Плечо пары х=1/3.

Подставляя, получаем F = pdl²/3.

Для обеспечения необходимого запаса прочности соединения на практике принимают . (10.7)

При этом давление в наиболее нагруженных точках соединения не должно взывать пластических деформаций.