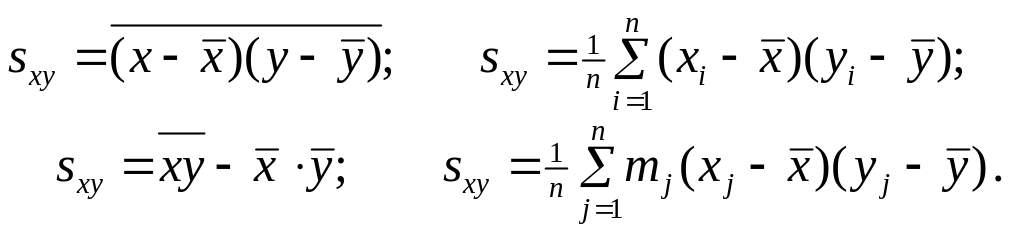Контрольні питання з відповідями

1. Перелічити основні характеристики генеральної сукупності і їх вибіркові оцінки (центр угруповання, міра мінливості, функції розподілу).

   Генеральная совокупность	Выборочные оценки
   р – вероятность	– относительная частота (частость)
   М(х) – математическое ожидание, центр совокуп­ности, генеральное сред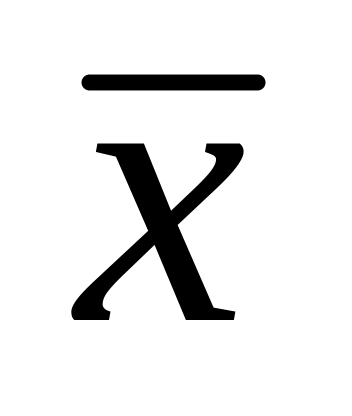нее	= Хср – центр выборки, выборочное среднее (просто «среднее»)
   D(x) = 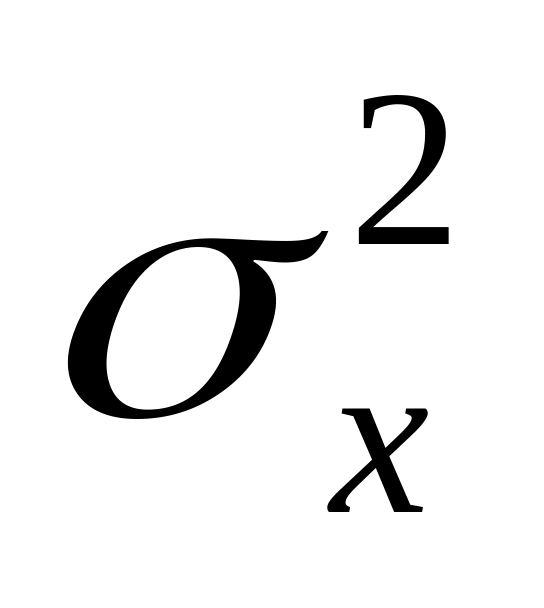– дисперсия, мера изменчивости	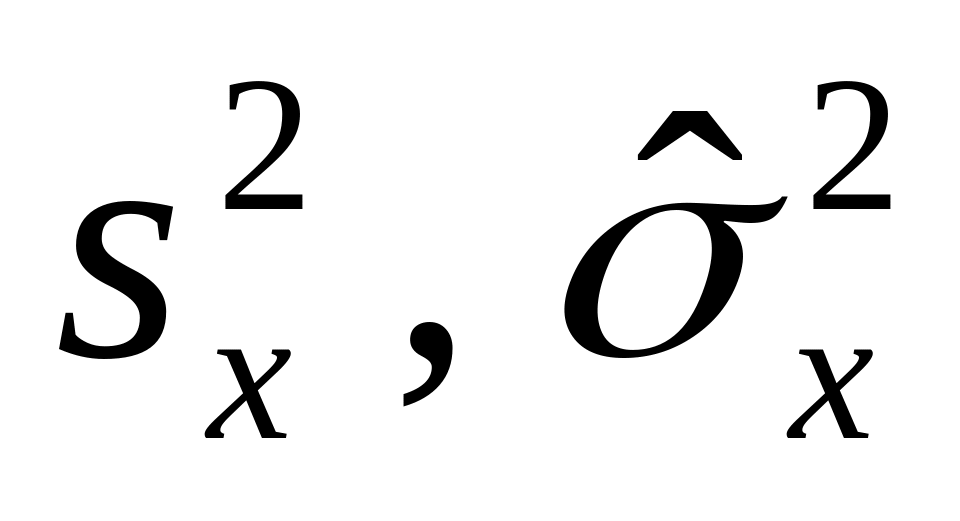– выборочные оценки дисперсии; 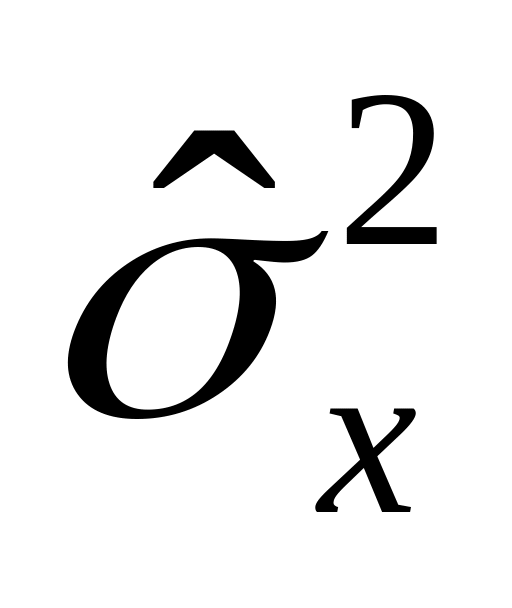– несмещенная оценка (исправленная на ЧСС)
   f (x) – дифференциальная функция распределения, плотность вероятности	Гистограмма – ступенчатый график плотности вероятности 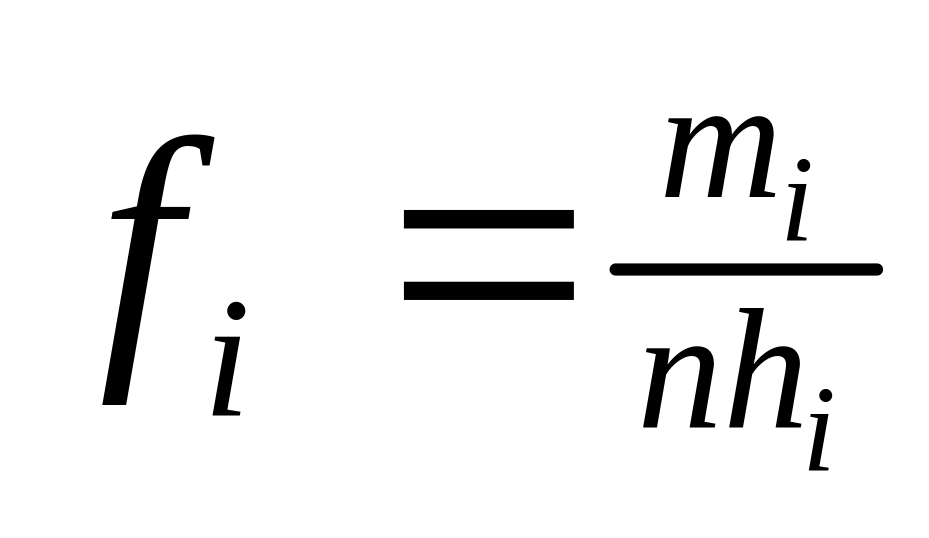, где hi – ширина интервала
   F(x) – функция распределения (интегральная функция распределения) F(x) = Р(Х  х)	Кумулята – график накопленных относительных частот

2. Записати порівняльні формули для обчислення характеристик і їх вибіркових оцінок: математичного сподівання, дисперсії, коваріації.

Генеральная совокупность	Выборочные оценки
М(х) =  xipi – для дискретной случайной величины; – для непрерывной случайной величины	– для несгруппированных данных; – для данных, сгруппированных на k интервалов (mj – частоты, mj – центры интервалов)
; .
; .

3. Пояснити, що означає “спроможність”, “незміщеність” і “ефективність” статистичних оцінок. Привести формулу для обчислення незміщеної оцінки дисперсії.

Оценка b параметра  называется состоятельной, если при увеличении объема выборки (n  ) оценка стремится к своему генеральному значению b   . Оценка называется несмещенной, если М(b) =  , т.е. отдельные значения оценок по разным выборкам группируются вокруг генерального значения  ; несмещенная оценка не имеет систематической ошибки. Оценка называется эффективной, если по сравнению с другими оценками она имеет наименьшую дисперсию (эффективная оценка имеет наименьшую погрешность). Оценка дисперсии систематически занижена. Несмещенная оценка (исправленная на ЧСС – число степеней свободы) несколько больше: , где ЧСС равно разности между числом случайных величин и числом наложенных на них линейных связей. Обычно ЧСС = n – 1.

4. Перелічити властивості математичного сподівання і вибіркового середнього, привести приклади їх використання (сформулювати “нульову властивість” математичного сподівання, спростити формули для обчислення дисперсії і коваріації, обґрунтувати можливість застосування умовних змінних).

Свойства: М(а) = а; М(kx) = kM(x); M(x+y) = M(x) + M(y); M(xy) = M(x)M(y).

для независимых х, у.

Следствия: Если а = М(х), то М(х – а) = 0 – «нулевое свойство»; аналогично:

; .

. .

Для независимых х, у ковариация _xy (s_xy) равна нулю.

Условная переменная: ; Обратно: x = c + hX; Тогда .

5. Перелічити властивості дисперсії. Записати формули для обчислення дисперсії суми і дисперсії різниці випадкових величин (залежних і незалежних). Сформулювати правило “3-х сигм”. Пояснити, що таке “коефіцієнт варіації” і в яких ситуаціях він використовується.

Свойства: D(а) = 0; D(kx) = k²D(x); D(x+y) = D(x) + D(y) + 2Cov(x, y).

Следствия: D(x+y) = ²D(x) + ²D(y) + 2Cov(x, y).

Для независимых х, у: D(x+y) = ²D(x) + ²D(y) ; D(xy) = D(x) + D(y) .

Условная переменная: ; Обратно: x = c + hX; Тогда s_x = hs_X.

Правило 3-х сигм: С уровнем доверия, не меньшим 90% , можно утверждать, что случайные отклонения от центра не превышают 3-х стандартных (среднеквадратичных) отклонений.: P(|x – a|  3_x) > 0,89 , где a = М(x). Это правило имеет место для любых случайных величин, независимо от вида их распределения.

Если коэффициент вариации меньше 2% , случайной изменчивостью можно пренебречь.