
- •Cортировка массива методом Хоара(«Быстрая» сортировка) – сравнение параллельной и последовательной реализации
- •Описание «быстрой» сортировки
- •Алгоритм сортировки
- •Cортировка массива методом Хоара(«Быстрая» сортировка) – сравнение параллельной и последовательной реализации
- •Описание «быстрой» сортировки
- •Алгоритм сортировки
Алгоритм 6. Быстрая сортировка
Теперь переходим к самому интересному, а именно к одной из самых быстрых и эффективных из известных сортировок, которая так и называется — «быстрая сортировка».
Как и в сортировке слиянием, массив разбивается на две части, с условием, что все элементы первой части меньше любого элемента второй. Потом каждая часть сортируется отдельно. Разбиение на части достигается упорядочиванием относительно некоторого элемента массива, т. е. в первой части все числа меньше либо равны этому элементу, а во второй, соответственно, больше либо равны. Два индекса проходят по массиву с разных сторон и ищут элементы, которые попали не в свою группу. Найдя такие элементы, их меняют местами. Тот элемент, на котором индексы пересекутся, и определяет разбиение на группы.
Что же делает данный алгоритм таким быстрым? Ну во-первых, если массив каждый раз будет делится на приблизительно равные части, то для него будет верно то же соотношение, что и для сортировки слиянием, т. е. время работы будет O(nlog2n). Это уже само по себе хорошо. Кроме того, константа при nlog2n очень мала, ввиду простоты внутреннего цикла программы. В комплексе это обеспечивает огромную скорость работы. Но как всегда есть одно «но». Вы, наверное, уже задумались: а что если массив не будет делится на равные части? Классическим примером является попытка «быстро» отсортировать уже отсортированный массив. При этом данные каждый раз будут делиться в пропорции 1 к n-1, и так n раз. Общее время работы при этом будет O(n2), тогда как вставкам, для того чтобы «понять», что массив уже отсортирован, требуется всего-навсего O(n). А на кой нам сортировка, которая одно сортирует хорошо, а другое плохо? А собственно, что она сортирует хорошо? Оказывается, что лучше всего она сортирует случайные массивы (порядок элементов в массиве случаен). И поэтому нам предлагают ввести в алгоритм долю случайности. А точнее, вставить randomize и вместо r:=A[p]; написать r:=A[random(q-p)+p]; т. е. теперь мы разбиваем данные не относительно конкретного, а относительно случайного элемента. Благодаря этому алгоритм получает приставку к имени «вероятностный». Особо недоверчивым предлагаю на своем опыте убедится, что данная модификация быстрой сортировки сортирует любые массивы столь же быстро.
А теперь еще один интересный факт: время O(nlog2n) является минимальным для сортировок, которые используют только попарное сравнение элементов и не использует структуру самих элементов. Тем, кому интересно, откуда это взялось, рекомендую поискать в литературе, доказательство я здесь приводить не намерен, не Дональд Кнут, в конце концов :-). Но вы обратили внимание, что для рассмотренных алгоритмов в принципе не важно, что сортировать — такими методами можно сортировать хоть числа, хоть строки, хоть какие-то абстрактные объекты. Следующие сортировки могут сортировать только определенные типы данных, но за счет этого они имеют рекордную временную оценку O(n).
Основа алгоритма была разработана в 1960 году (C.A.R.Hoare) и с тех пор внимательно изучалась многими людьми. Быстрая сортировка особенно популярна ввиду легкости ее реализации; это довольно хороший алгоритм общего назначения, который хорошо работает во многих ситуациях, и использует при этом меньше ресурсов, чем другие алгоритмы.
Основные достоинства этого алгоритма состоят в том, что он точечный (использует лишь небольшой дополнительный стек), в среднем требует только около N log N операций для того, чтобы отсортировать N элементов, и имеет экстремально короткий внутренний цикл. Недостатки алгоритма состоят в том, что он рекурсивен (реализация очень затруднена когда рекурсия недоступна), в худшем случае он требует N2 операций, кроме того он очень "хрупок": небольшая ошибка в реализации, которая легко может пройти незамеченной, может привести к тому, что алгоритм будет работать очень плохо на некоторых файлах.
Производительность быстрой сортировки хорошо изучена. Алгоритм подвергался математическому анализу, поэтому существуют точные математические формулы касающиеся вопросов его производительности. Результаты анализа были неоднократно проверены эмпирическим путем, и алгоритм был отработан до такого состояния, что стал наиболее предпочтительным для широкого спектра задач сортировки. Все это делает алгоритм стоящим более детального изучения наиболее эффективных путей его реализации. Похожие способы реализации подходят также и для других алгоритмов, но в алгоритме быстрой сортировки мы можем использовать их с уверенностью, поскольку его производительность хорошо изучена.
Улучшить алгоритм быстрой сортировки является большим искушением: более быстрый алгоритм сортировки - это своеобразная "мышеловка" для программистов. Почти с того момента, как Oia?a впервые опубликовал свой алгоритм, в литературе стали появляться "улучшенные" версии этого алгоритма. Было опробовано и проанализировано множество идей, но все равно очень просто обмануться, поскольку алгоритм настолько хорошо сбалансирован, что результатом улучшения в одной его части может стать более сильное ухудшение в другой его части. Мы изучим в некоторых деталях три модификации этого алгоритма, которые дают ему существенное улучшение.
Хорошо же отлаженная версия быстрой сортировки скорее всего будет работать гораздо быстрее, чем любой другой алгоритм. Однако стоит еще раз напомнить, что алгоритм очень хрупок и любое его изменение может привести к нежелательным и неожиданным эффектам для некоторых входных данных.
Суть алгоритма: число операций перемены местоположений элементов внутри массива значительно сократится, если менять местами далеко стоящие друг от друга элементы. Для этого выбирается для сравнения один элемент х, отыскивается слева первый элемент, который не меньше х, а справа первый элемент, который не больше х. Найденные элементы меняются местами. После первого же прохода все элементы, которые меньше х, будут стоять слева от х, а все элементы, которые больше х, - справа от х. С двумя половинами массива поступают точно также. Продолжая деление этих половин до тех пор пока не останется в них по 1 элементу.
program Quitsort; uses crt; Const N=10; Type Mas=array[1..n] of integer; var a: mas; k: integer; function Part(l, r: integer):integer; var v, i, j, b: integer; begin V:=a[r];I:=l-1 j:=r; repeat repeat dec(j) until (a[j]<=v) or (j=i+1); repeat inc(i) until (a[i]>=v) or (i=j-1); b:=a[i]; a[i]:=a[j]; a[j]:=b; until i>=j; a[j]:=a[i]; a[i]:= a[r]; a[r]:=b; part:=i; end; procedure QuickSort(l, t: integer); var i: integer; begin if l<t then begin i:=part(l, t); QuickSort(l,i-1); QuickSort(i+1,t); end; end; begin clrscr; randomize; for k:=1 to 10 do begin a[k]:=random(100); write(a[k]:3); end; QuickSort(1,n); writeln; for k:=1 to n do write(a[k]:3); readln; end.
Пример: 60,79, 82, 58, 39, 9, 54, 92, 44, 32 60,79, 82, 58, 39, 9, 54, 92, 44, 32 9,79, 82, 58, 39, 60, 54, 92, 44, 32 9,79, 82, 58, 39, 60, 54, 92, 44, 32 9, 32, 82, 58, 39, 60, 54, 92, 44, 79 9, 32, 44, 58, 39, 60, 54, 92, 82, 79 9, 32, 44, 58, 39, 54, 60, 92, 82, 79 9, 32, 44, 58, 39, 92, 60, 54, 82, 79 9, 32, 44, 58, 39, 54, 60, 79, 82, 92 9, 32, 44, 58, 54, 39, 60, 79, 82, 92 9, 32, 44, 58, 60, 39, 54, 79, 82, 92 9, 32, 44, 58, 54, 39, 60, 79, 82, 92 9, 32, 44, 58, 54, 39, 60, 79, 82, 92 9, 32, 44, 58, 54, 39, 60, 79, 82, 92 9, 32, 39, 58, 54, 44, 60, 79, 82, 92 9, 32, 39, 58, 54, 44, 60, 79, 82, 92 9, 32, 39, 44, 54, 58, 60, 79, 82, 92 9, 32, 39, 44, 58, 54, 60, 79, 82, 92 9, 32, 39, 44, 54, 58, 60, 79, 82, 92 9, 32, 39, 44, 54, 58, 60, 79, 92, 82 9, 32, 39, 44, 54, 58, 60, 79, 82, 92
"Внутренний цикл" быстрой сортировки состоит только из увеличения указателя и сравнения элементов массива с фиксированным числом. Это как раз и делает быструю сортировку быстрой. Сложно придумать более простой внутренний цикл. Положительные эффекты сторожевых ключей также оказывают здесь свое влияние, поскольку добавление еще одной проверки к внутреннему циклу оказало бы отрицательное влияние на производительность алгоритма.
Самая сомнительная черта вышеприведенной программы состоит в том, что она очень мало эффективна на простых подфайлах. Например, если файл уже сортирован, то разделы будут вырожденными, и программа просто вызовет сама себя N раз, каждый раз с меньшим на один элемент подфайлом. Это означает, что не только производительность программы упадет примерно до N2/2, но и пространство необходимое для ее работы будет около N (смотри ниже), что неприемлемо. К счастью, есть довольно простые способы сделать так, чтобы такой "худший" случай не произошел при практическом использовании программы.
Когда в файле присутствуют одинаковые ключи, то возникает еще два сомнительных вопроса. Первое, должны ли оба указателя останавливаться на ключах равных делящему элементу или останавливать только один из них, а второй будет проходить их все, или оба указателя должны проходить над ними. На самом деле, этот вопрос детально изучался, и результаты показали, что самое лучшее - это останавливать оба указателя. Это позволяет удерживать более или менее сбалансированные разделы в присутствии многих одинаковых ключей. На самом деле, эта программа может быть слегка улучшена терминированием сканирования j<i, и использованием после этого quicksort(l, j) для первого рекурсивного вызова.
Характеристики Производительности Быстрой Сортировки
Самое лучшее, что могло бы произойти для алгоритма - это если бы каждый из подфайлов делился бы на два равных по величине подфайла. В результате количество сравнений делаемых быстрой сортировкой было бы равно значению рекурсивного выражения
CN = 2CN/2+N - наилучший случай.
(2CN/2 покрывает расходы по сортировке двух полученных подфайлов; N - это стоимость обработки каждого элемента, используя один или другой указатель.) Нам известно также, что примерное значение этого выражения равно CN = N lg N.
Хотя мы встречаемся с подобной ситуацией не так часто, но в среднем время работы программы будет соответствовать этой формуле. Если принять во внимание вероятные позиции каждого раздела, то это сделает вычисления более сложными, но конечный результат будет аналогичным.
Свойство 1 Быстрая сортировка в среднем использует 2N ln N сравнений.
Методы улучшения быстрой сортировки.
1. Небольшие Подфайлы.
Первое улучшение в алгоритме быстрой сортировки возникает из наблюдения, что программа гарантировано вызывает себя для огромного количества небольших подфайлов, поэтому следует использовать самый лучший метод сортировки когда мы встречаем небольшой подфайл. Очевидный способ добиться этого, это изменить проверку в начале рекурсивной функции из "if r>l then" на вызов сортировки вставкой (соответственно измененной для восприятия границ сортируемого подфайла): "if r-l<=M then insertion(l, r)." Значение для M не обязано быть "самым-самым" лучшим: алгоритм работает примерно одинаково для M от 5 до 25. Время работы программы при этом снижается примерно на 20% для большинства программ.
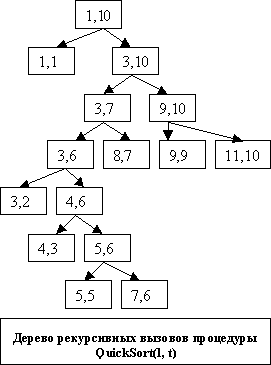
При небольших подфайлах (5- 25 элементов) быстрая сортировка очень много раз вызывает сама себя (в наше примере для 10 элементов она вызвала сама себя 15 раз), поэтому следует применять не быструю сортировку, а сортировку вставкой.
procedure QuickSort (l,t:integer); var i:integer; begin if t-l>m then begin i:=part(l,t); QuickSort (l,i-1); QuickSort (i+1,t); end Else Insert(l,t); end;
2. Деление по Медиане из Трех
Второе улучшение в алгоритме быстрой сортировки состоит в попытке использования лучшего делящего элемента. У нас есть несколько возможностей. Наиболее безопасная из них будет попытка избежать худшего случая посредством выбора произвольного элемента массива в качестве делящего элемента. Тогда вероятность худшего случая становится пренебрежимо мала. Это простой пример "вероятностного" алгоритма, который почти всегда работает вне зависимости от входных данных. Произвольность может быть хорошим инструментом при разработке алгоритмов, особенно если возможны подозрительные входные данные.
Более полезное улучшение состоит в том, чтобы взять из файла три элемента, и затем использовать среднее из них в качестве делящего элемента. Если элементы взяты из начала, середины, и конца файла, то можно избежать использования сторожевых элементов: сортируем взятые три элемента, затем обмениваем центральный элемент с a[r-1], и затем используем алгоритм деления на массиве a[l+1..r-2]. Это улучшение называется делением по медиане из трех.
Метод деления по медиане из трех полезен по трем причинам. Во-первых, он делает вероятность худшего случая гораздо более низкой. Чтобы этот алгоритм использовал время пропорциональной N2, два из трех взятых элементов должны быть либо самыми меньшими, либо самыми большими, и это должно повторяться из раздела в раздел. Во-вторых, этот метод уничтожает необходимость в сторожевых элементах, поскольку эту роль играет один из трех взятых нами перед делением элементов. В третьих, он на самом деле снижает время работы алгоритма приблизительно на 5%.
procedure exchange(i,j:integer); var k:integer; begin k:=a[i]; a[i]:=a[j]; a[j]:=k; end; procedure Mediana; var i:integer; begin i:=n div 4;{Рис.} if a[i]>a[i*2] then if a[i]>a[i*3] then exchange(i,n) else exchange(i*3,n) else if a[i*2]>a[i*3] then exchange(i*2,n); quicksort(1,n); end;
3. Нерекурсивная реализация.
Можно переписать данный алгоритм без использования рекурсии используя стек, но здесь мы это не будем делать.
Комбинация нерекурсивной реализации деления по медиане из трех с отсечением на небольшие файлы может улучшить время работы алгоритма от 25% до 30%.
1. Небольшие Подфайлы.
Первое улучшение в алгоритме быстрой сортировки возникает из наблюдения, что программа гарантировано вызывает себя для огромного количества небольших подфайлов, поэтому следует использовать самый лучший метод сортировки когда мы встречаем небольшой подфайл. Очевидный способ добиться этого, это изменить проверку в начале рекурсивной функции из "if r>l then" на вызов сортировки вставкой (соответственно измененной для восприятия границ сортируемого подфайла): "if r-l<=M then insertion(l, r)." Значение для M не обязано быть "самым-самым" лучшим: алгоритм работает примерно одинаково для M от 5 до 25. Время работы программы при этом снижается примерно на 20% для большинства программ.
При небольших подфайлах (5- 25 элементов) быстрая сортировка очень много раз вызывает сама себя (в наше примере для 10 элементов она вызвала сама себя 15 раз), поэтому следует применять не быструю сортировку, а сортировку вставкой.
procedure QuickSort (l,t:integer);
var
i:integer;
begin
if t-l>m then
begin
i:=part(l,t);
QuickSort (l,i-1);
QuickSort (i+1,t);
end
Else
Insert(l,t);
end;
2. Деление по Медиане из Трех
Второе улучшение в алгоритме быстрой сортировки состоит в попытке использования лучшего делящего элемента. У нас есть несколько возможностей. Наиболее безопасная из них будет попытка избежать худшего случая посредством выбора произвольного элемента массива в качестве делящего элемента. Тогда вероятность худшего случая становится пренебрежимо мала. Это простой пример "вероятностного" алгоритма, который почти всегда работает вне зависимости от входных данных. Произвольность может быть хорошим инструментом при разработке алгоритмов, особенно если возможны подозрительные входные данные.
Более полезное улучшение состоит в том, чтобы взять из файла три элемента, и затем использовать среднее из них в качестве делящего элемента. Если элементы взяты из начала, середины, и конца файла, то можно избежать использования сторожевых элементов: сортируем взятые три элемента, затем обмениваем центральный элемент с a[r-1], и затем используем алгоритм деления на массиве a[l+1..r-2]. Это улучшение называется делением по медиане из трех.
Метод деления по медиане из трех полезен по трем причинам. Во-первых, он делает вероятность худшего случая гораздо более низкой. Чтобы этот алгоритм использовал время пропорциональной N2, два из трех взятых элементов должны быть либо самыми меньшими, либо самыми большими, и это должно повторяться из раздела в раздел. Во-вторых, этот метод уничтожает необходимость в сторожевых элементах, поскольку эту роль играет один из трех взятых нами перед делением элементов. В третьих, он на самом деле снижает время работы алгоритма приблизительно на 5%.
procedure exchange(i,j:integer);
var
k:integer;
begin
k:=a[i];
a[i]:=a[j];
a[j]:=k;
end;
procedure Mediana;
var i:integer;
begin
i:=n div 4;{Рис.}
if a[i]>a[i*2] then
if a[i]>a[i*3] then
exchange(i,n)
else
exchange(i*3,n)
else
if a[i*2]>a[i*3] then
exchange(i*2,n);
quicksort(1,n);
end;
Некоторые из представленных здесь реализаций используют в качестве опорного элемента один из крайних элементов подмассива. Эти реализации страдают одним общим недостатком: при передаче им уже отсортированного массива в качестве параметра, их время работы становится порядка Θ(n2).
В качестве опорного элемента следует выбирать случайный элемент массива, чтобы получить гарантированное время сортировкиΘ(nlogn) в среднем. В случае, если использование случайных чисел нежелательно, в качестве опорного элемента можно выбрать, например, элемент в середине массива, но такие алгоритмы всё равно будут работать за Θ(n2) времени на некоторых специально-сконструированных массивах.
C
Работает для произвольного массива из n целых чисел.
int n, a[n]; //n - количество элементов
void qs(int* s_arr,int first, int last)
{
int i = first, j = last, x = s_arr[(first + last) / 2];
do {
while (s_arr[i] < x) i++;
while (s_arr[j] > x) j--;
if(i <= j) {
if (i < j) swap(s_arr + i, s_arr + j);
i++;
j--;
}
} while (i <= j);
if (i < last)
qs(s_arr, i, last);
if (first < j)
qs(s_arr, first,j);
}
Исходный вызов функции qs для массива из n элементов будет иметь следующий вид.
qs(a, 0, n-1);
Java/C#
int partition (int[] array, int start, int end) {
int marker = srart;
for ( int i = start; i <= end; i++ ) {
if ( array[i] <= array[end] ) {
int temp = array[marker];
array[marker] = array[i];
array[i] = temp;
marker += 1;
}
}
return marker - 1;
}
void quicksort (int[] array, int start, int end) {
int pivot;
if ( start >= end ) {
return;
}
pivot = partition (array, start, end);
quicksort (array, start, pivot-1);
quicksort (array, pivot+1, end);
}
C# с обобщенными типами, тип Т должен реализовывать интерфейс IComparable<T>
int partition<T>( T[] m, int a, int b) where T :IComparable<T>
{
int i = a;
for (int j = a; j <= b; j++) // просматриваем с a по b
{
if (m[j].CompareTo( m[b]) <= 0) // если элемент m[j] не превосходит m[b],
{
T t = m[i]; // меняем местами m[j] и m[a], m[a+1], m[a+2] и так далее...
m[i] = m[j]; // то есть переносим элементы меньшие m[b] в начало,
m[j] = t; // а затем и сам m[b] «сверху»
i++; // таким образом последний обмен: m[b] и m[i], после чего i++
}
}
return i - 1; // в индексе i хранится <новая позиция элемента m[b]> + 1
}
void quicksort<T>( T[] m, int a, int b) where T : IComparable<T>// a - начало подмножества, b - конец
{ // для первого вызова: a = 0, b = <элементов в массиве> - 1
if (a >= b) return;
int c = partition( m, a, b);
quicksort( m, a, c - 1);
quicksort( m, c + 1, b);
}
//Пример вызова
//double[] arr = {9,1.5,34.4,234,1,56.5};
//quicksort<double>(arr,0,arr.Length-1);
//
C# с использованием лямбда-выражений
using System;
using System.Collections.Generic;
using System.Linq;
static public class Qsort
{
public static IEnumerable<T> QuickSort<T>(this IEnumerable<T> list) where T : IComparable<T>
{
if (!list.Any())
{
return Enumerable.Empty<T>();
}
var pivot = list.First();
var smaller = list.Skip(1).Where(item => item.CompareTo(pivot) <= 0).QuickSort();
var larger = list.Skip(1).Where(item => item.CompareTo(pivot) > 0).QuickSort();
return smaller.Concat(new[] { pivot }).Concat(larger);
}
//(тоже самое, но записанное в одну строку, без объявления переменных)
public static IEnumerable<T> shortQuickSort<T>(this IEnumerable<T> list) where T : IComparable<T>
{
return !list.Any() ? Enumerable.Empty<T>() : list.Skip(1).Where(
item => item.CompareTo(list.First()) <= 0).shortQuickSort().Concat(new[] { list.First() })
.Concat(list.Skip(1).Where(item => item.CompareTo(list.First()) > 0).shortQuickSort());
}
}
JavaScript
/*
* Алгоритм быстрой сортировки
*
* @param data Array
* @param compare function(a, b) - возвращает 0 если a=b, -1 если a<b и 1 если a>b (необязательная)
* @param change function(a, i, j) - меняет местами i-й и j-й элементы массива а (необязательная)
*
*/
function qsort(data, compare, change) {
var a = data,
f_compare = compare,
f_change = change;
if (!a instanceof Array) { // Данные не являются массивом
return undefined;
};
if (f_compare == undefined) { // Будем использовать простую функцию (для чисел)
f_compare = function(a, b) {return ((a == b) ? 0 : ((a > b) ? 1 : -1));};
};
if (f_change == undefined) { // Будем использовать простую смены (для чисел)
f_change = function(a, i, j) {var c = a[i];a[i] = a[j];a[j] = c;};
};
var qs = function (l, r) {
var i = l,
j = r,
x = a[Math.floor(Math.random()*(r-l+1))+l];
// x = a[l]; // Если нет желания использовать объект Math
while(i <= j) {
while(f_compare(a[i], x) == -1) {i++;}
while(f_compare(a[j], x) == 1) {j--;}
if(i <= j) {f_change(a, i++, j--);}
};
if(l < j) {qs(l, j);}
if(i < r) {qs(i, r);}
};
qs(0, a.length-1);
};
Ruby
Вариант 1:
class Array
def qsort
return self.dup if size <=1
l,r = partition {|x| x <= self.first}
c,l = l.partition {|x| x == self.first}
l.qsort + с + r.qsort
end
end
Вариант 2:
class Array
def partition3
a = Array.new(3) {|i| []}
each do |x|
a[yield(x)].push x
end
a
end
def qsort
return self.dup if size <=1
c,l,r = partition3 {|x| first <=> x}
l.qsort + c + r.qsort
end
end
Python
def qsort(L):
if L == []: return []
return qsort([x for x in L[1:] if x< L[0]]) + L[0:1] + qsort([x for x in L[1:] if x>=L[0]])
Haskell
qsort [] = []
qsort (x:xs) = qsort (filter (< x) xs) ++ [x] ++ qsort (filter (>= x) xs)
Pascal
В данном примере показан наиболее полный вид алгоритма, очищенный от особенностей, обусловленных применяемым языком. В комментариях показано несколько вариантов. Представленный вариант алгоритма выбирает опорный элемент псевдослучайным образом, что, теоретически, сводит вероятность возникновения самого худшего или приближающегося к нему случая к минимуму. Недостаток его — зависимость скорости алгоритма от реализации генератора псевдослучайных чисел. Если генератор работает медленно или выдаёт плохие последовательности ПСЧ, возможно замедление работы. В комментарии приведён вариант выбора среднего значения в массиве — он проще и быстрее, хотя, теоретически, может быть хуже.
Внутреннее условие, помеченное комментарием «это условие можно убрать» — необязательно. Его наличие влияет на действия в ситуации, когда поиск находит два равных ключа: при наличии проверки они останутся на местах, а при отсутствии — будут обменены местами. Что займёт больше времени — проверки или лишние перестановки, — зависит как от архитектуры, так и от содержимого массива (очевидно, что при наличии большого количества равных элементов лишних перестановок станет больше). Следует особо отметить, что наличие условия не делает данный метод сортировки устойчивым.
const max=20; { можно и больше... }
type
list = array[1..max] of integer;
procedure quicksort(var a: list; Lo,Hi: integer);
procedure sort(l,r: integer);
var
i,j,x,y: integer;
begin
i:=l; j:=r; x:=a[random(r-l+1)+l]; { x := a[(r+l) div 2]; - для выбора среднего элемента }
repeat
while a[i]<x do i:=i+1; { a[i] > x - сортировка по убыванию}
while x<a[j] do j:=j-1; { x > a[j] - сортировка по убыванию}
if i<=j then
begin
if a[i] > a[j] then {это условие можно убрать} {a[i] < a[j] при сортировке по убыванию}
begin
y:=a[i]; a[i]:=a[j]; a[j]:=y;
end;
i:=i+1; j:=j-1;
end;
until i>=j;
if l<j then sort(l,j);
if i<r then sort(i,r);
end; {sort}
begin {quicksort};
randomize; {нужно только если используется выборка случайного опорного элемента}
sort(Lo,Hi)
end; {quicksort}
Устойчивый вариант (требует дополнительно O(n)памяти)
const max=20; { можно и больше… }
type
list = array[1..max] of integer;
procedure quicksort(var a: list; Lo,Hi: integer);
procedure sort(l,r: integer);
var
i,j,x,xval,y: integer;
begin
i:=l; j:=r; x:=random(r-l+1)+l; xval:=a[x]; xvaln:=num[x]{ x :=(r+l) div 2; - для выбора среднего элемента }
repeat
while (a[i]<xval)or((a[i]=xval)and(num[i]<xvaln)) do i:=i+1; {> - сортировка по убыванию}
while (xval<a[j])or((a[j]=xval)and(xvaln<num[j])) do j:=j-1; {> - сортировка по убыванию}
if i<=j then
begin
y:=a[i]; a[i]:=a[j]; a[j]:=y;
y:=num[i]; num[i]:=num[j]; num[j]:=y;
i:=i+1; j:=j-1
end;
until i>j;
if l<j then sort(l,j);
if i<r then sort(i,r)
end; {sort}
begin {quicksort}
randomize; {нужно только если используется выборка случайного опорного элемента}
for i:=1 to n do
num[i]:=i;
sort(Lo,Hi)
end; {quicksort}
Быстрая сортировка, нерекурсивный вариант
Нерекурсивная реализация быстрой сортировки через стек. Функции compare и change реализуются в зависимости от типа данных.
procedure quickSort(var X: itemArray; n: integer);
type
p_node = ^node;
node = record
node: integer;
next: p_node
end;
var
l,r,i,j: integer;
stack: p_node;
temp: item;
procedure push(i: integer);
var
temp: p_node;
begin
new(temp);
temp^.node:=i;
temp^.next:=stack;
stack:=temp
end;
function pop: integer;
var
temp: p_node;
begin
if stack=nil then
pop:=0
else
begin
temp:=stack;
pop:=stack^.node;
stack:=stack^.next;
dispose(temp)
end
end;
begin
stack:=nil;
push(n-1);
push(0);
repeat
l:=pop;
r:=pop;
if r-l=1 then
begin
if compare(X[l],X[r]) then
change(X[l],X[r])
end
else
begin
temp:=x[(l+r) div 2]; {random(r-l+1)+l}
i:=l;
j:=r;
repeat
while compare(temp,X[i]) do i:=i+1;
while compare(X[j],temp) do j:=j-1;
if i<=j then
begin
change(X[i],X[j]);
i:=i+1;
j:=j-1
end;
until i>j;
if l<j then
begin
push(j);
push(l)
end;
if i<r then
begin
push(r);
push(i)
end
end;
until stack=nil
end;
Prolog
split(H, [A|X], [A|Y], Z) :-
order(A, H), split(H, X, Y, Z).
split(H, [A|X], Y, [A|Z]) :-
not(order(A, H)), split(H, X, Y, Z).
split(_, [], [], []).
quicksort([], X, X).
quicksort([H|T], S, X) :-
split(H, T, A, B),
quicksort(A, S, [H|Y]),
quicksort(B, Y, X).
Perl
#! /usr/bin/perl
use strict;
sub qsort {
my ($q, $s, $e) = @_;
my $m = $s-1;
for (my $i = $s; $i < $e; $i++) {
if ($q->[$i] < $q->[$e]) {
$m++;
($q->[$m], $q->[$i]) = ($q->[$i], $q->[$m]);
}
}
$m++;
($q->[$m], $q->[$e]) = ($q->[$e], $q->[$m]);
qsort($q, $s, $m-1) if $s < $m-1;
qsort($q, $m+1, $e) if $m+1 < $e;
}
my @data = map { int(rand(10)) } (1 .. 30);
print "@data\n";
qsort(\@data, 0, $#data);
print "@data\n";
F#
let rec quicksort = function
[] -> []
| h::t -> quicksort ([ for x in t when x<=h -> x])
@ [h] @ quicksort ([ for x in t when x>h -> x]);;
OCaml
let rec qsort l=match l with
[]->[]
|a::b-> (qsort (List.filter ((>=) a) b) lt) @ [a] @ (qsort (List.filter ((<) a) b ));;
Erlang
qsort([]) -> [];
qsort([H|T]) -> qsort([X || X <- T, X < H]) ++ [H] ++ qsort([X || X <- T, X >= H])].
D
array qsort(array)(array _a)
{
alias typeof(array.init[0]) _type;
array filter(bool delegate(_type) dg, array a){
array buffer = null;
foreach(value; a) {
if(dg(value)){
buffer ~= value;
}
}
return buffer;
}
if(_a.length <= 1) {
return _a;
}
else {
return qsort( filter((_type e){ return _a[0] >= e; }, _a[1 .. $] ) ) ~ _a[0] ~
qsort( filter((_type e){ return _a[0] < e; }, _a[1 .. $] ) );
}
}
Scala
def qsort[A <% Ordered[A]](list: List[A]): List[A] = list match
{
case head::tail =>
{
qsort( tail filter(head>=) ) ::: head :: qsort( tail filter(head<) )
}
case _ => list;
}
PHP
function quicksort (&$array, $l, $r) {
function swap (&$x, &$y) {
list($x, $y) = array($y, $x);
}
function qsort ($left, $right) {
global $array;
$i = $left;
$j = $right;
$x = $array[($left + $right) / 2];
do {
while ($array[$i] < $x) $i++;
while ($array[$j] > $x) $j--;
if ($i <= $j) {
if ($array[$i] > $array[$j]) swap ($array[$i], $array[$j]);
$i++;
$j--;
}
} while ($i <= $j);
if ($i < $right) qsort ($i, $right);
if ($j > $left) qsort ($left, $j);
}
qsort ($l, $r);
}
Встроенный язык 1С
Здесь приведен алгоритм сортировки на примере объекта типа "СписокЗначений", но его можно модифицировать для работы с любым объектом, для этого нужно изменить соответствующим образом код функций "СравнитьЗначения", "ПолучитьЗначение", "УстановитьЗначение".
Функция СравнитьЗначения(Знач1, Знач2)
Если Знач1>Знач2 Тогда
Возврат 1;
КонецЕсли;
Если Знач1<Знач2 Тогда
Возврат -1;
КонецЕсли;
Возврат 0;
КонецФункции
Функция ПолучитьЗначение(Список, Номер)
стр="";
Возврат Список.ПолучитьЗначение(Номер, стр);
КонецФункции
Процедура УстановитьЗначение(Список, Номер, Значение)
Список.УстановитьЗначение(Номер, Значение);
КонецПроцедуры
Процедура qs_0(s_arr, first, last)
i = first;
j = last;
x = ПолучитьЗначение(s_arr, (first + last) / 2);
Пока СравнитьЗначения(ПолучитьЗначение(s_arr, i), x)=-1 Цикл
i=i+1;
КонецЦикла;
Пока СравнитьЗначения(ПолучитьЗначение(s_arr, j), x)=1 Цикл
j=j-1;
КонецЦикла;
Если i <= j Тогда
Если i < j Тогда
к=ПолучитьЗначение(s_arr, i);
УстановитьЗначение(s_arr, i, ПолучитьЗначение(s_arr, j));
УстановитьЗначение(s_arr, j, к);
КонецЕсли;
i=i+1;
j=j-1;
КонецЕсли;
Пока i <= j Цикл
Пока СравнитьЗначения(ПолучитьЗначение(s_arr, i), x)=-1 Цикл
i=i+1;
КонецЦикла;
Пока СравнитьЗначения(ПолучитьЗначение(s_arr, j), x)=1 Цикл
j=j-1;
КонецЦикла;
Если i <= j Тогда
Если i < j Тогда
к=ПолучитьЗначение(s_arr, i);
УстановитьЗначение(s_arr, i, ПолучитьЗначение(s_arr, j));
УстановитьЗначение(s_arr, j, к);
КонецЕсли;
i=i+1;
j=j-1;
КонецЕсли;
КонецЦикла;
Если i < last Тогда
qs_0(s_arr, i, last);
КонецЕсли;
Если first < j Тогда
qs_0(s_arr, first,j);
КонецЕсли;
КонецПроцедуры
Процедура Сортировать(Список, Размер="", Первый="", Последний="")
Если ПустоеЗначение(Первый)=1 Тогда
Первый=1;
КонецЕсли;
Если ПустоеЗначение(Последний)=1 Тогда
Последний=Размер;
КонецЕсли;
qs_0(Список, Первый, Последний);
КонецПроцедуры
Cортировка массива методом Хоара(«Быстрая» сортировка) – сравнение параллельной и последовательной реализации
01.10.2011
Как и для большинства алгоритмов сортировки, методика «быстрой» сортировки взята из повседневного опыта. Чтобы отсортировать большую стопку алфавитных карточек по именам, можно разбить ее на две меньшие стопки относительно какой-нибудь буквы, например K. Все имена, меньшие или равные K, идут в одну стопку, а остальные – в другую.
Данный алгоритм очень удачно подходит для распараллеливания. Меня заинтересовало, какой прирост к производительности будет, если использовать потоки.
Описание «быстрой» сортировки
Подробно о самой сортировке можно прочитать на том же rsdn. Тут коснусь пары основных моментов. Вообще, главное в данной сортировке, что после выбора опорного элемента, слева от него остаются все элементы меньше его, а справа большие. И далее происходит рекурсивный вызов функции сортировки для каждого подмассива. Идея в том, чтобы сортировку обеих частей провести в отдельных поток. Теоретически, в идеальном варианте, когда слева и справа одинаковое число элементов, создавая 2 потока на 2-х ядерном процессоре, скорость выполнения должна увеличиться на 100%.
Алгоритм сортировки
Реализация сортировки наивная, опорным элементом изначально всегда берётся серединный элемент массива. При ветвлении создание потоков для обеих веток не разумно, ибо затраты на создание потока под меньший подмассив превышают время выполнения сортировки подмассива. Можно улучшить алгоритм: создавать поток лишь для большего подмассива, а меньший обрабатывать в текущем потоке.
view sourceprint
01.DWORD __stdcall SortMasP (LPVOID p)
02.{
03.lpArrayParam Params = (lpArrayParam)p;
04.if (Params->left>=Params->right) return 0;
05.int left, right, supporting;
06.int temp;
07.int * mas;
08.
09.left=Params->left;
10.right=Params->right;
11.mas = Params->mas;
12.supporting=(((lpArrayParam)p)->left+((lpArrayParam)p)->right)/2;
13.
14.while(Params->left<Params->right)
15.{
16.while ((Params->left<supporting)&&(mas[Params->left]<=mas[supporting]))
17.Params->left++; // Сдвиг левой границы
18.while ((Params->right>supporting)&&(mas[Params->right]>=mas[supporting]))
19.Params->right--; // Сдвиг правой границы
20.// Обмен граничных элементов
21.Swap(&mas[Params->left],&mas[Params->right]);
22.// Обновление индекса опорного элемента
23.if (Params->left == supporting ) supporting = Params->right;
24.else if (Params->right == supporting ) supporting = Params->left;
25.}
26.lpArrayParam Params1 = new ArrayParam;
27.Params1->left=left;
28.Params1->right=supporting-1;
29.Params1->mas = mas;
30.
31.lpArrayParam Params2 = new ArrayParam;
32.Params2->left=supporting+1;
33.Params2->right=right;
34.Params2->mas = mas;
35.
36.if(TCount<pc)
37.{
38.
39.HANDLE thr;
40.InterlockedIncrement(&TCount);
41.
42.if(Params2->right-Params2->left<Params1->right-Params1->left)
43.{
44.thr = CreateThread(0,0,(LPTHREAD_START_ROUTINE)SortMasP, Params1,0,0);
45.SortMasP(Params2);
46.WaitForSingleObject(thr, INFINITE);
47.}
48.else
49.{
50.thr = CreateThread(0,0,(LPTHREAD_START_ROUTINE)SortMasP, Params2,0,0);
51.SortMasP(Params1);
52.WaitForSingleObject(thr, INFINITE);
53.}
54.
55.InterlockedDecrement(&TCount);
56.CloseHandle(thr);
57.
58.}
59.else
60.{
61.SortMasP(Params1);
62.SortMasP(Params2);
63.}
64.
65.delete Params2;
66.delete Params1;
67.return 0;
68.}
Ну, и дополнительные функции/переменные, используемые в методе.
view sourceprint
01.//обмен элементов
02.void Swap(int *a, int *b)
03.{
04.int temp = *a; *a=*b; *b=temp;
05.}
06.
07.DWORD GetProcessorCount()
08.{
09.SYSTEM_INFO si;
10.GetSystemInfo(&si);
11.return si.dwNumberOfProcessors;
12.
13.}
14.
15.DWORD pc=GetProcessorCount(); //число процессоров
16.
17.//структура для передачи параметров
18.typedef struct _ArrayParam
19.{
20.int left;
21.int right;
22.int * mas;
23.
24.} ArrayParam, *lpArrayParam;
25.
26.LONG TCount = 0; //количество созданных потоков
