Пропорційність відрізків хорд і січних кола

Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до кола з даної точки на її зовнішню частину, є число незмінне. Теорема 3. Якщо з точки P до кола проведені дотична, яка проходить через точку дотику A, і січна, яка перетинає коло в точках B і C, то (рисунок 3). Рис. 1 Рис. 2 Рис. 3 Тобто для січної і дотичної, що проведені до кола з однієї точки, квадрат дотичної дорівнює добутку січної на її зовнішню частину. Теорема 4. Хорди, що з’єднують кінці паралельних хорд, рівні.

Вписані й описані чотирикутники

Теорема 1. Нав­коло чотирикутника можна описати коло тоді й тільки тоді, коли сума його протилежних кутів дорівнює . На рисунку . Із цього випливає, що коло можна описати навколо прямокутника (рисунок нижче зліва), зокрема квадрата (рисунок справа), його центром буде точка перетину його діагоналей. Радіус — половина діагоналі. Коло можна описати навколо трапеції тоді й тільки тоді, коли вона є рівнобічною (див. рисунок). Центром кола є точка перетину середніх перпендикулярів до сторін. Навколо паралелограма та трапеції загального виду описати коло не можна. (Зокрема, навколо ромба не можна описати коло.) Теорема 2. Чотирикутник тоді й тільки тоді можна описати навколо кола, якщо суми його протилежних сторін дорівнюють одна ­одній. На рисунку . Отже, коло можна вписати в ромб (зокрема у квадрат), але не можна в прямокутник або паралелограм загального виду. Центр кола, вписаного в ромб, є точкою перетину діагоналей (рисунок нижче зліва). Радіус кола дорівнює половині висоти ромба, а у квадраті — половині сторони (рисунок справа). Зверніть увагу: радіус вписаного в ромб кола (ON) — це висота прямокутного трикутника BOC, яка проведена з вершини прямого кута і має всі властивості висоти прямокутного трикутника, що проведена з вершини прямого кута. Теорема 3. Трапецію тоді й тільки тоді можна описати навколо кола, коли сума її основ дорівнює сумі бічних сторін (рисунок нижче зліва). Центр цього кола — точка перетину бісектрис кутів трапеції. Радіус дорівнює половині висоти трапеції. У випадку рівнобічної трапеції центр вписаного кола лежить на середині висоти трапеції, яка проходить через середини основ (рисунок справа). Бічна сторона трапеції у цьому випадку дорівнює її середній лінії.

Розв’язування трикутників

Теорема косинусів

Теорема (косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін і косинуса кута між ними. У трикутнику, зображеному на рисунку, за теоремою косинусів: . Теорему косинусів зручно застосувати для розв’язування таких задач. 1. Знайти сторону трикутника, якщо відомі дві інші сторони й кут між ними. 2. Знайти косинус кутів трикутника, а отже і самі кути, якщо відомі три сторони трикутника, за формулою . Теорема косинусів дає можливість сформулювати важливі висновки. 1. Відомо, що гострий кут має додатний косинус, а тупий — від’ємний. Отже, квадрат сторони, яка лежить проти тупого кута, більший за суму двох інших сторін, а квадрат сторони, яка лежить проти гострого кута, менший, ніж сума двох інших сторін. 2. Якщо відомі три сторони трикутника, то можна зробити висновок про його вид (гострокутний, тупокутний, прямокутний). Для цього треба порівняти квадрат найбільшої сторони із сумами квадратів двох інших сторін. Якщо квадрат найбільшої сторони трикутника більший, ніж сума квадратів двох інших сторін, трикутник тупокутний, якщо величини рівні — прямокутний, якщо перша величина менша — гострокутний. 3. У випадку, коли трикутник прямокутний, теорема косинусів для сторони, що лежить проти прямого кута, перетворюється на тео­ре­му Піфагора. 4. Із теореми косинусів випливає, що сума квадратів діагоналей паралелограма дорівнює сумі квадратів усіх його сторін. На рисунку . 5. Формула довжини медіани трикутника: у трикутнику, зображеному на рисунку, . 6. Формула довжини бісектриси трикутника: у трикутнику, зображеному на рисунку, . 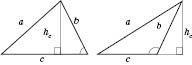7. Формула висоти трикутника: на рисунку нижче зліва зображена висота в гострокутному трикутнику, на рисунку справа — у тупокутному.