12 Структура программы для определения пф механизма чушколомателя

Программа для определения передаточных функций механизма чушколомателя приведена в приложении К.

Отличие этой программы от приведенной в приложении Приложение Д заключается в том, что кроме получения компьютерной модели механизма она позволяет определить ПФ1 и ПФ2 его элементов. В связи с этим линейные и угловые координаты объявлены массивами, так что с помощью функции Graphik могут быть выведены графики ПФ0. Следующий фрагмент программы содержит коэффициенты квадратной матрицы А1[k,r] и элементы вектора В1[k] (формула (Error: Reference source not found)). Процедура Gauss возвращает значения ПФ1 для m положений механизма. Коэффициенты матрицы для определения ПФ2 такие же, как и для определения ПФ1, а элементы вектора В2[k] сформированы на основании формул (11 ОПРЕДЕЛЕНИЕ ПФ1 И ПФ2 ЭЛЕМЕНТОВ МЕХАНИЗМОВ ВЫШЕ ВТОРОГО КЛАССА.6). Значения ПФ2 возвращает функция Gauss. Программа завершается тестированием передаточных функций и выводом графиков ПФ0, ПФ1, ПФ2 элементов механизма.

13 Алгоритмы и программы для определения пф механизмов выше второго класса

Пример 1. Рассмотрим определение передаточных функций элементов механизма, приведенного на рис. 13.1 и содержащего только вращательные КП.

Рисунок.1 – Схема механизма

Этот механизм состоит из начального звена и структурной группы, включающей звенья 2, 3, 4 и 5. Фиктивный механизм с начальным звеном 2 получим, мысленно разрушив звено 4. Тогда, рассматривая начальное звено и структурную группу 1-го вида, включающую звенья 3 и 5, можно определить координаты точек K и F для фиксированного положения точки А кривошипа и различных значений угла j_АВ фиктивного кривошипа 2. Для этого механизма целевая функция имеет вид

. (13.1)

Так как структурная группа рассматриваемого механизма содержит 4 внутренние КП – В, F, C и K, следует записать 8 уравнений связей.

Они имеют вид:

(13.2)

Для определения ПФ1 внутренних КП продифференцируем систему уравнений (13.2) и получим:

(13.3)

При этом было учтено, что 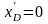и . Для определения коэффициентов матрицы в методе Гаусса в левой части уравнения (13.3) следует записать слагаемые, содержащие неизвестные , , , , , , , , а в правой части – известные слагаемые, содержащие и .

Тогда коэффициенты квадратной матрицы, содержащей восемь строк и восемь столбцов, имеют следующие значения:

A[1,1]=x_B-x_A; A[1,2]=y_B-y_A;

A[2,1]=x_B-x_F; A[2,2]=y_B-y_F; A[2,3]=x_F-x_B; A[2,4]=y_F-y_B;

A[3,3]=x_F-x_A; A[3,4]=y_F-y_A;

A[4,1]=x_B-x_C; A[4,2]=y_B-y_C; A[4,5]=x_C-x_B; A[4,6]=y_C-y_B;

A[5,3]=x_F-x_K; A[5,4]=y_F-y_K; A[5,7]=x_K-x_F; A[5,8]=y_K-y_F;

A[6,5]=x_C-x_D; A[6,6]=y_C-y_D;

A[7,7]=x_K-x_D; A[7,8]=y_K-y_D;

A[8,5]=x_C-x_K; A[8,6]=y_C-y_K; A[8,7]=x_K-x_C; A[8,8]=y_K-y_C.

Остальные коэффициенты матрицы равны нулю.

Свободные члены матрицы В1 системы уравнений имеют вид:

B1[1]=(x_B-x_A) + (y_B-y_A) ;

B1[2]=0;

B1[3]= (x_F-x_A) + (y_F-y_A) ;

B1[4]=0;

B1[5]=0;

B1[6]=0;

B1[7]=0;

B1[8]=0.

Для определения ПФ2 внутренних КП продифференцируем систему уравнений (13.3) и получим:

(13.4)

Далее систему (13.4) следует записать так, чтобы в левой части каждого уравнения оказались слагаемые, содержащие неизвестные , , , , , , , , а в правой части – слагаемые, содержащие известные , .

Нетрудно заметить, что коэффициенты квадратной матрицы для определения ПФ2 такие же, как и для определения ПФ1, а свободные члены В2 системы уравнений имеют вид:

В2[1]= ;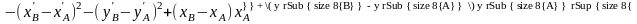

B2[2]= ;

B2[3]=

B2[4]=

B2[5]=

B2[6]=

B2[7]=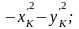

B2[8]=

Листинг программы для определения ПФ рассматриваемого механизма приведен в приложении Л.

Пример 2. Определим передаточные функции механизма, содержащего кинематическую пару «кулиса-камень» и представленного на рис. 13.2.

Рисунок 13.2 – Схема механизма с кулисной парой

Этот механизм по классификации Ассура-Артоболевского является механизмом 3-го класса, так как содержит четырехзвенную структурную группу, включающую базовое звено 3 и звенья 2, 4 и 5. Листинг программы для определения ПФ элементов этого механизма приведен в приложении М.

Для определения ПФ0 элементов этого механизма, а именно х_В, y_B и х_С , в результате мысленного разрушения звена 4 получим фиктивный механизм с кривошипом 2 и группой Ассура второго вида, содержащей звенья 3 и 5.

Тогда целевая функция имеет вид

CF=Y_B-Y_D-(X_B-X_D)tgj_BD.

Для определения ПФ1 , и следует записать три уравнения связей. Два из них имеют следующий вид:

; (13.5)

. (13.6)

Третье уравнение может быть записано следующим образом:

j_BD=j_BC-a_B,

с учетом того, что для рассматриваемой схемы j_BD<0, j_BC<0 и a_B>0.

Тогда , или .

Учитывая, что 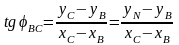, и обозначив tga_B=k, окончательно получим

(y_D - y_B)[(x_C - x_B) + k(y_N -y_B)]=(x_D - x_B)[(y_N - y_B) - k(x_C - x_B)]. (13.7)

Для определения неизвестных ПФ1 продифференцируем уравнения (13.5)…(13.7).

С учетом того, что , и , получим:

(13.8)

Систему уравнений записываем в форме, удобной для определения элементов квадратной матрицы:

(13.9)

Тогда элементы квадратной матрицы для определения ПФ1 элементов структурной группы:

A[1,1]=x_B-x_A; A[1,2]=y_B-y_A; A[1,3]=0;

A[2,1]=x_B-x_С; A[2,2]=y_B-y_N; A[2,3]=x_C-x_B;

A[3,1]=y_N-y_D+k(2x_B-x_C-x_D);

A[3,2]=x_D-x_C+k(2y_B-y_N-y_D);

A[3,3]=y_D-y_B+k(x_D-x_B).

Правые части системы уравнений имеют вид:

B1[1]= ;

B1[2]=0;

B1[3]=0.

Продифференцировав уравнения (13.9) ещё раз, получим систему линейных уравнений для определения ПФ2 элементов структурной группы, которая в результате преобразований принимает следующий вид:

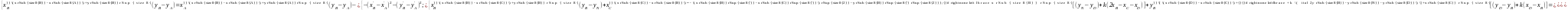(13.10)

Замечаем, что элементы квадратной матрицы для определения ПФ2 элементов структурной группы такие же, как и для определения ПФ1.

Правые части системы уравнений имеют вид:

В2[1]=

B2[2]=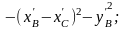

B2[3]= .

Пример 3. Рассмотрим определение ПФ механизма, представленного на рис. 13.3.

Рисунок 13.3 – Схема механизма

Листинг программы для расчета этого механизма приведен в приложении Н.

Рассматриваемый механизм содержит шестизвенную структурную группу, содержащую два базовых звена 3 и 5 и четыре поводка 2, 4, 6 и 7. Для построения компьютерной модели механизма мысленно разрушим звено 7 и рассмотрим фиктивный механизм с формулой строения

(0-2)®(3-4)_1®(5-6)₁ .

Используя стандартные процедуры As1 и Poi, определяем координаты точки F. Целевая функция имеет вид

.

Так как рассматриваемая структурная группа имеет пять внутренних КП, можно записать десять уравнений связей вида

и т.д.

Для определения линейных ПФ1 осей вращательных КП следует продифференцировать эти уравнения и получить десять уравнений вида

и т.д.

При этом известными величинами являются , , а также , , , , , 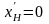. После переноса известных величин в правые части системы десяти уравнений получим коэффициенты квадратной матрицы:

A[1,1]=x_A-x_B; A[1,2]=y_A-y_B;

A[2,1]=x_B-x_C; A[2,2]=y_A-y_B; A[2,3]=x_C-x_B; A[2,4]=y_C-y_B;

A[3,1]=x_B-x_D; A[3,2]=y_B-y_D; A[3,5]=x_D-x_B; A[3,6]=y_D-y_B;

A[4,3]=x_D-x_C; A[4,4]=y_D-y_C; A[4,5]=x_C-x_D; A[4,6]=y_C-y_D;

A[5,5]=x_D-x_E; A[5,6]=y_D-y_E;

A[6,3]=x_C-x_F; A[6,4]=y_C-y_F; A[6,9]=x_F-x_C; A[6,10]=y_F-y_C;

A[7,3]=x_C-x_K; A[7,4]=y_C-y_K; A[7,7]=x_K-x_C; A[7,8]=y_K-y_C;

A[8,7]=x_K-x_F; A[8,8]=y_K-y_F; A[8,9]=x_F-x_K; A[8,10]=y_F-y_K;

A[9,7]=x_K-x_G; A[9,8]=y_K-y_G;

A[10,9]=x_F-x_H; A[10,10]=y_F-y_H.

Остальные коэффициенты равны нулю. Правая часть первого уравнения системы B1[1]= . Остальные B1 равны нулю. С помощью процедуры Gauss определяем , , , , , , , , ,  .

В результате повторного дифференцирования получим систему десяти уравнений для определения ПФ2 в форме:

;

.

При этом известными являются все ПФ1, а также и , кроме того, , , , , , .

Тогда коэффициенты квадратной матрицы для определения ПФ2 такие же, как и для определения ПФ1.

Правые части уравнений имеют вид:

;

;

;

;

;

;

;

;

;

.

С помощью процедуры Gauss определяем , , , , , , , , , .

После этого в программе выполняется тестирование всех ПФ.

Пример 4. Рассмотрим методику определения передаточных функций кулисно-рычажного гиперболографа Вяткина, представленного на рис. .8. В соответствии с формулой строения этого механизма к начальному звену 1 параллельно присоединены две двухзвенные группы четвертого вида, а затем двухзвенная группа первого вида. Присоединенная затем четырехзвенная структурная группа показана на рис. .9. Листинг программы для расчета этого механизма приведен в приложении П.

Как видно из программы, расчет кривошипа, двух структурных групп четвертого вида и группы первого вида выполнен с помощью стандартных процедур, используемых для расчета механизмов второго класса. В результате определяем передаточные функции внешних КП: линейные ПФ точки В и угловые ПФ звена 7. После этого могут быть определены ПФ0 элементов четырехзвенной структурной группы.

В качестве кривошипа фиктивного механизма принимаем звено 11. Тогда присоединенной структурной группой является двухзвенная группа второго вида, включающая звенья 8 и 10.

Поскольку Ð DEK=90°, то целевая функция имеет вид CF=sin(j_OC-j_DE). Так как задача по определению ПФ1 или ПФ2 элементов группы содержит по шесть неизвестных (по две линейные ПФ точек D, E и K), следует записать шесть уравнений связей

(13.11)

Для определения ПФ1 продифференцируем эти уравнения:

(13.12)

После преобразования этих уравнений получим коэффициенты матрицы для реализации методом Гаусса:

A [1,1]=x_D-x_B; A[1,2]=y_D-y_B;

A[2,1]=x_D-x_E; A[2,2]=y_D-y_E; A[2,3]=x_E-x_D; A[2,4]=y_E-y_D;

A[3,1]=tgj₇; A[3,2]=-1; A[3,3]=-tgj₇; A[3,4]=1;

A[4,3]=1; A[4,4]=-ctgj₁; (13.13)

A[5,3]=1; A[5,4]=tgj₇; A[5,5]=-1; A[5,6]=-tgj₇

A[6,5]=tgj₇; A[6,6]=-1.

Остальные коэффициенты равны нулю.

Правые части уравнений:

;

;

;

;

.

Для определения ПФ2 продифференцируем уравнения (13.12) и получим

(13.14)

После преобразования этих уравнений получим коэффициенты матрицы для определения ПФ2 элементов группы, аналогичные коэффициентам (13.13). При этом правые части уравнений имеют вид:

;

;

;

;

;

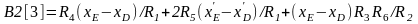где ; ; ;

; ; ;

; ; ;

.
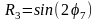