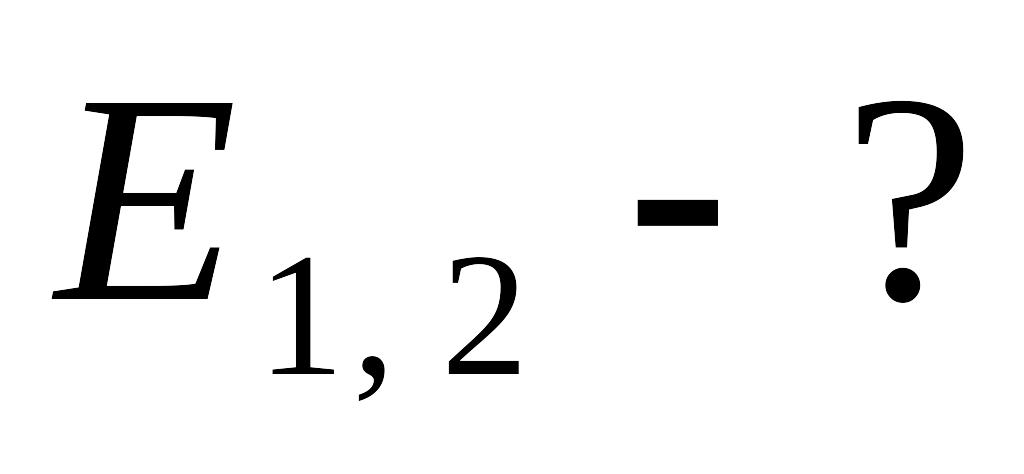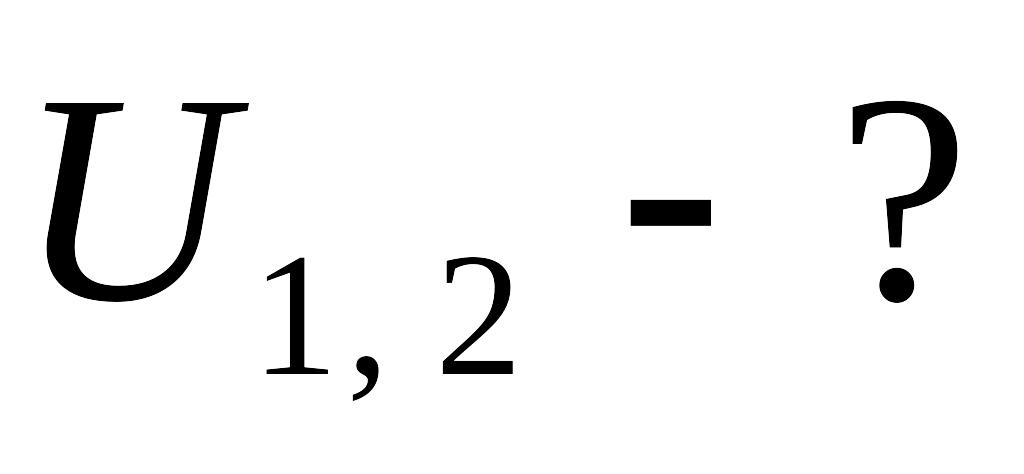- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •405. По проводнику, согнутому в виде прямоугольника со сторонами 6 и 10 см, течёт ток силой 20 а. Определить напряжённость и индукцию магнитного поля в точке пересечения диагоналей прямоугольника.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •610. Красная граница фотоэффекта для цезия равна 620 нм. Определить кинетическую энергию и скорость фотоэлектронов при освещении цезия монохроматическим светом с длиной волны 0,505 мкм.
- •Решение.
- •Решение.
306. Тонкое
кольцо радиуса
![]() см несёт равномерно распределённый
заряд
см несёт равномерно распределённый
заряд
![]() мкКл. На перпендикуляре к плоскости
кольца, восстановленном из его середины,
находится точечный заряд
мкКл. На перпендикуляре к плоскости
кольца, восстановленном из его середины,
находится точечный заряд
![]() мкКл. Определить силу, действующую на
точечный заряд со стороны заряженного
кольца, если он удален от центра кольца:
мкКл. Определить силу, действующую на
точечный заряд со стороны заряженного
кольца, если он удален от центра кольца:
1) на
![]() см;
см;
2) на
![]() м.
м.
-
Дано:
см
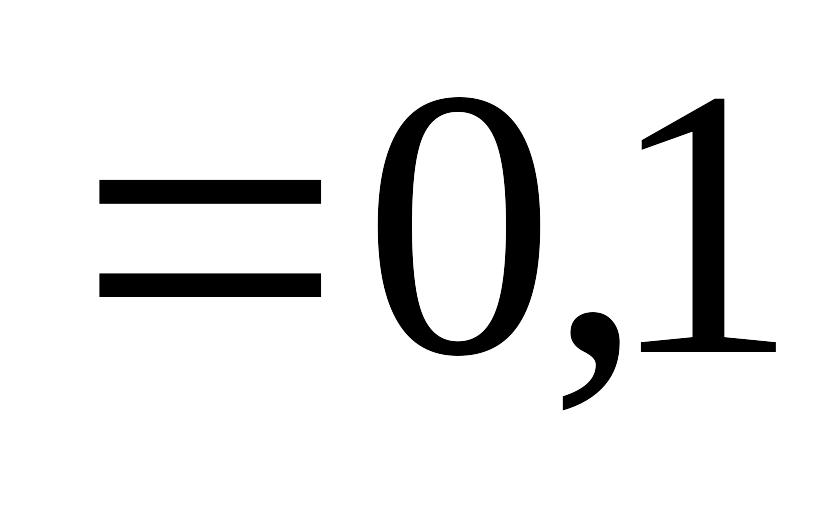 м
ммкКл
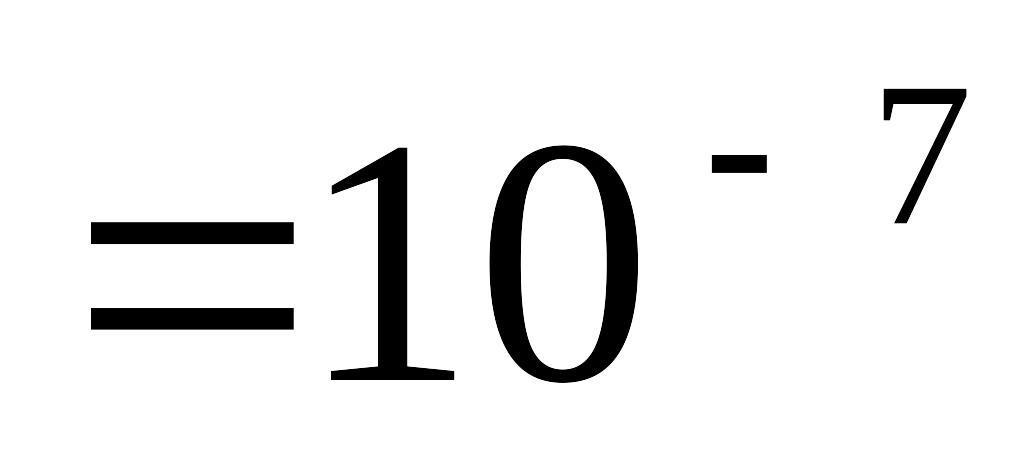 Кл
КлмкКл
 Кл
Клсм
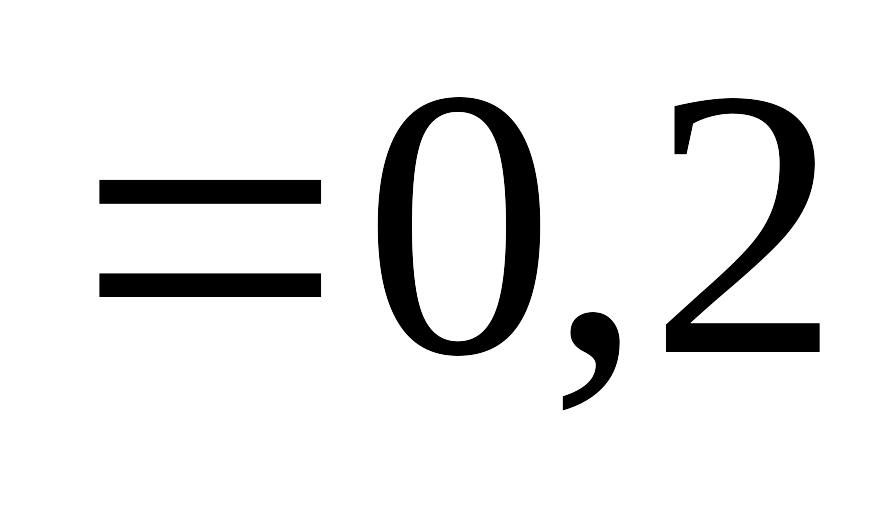 м
мм
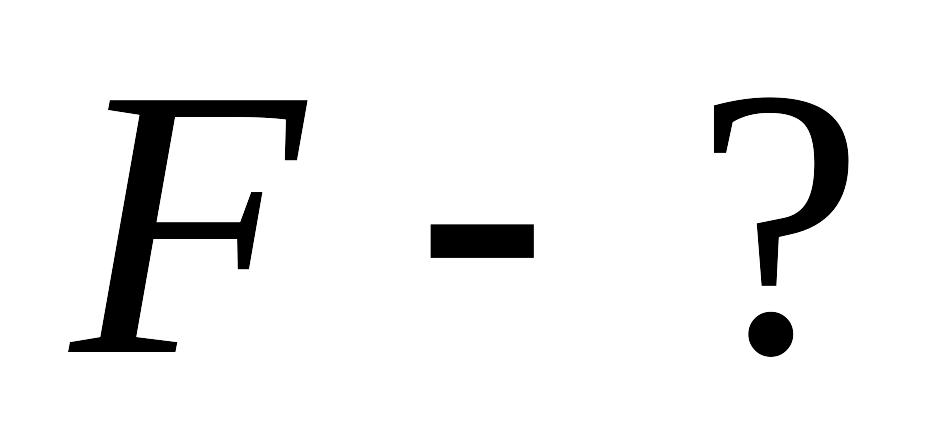
Решение.
Определим напряжённость поля в точке
![]() ,
расположенной на оси кольца на расстоянии
,
расположенной на оси кольца на расстоянии
![]() от его центра.
от его центра.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Линейная плотность заряда на кольце:
![]() ,
,
где
![]() – заряд кольца;
– заряд кольца;
![]() – длина кольца.
– длина кольца.
Рассмотрим малый участок кольца
![]() .
.
Его заряд:
![]() .
.
Расстояние от любого участка кольца до точки :
![]() ,
,
где – радиус кольца.
Участок создаёт в точке напряжённость:
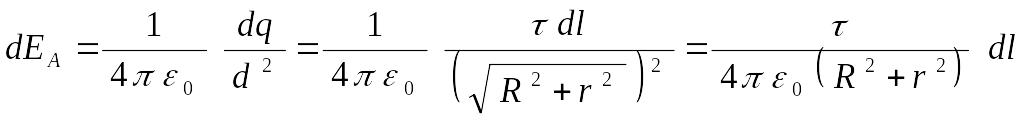 ,
,
где
![]() Ф/м – электрическая постоянная.
Ф/м – электрическая постоянная.
Вектор напряжённости
разложим на две составляющие –
перпендикулярную плоскости кольца
![]() и параллельную плоскости кольца
и параллельную плоскости кольца
![]() :
:
![]() ,
,
![]() ,
,
где
![]() .
.
Любые два противоположных участка будут
создавать в точке
напряжённости
,
составляющие которых
и
![]() будут равны по величине и противоположны
по направлению, и которые попарно
компенсируются. Составляющая
будут равны по величине и противоположны
по направлению, и которые попарно
компенсируются. Составляющая
![]() результирующей напряжённости
результирующей напряжённости
![]() ,
создаваемой в точке
всем кольцом, будет равна 0, поэтому:
,
создаваемой в точке
всем кольцом, будет равна 0, поэтому:
![]() .
.
По принципу суперпозиции имеем:
![]() .
.
Поскольку все векторы
![]() направлены вдоль одной прямой
,
то векторную сумму можно заменить
алгебраической:
направлены вдоль одной прямой
,
то векторную сумму можно заменить
алгебраической:
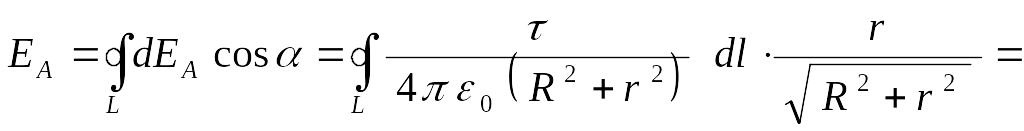
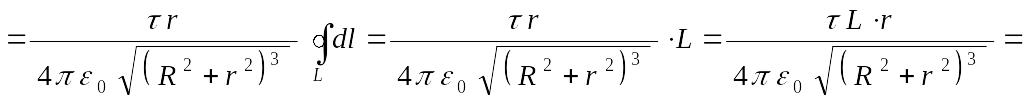
 .
.
Тогда сила, с которой действует кольцо
на точечный заряд
![]() ,
находящийся в точке
(поскольку заряды
и
одного знака, то это сила отталкивания):
,
находящийся в точке
(поскольку заряды
и
одного знака, то это сила отталкивания):
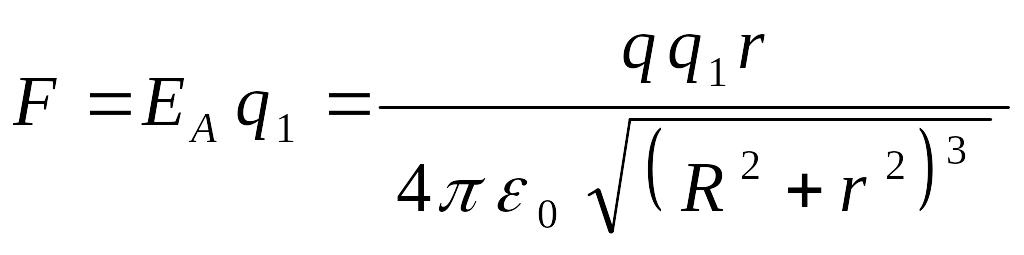 .
.
1) см.
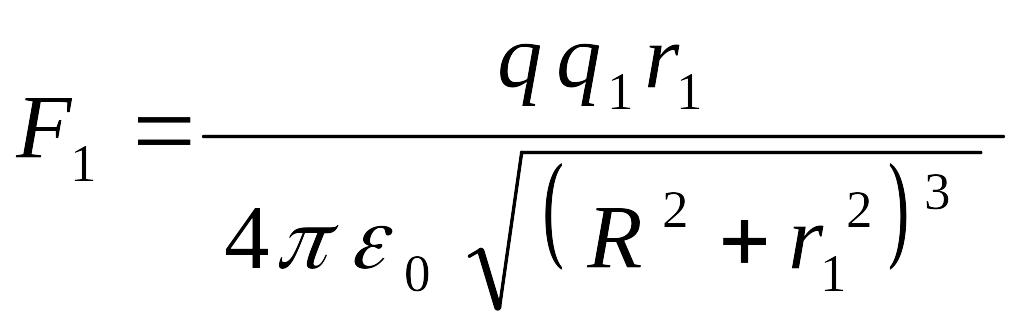 ;
;
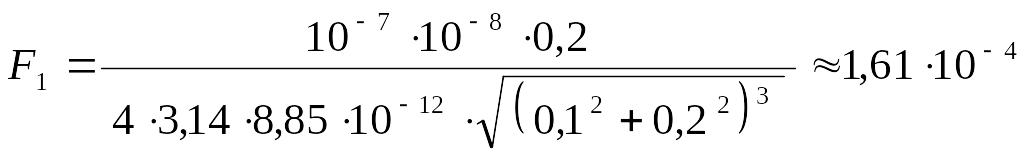 Н
Н
![]() мкН.
мкН.
2) см.
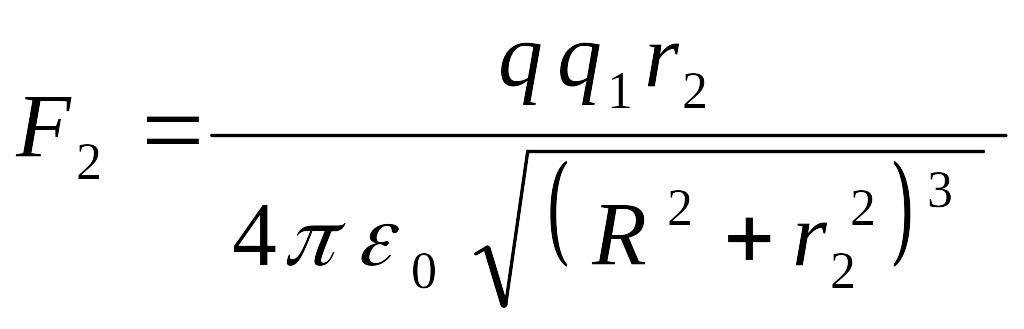 ;
;
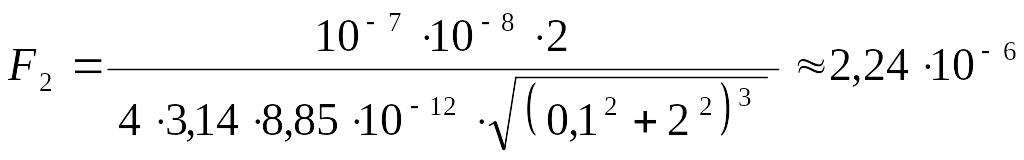 Н
Н
![]() мкН.
мкН.
Заметим, что поскольку
![]() ,
то кольцо в этом случае можно считать
точечным зарядом и силу взаимодействия
найти по закону Кулона:
,
то кольцо в этом случае можно считать
точечным зарядом и силу взаимодействия
найти по закону Кулона:
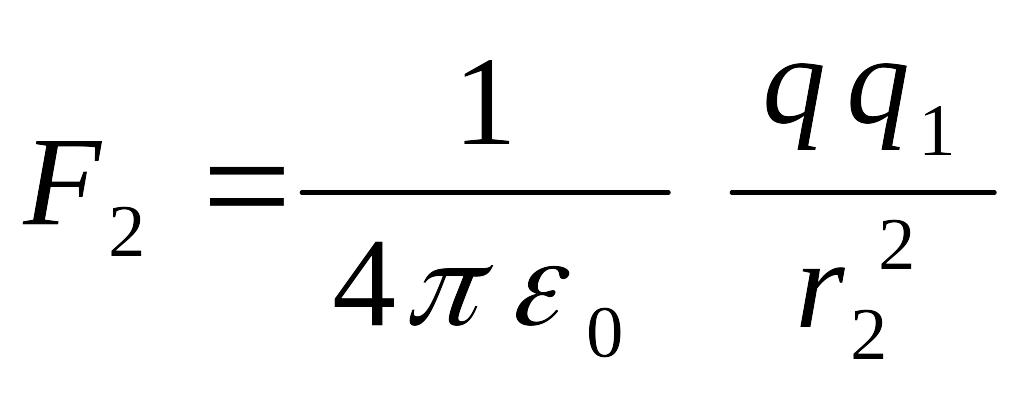 ;
;
![]() Н
Н
![]() мкН.
мкН.
Ответ: 1)
![]() мкН; 2)
мкН; 2)
![]() мкН.
мкН.
308. С какой силой (на единицу длины)
взаимодействуют две заряженные бесконечно
длинные параллельные нити с одинаковой
линейной плотностью заряда, равной
![]() Кл/м, находящиеся на расстоянии 4 см друг
от друга?
Кл/м, находящиеся на расстоянии 4 см друг
от друга?
-
Дано:
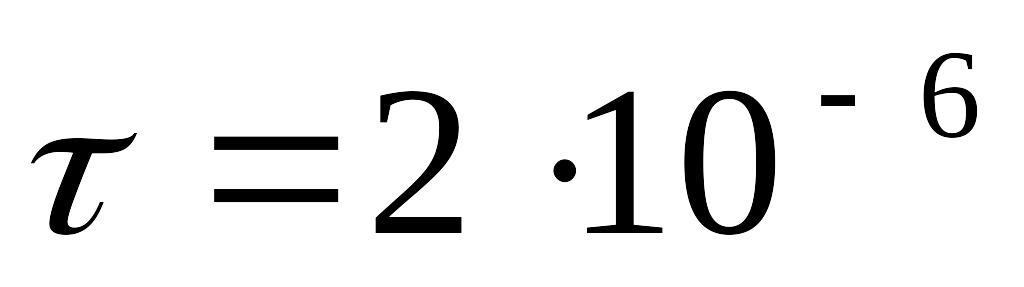 Кл/м
Кл/м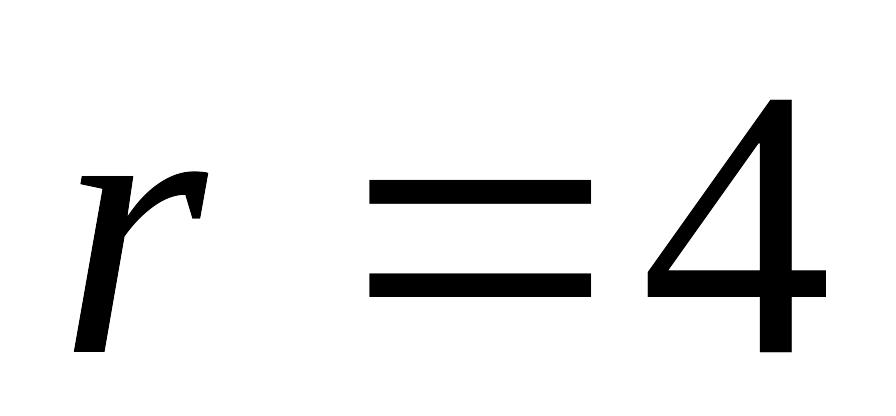 см
см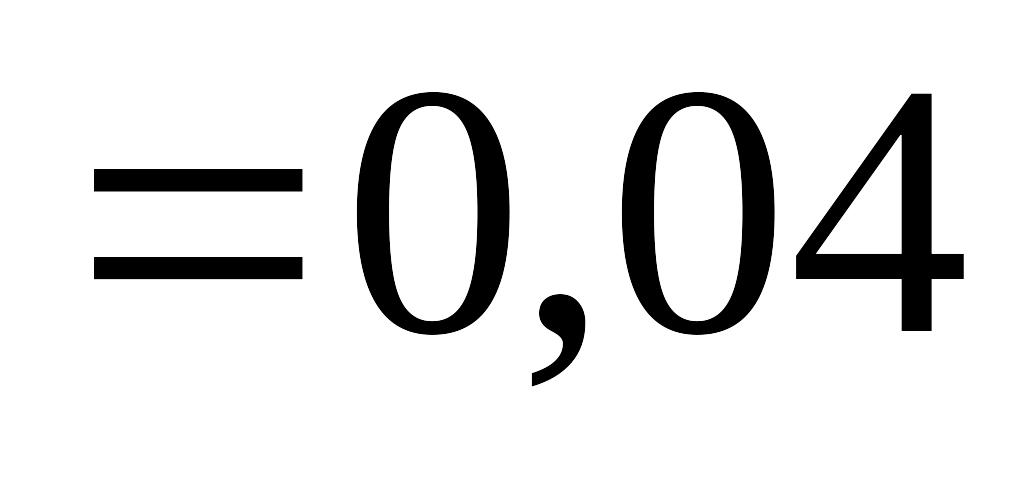 м
м
Решение.
Будем считать, что нить 1 находится в поле, созданном нитью 2.
Нить 1 Нить 2

![]()
Напряжённость поля нити 2 можно найти по формуле для бесконечного равномерно заряженного цилиндра с бесконечно малым радиусом:
![]() ,
,
где
![]() – электрическая постоянная;
– электрическая постоянная;
![]() – линейная плотность заряда
нити;
– линейная плотность заряда
нити;
– расстояние от точки до нити.
Заряд малого элемента нити 1:
![]() .
.
На малый элемент нити 1 действует сила:
![]() .
.
Тогда сила, действующая на единицу длины нити:
![]() ;
;
![]() Н/м.
Н/м.
Ответ:
![]() Н/м.
Н/м.
315. Поле образовано бесконечной
равномерно заряженной плоскостью с
поверхностной плотностью заряда
![]() Кл/м
Кл/м![]() .
Определить разность потенциалов двух
точек поля, отстоящих от плоскости на
5 и на 10 см.
.
Определить разность потенциалов двух
точек поля, отстоящих от плоскости на
5 и на 10 см.
-
Дано:
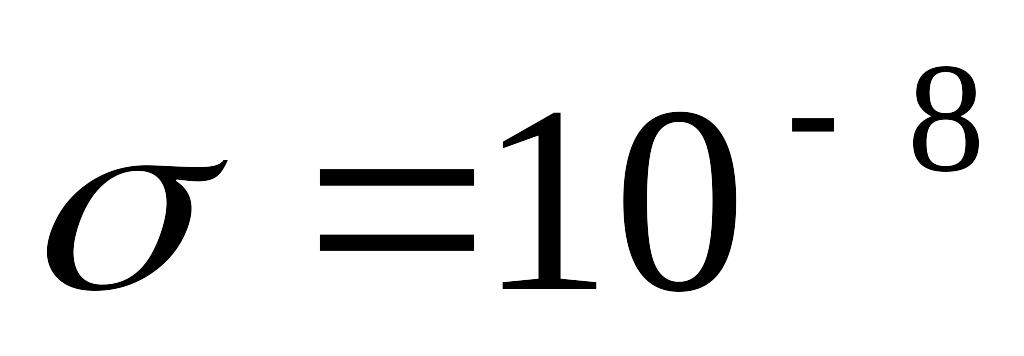 Кл/м
Кл/м
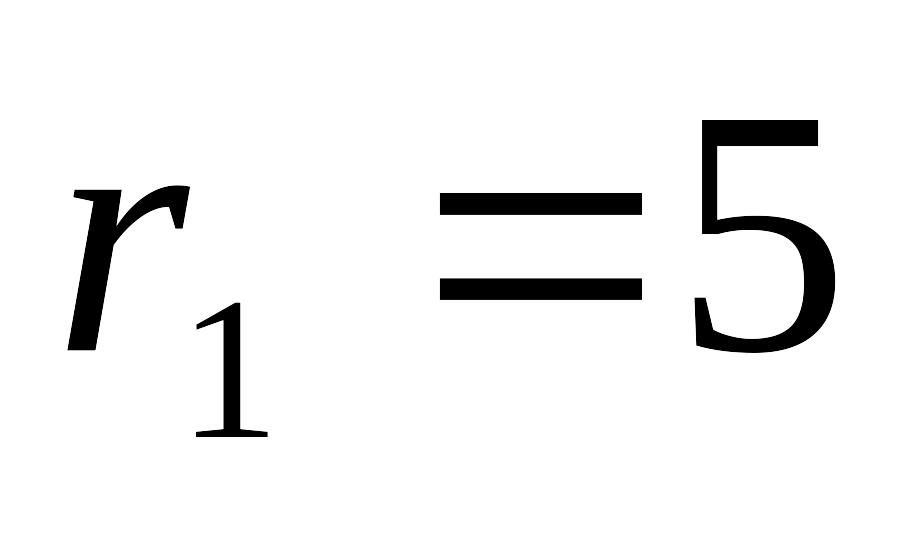 см
см м
м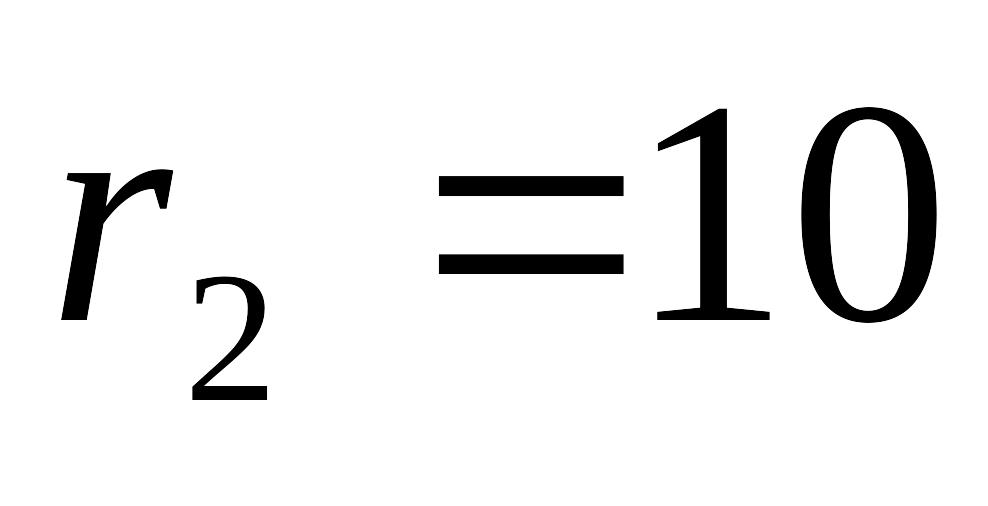 мм
мм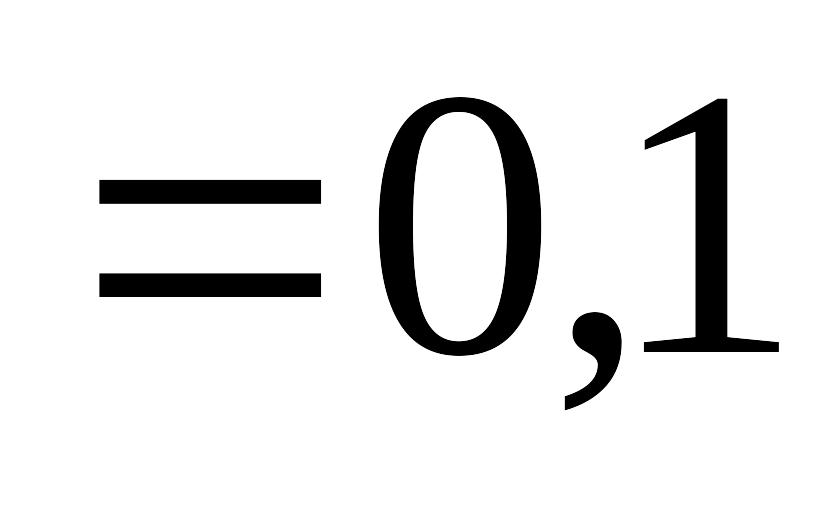 м
м
Решение.
Напряжённость поля бесконечной равномерно заряженной плоскости:
![]() ,
,
где
![]() – поверхностная плотность заряда
плоскости;
– поверхностная плотность заряда
плоскости;
![]() – электрическая постоянная.
– электрическая постоянная.
Разность потенциалов между точками,
отстоящими от плоскости на
![]() и
и
![]() :
:
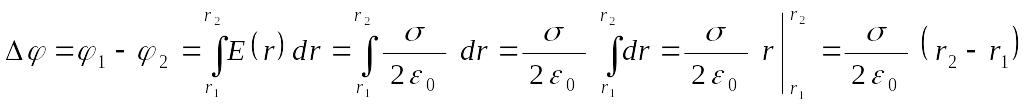 ;
;
![]() В.
В.
Ответ:
![]() В.
В.
320. Электрон, обладающий кинетической энергией 5 эВ, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов 2 В?
-
Дано:
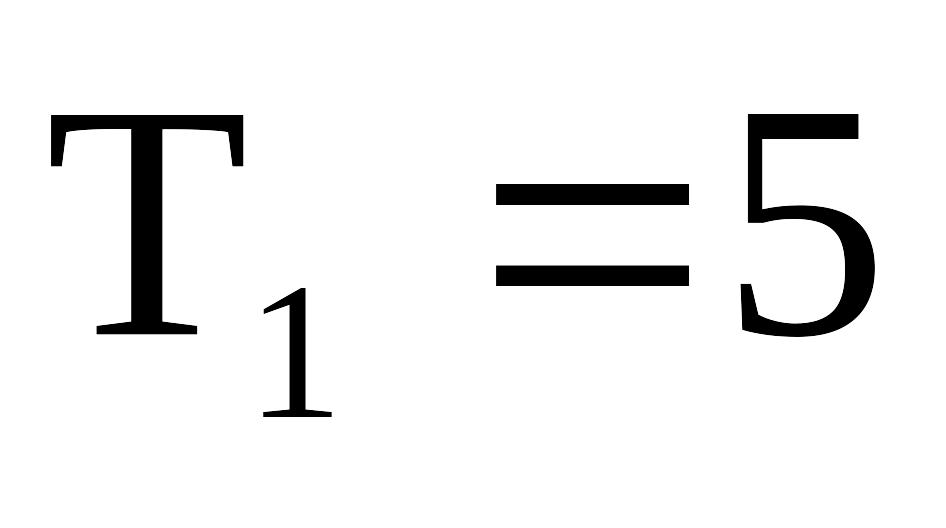 эВ
эВ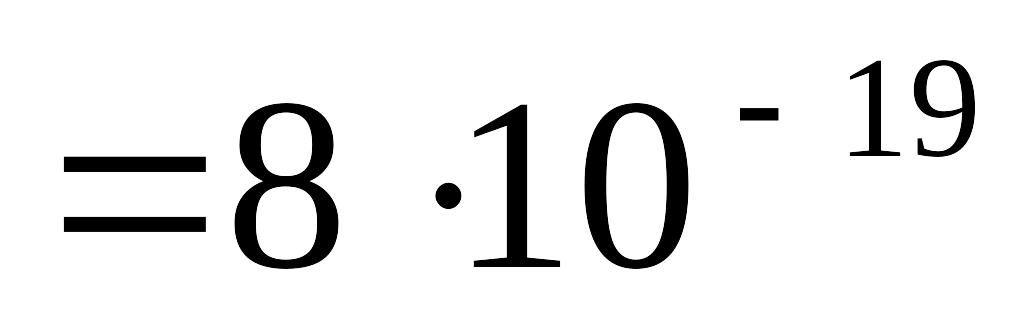 эВ
эВ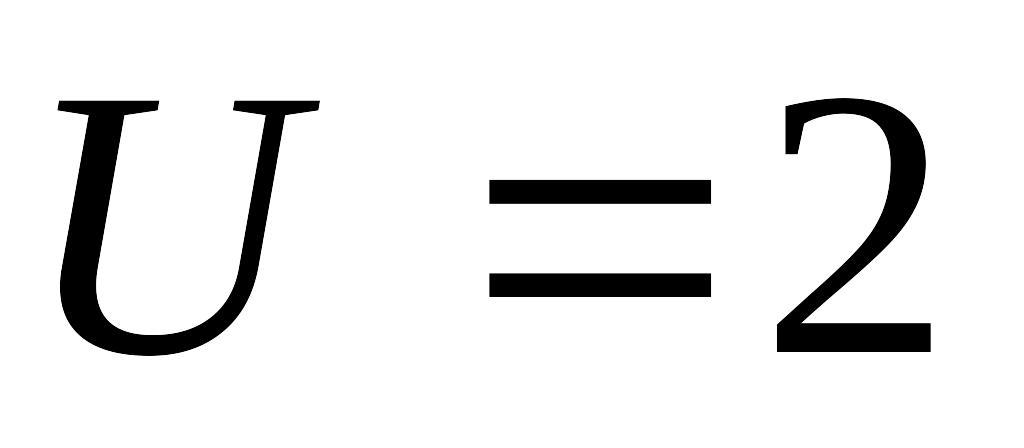 В
В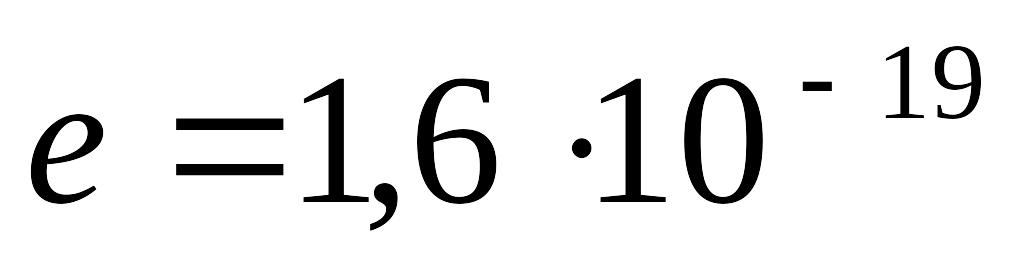 Кл
Кл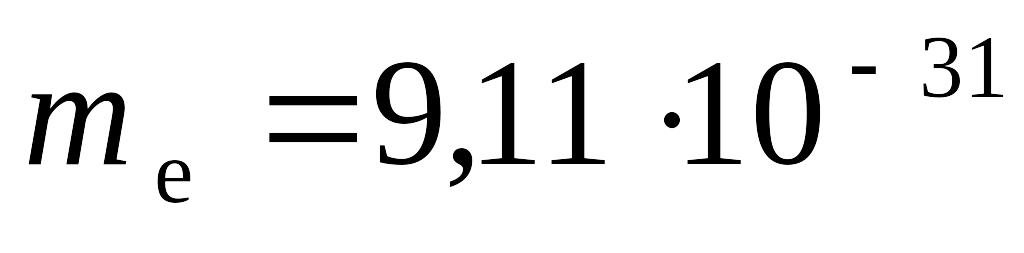 кг
кг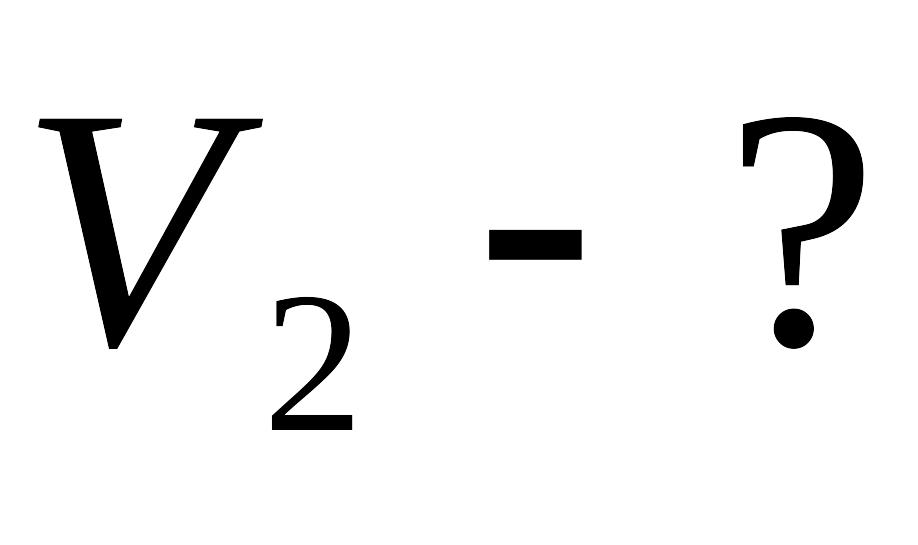
Решение.
Работа, которую силы поля совершают над электроном:
![]() ,
,
где
![]() – заряд электрона;
– заряд электрона;
![]() – разность потенциалов, пройденная
электроном.
– разность потенциалов, пройденная
электроном.

![]()
![]()
![]()
Начальная кинетическая энергия электрона
![]() ,
конечная –
,
конечная –
![]() .
На электрон действует тормозящая сила
Кулона
.
Следовательно, по закону сохранения
энергии:
.
На электрон действует тормозящая сила
Кулона
.
Следовательно, по закону сохранения
энергии:
![]() .
.
С другой стороны, кинетическая энергия электрона:
![]() ,
,
где
![]() – масса электрона;
– масса электрона;
![]() – конечная скорость электрона.
– конечная скорость электрона.
Найдём конечную скорость электрона:
![]() ;
;
![]() ;
;
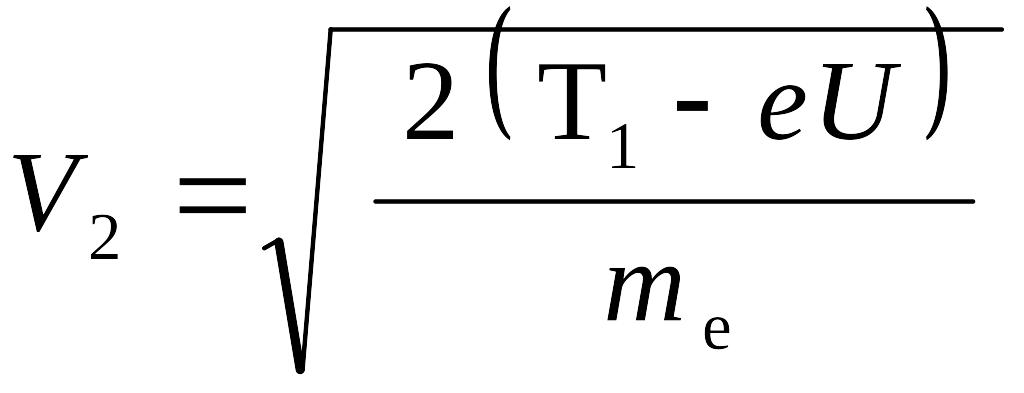 ;
;
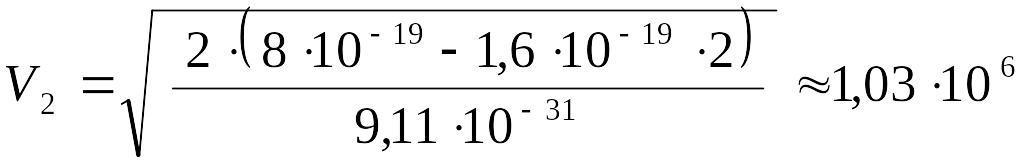 м/с.
м/с.
Ответ:
![]() м/с.
м/с.
326. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектриков – слоем стекла толщиной 1 см и слоем парафина толщиной 2 см. Разность потенциалов между обкладками равна 3000 В. Определить напряжённость поля и падение потенциала в каждом из слоёв.
-
Дано:
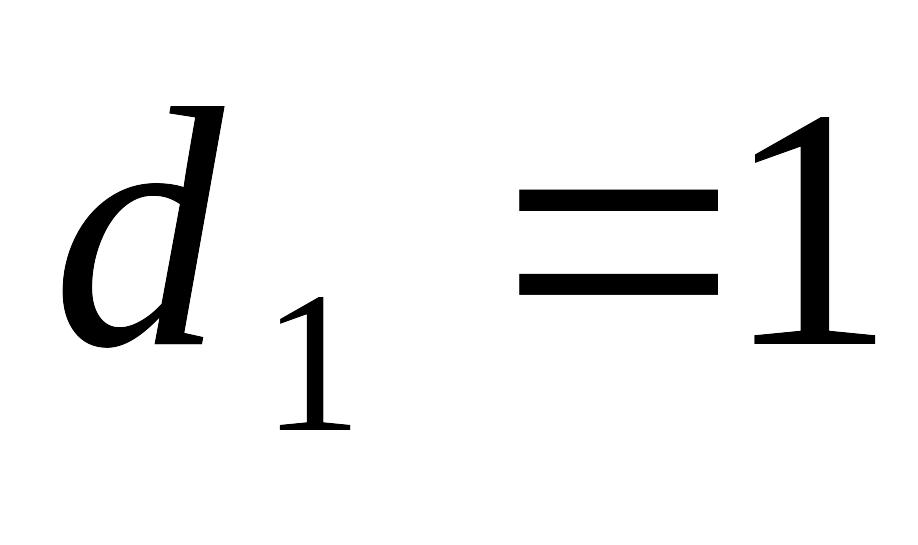 см
см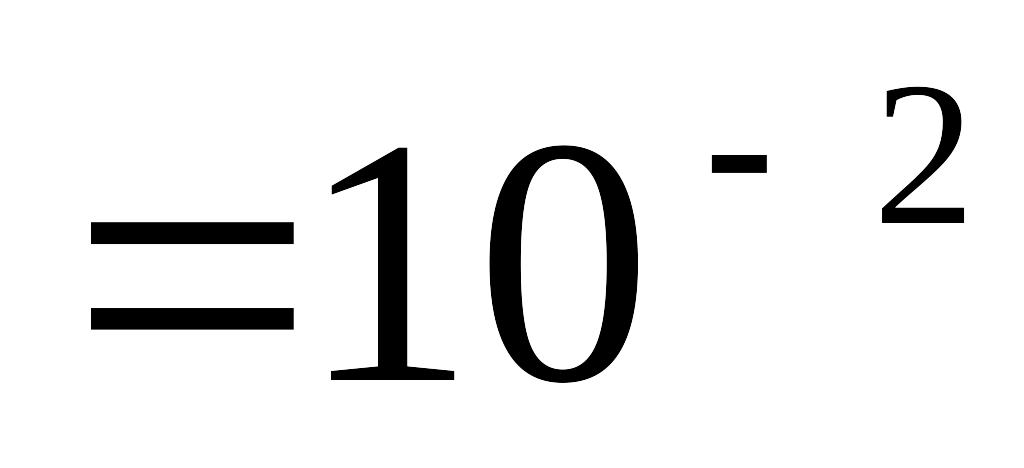 м
м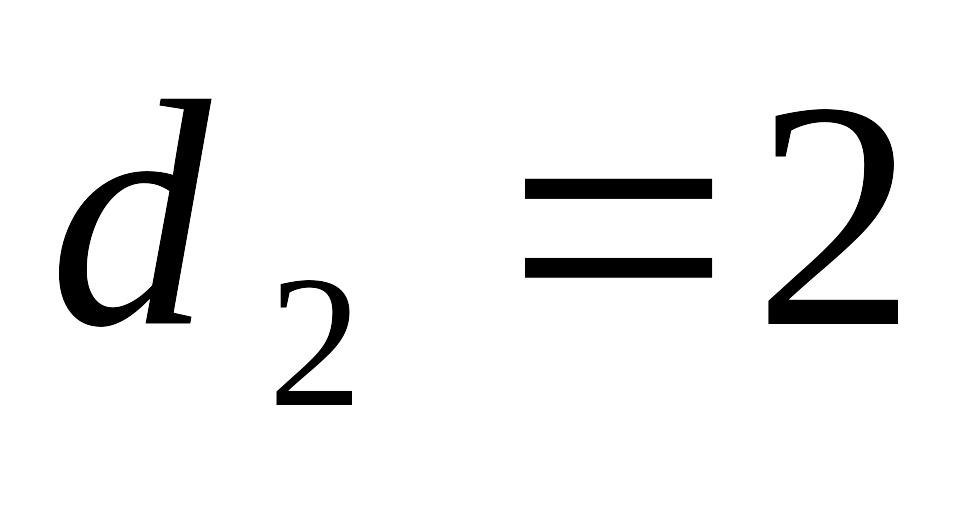 см
см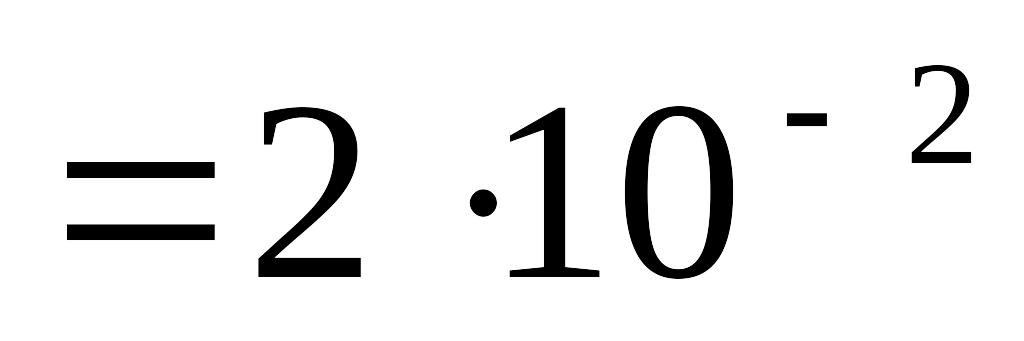 м
м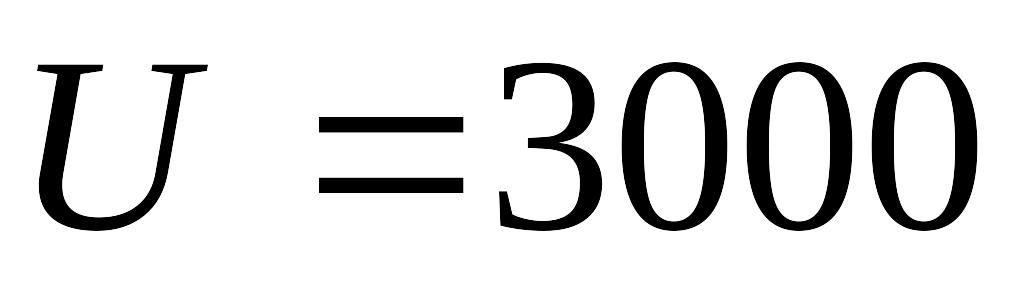 В
В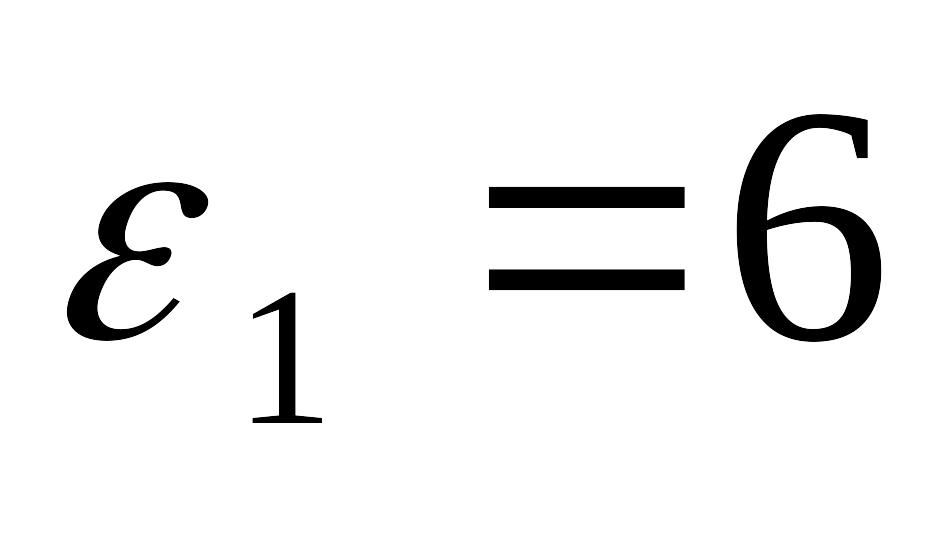
Это справочные величины, но их значения могут
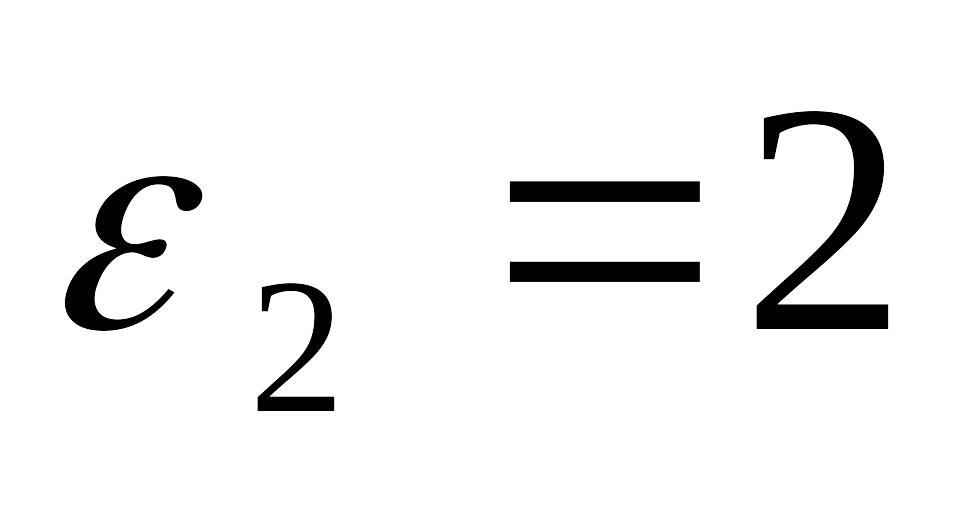
отличаться (сравнить с методичкой – вдруг есть)