Методом элементарных преобразований.

• Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу , ;

• прибавление к любой строке матрицы другой строки, умноженной на константу , .

9. Нахождение обратной матрицы при помощи элементарных преобразований.

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1.

10. Системы линейных уравнений. Формулы Крамера.

• Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[1].

• Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.

• Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

• Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.

• Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

11. Теорема Кронекера-Капелли.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

12. Решение произвольных систем. Метод Жордана-Гаусса.

13. Однородные системы линейных уравнений. Фундаментальная система решений.

14. Векторы в пространстве и на плоскости. Линейные операции над векторами.

• Вектор – отрезок, имеющий направление.

• Умножение на скаляр (направление совпадает, модель умножается), дистрибутивность канает.

• Умножение на 0-ой вектор.

• На -1. Получится противоположно направленный.

• a=kb (a||b)

• Сложение по правилу треугольника и параллелаграмма.

15. Скалярное, векторное и смешанное произведения векторов и их свойства.

Все определения делал Джигурда!!! Читаем формулу, получаем определение 0_о.

Вектороное – вектор перпендикулярен плоскости и тройка правая.

Все есть в теор. вопросах.

16. Линейное пространство. Определение, 8 аксиом.

Линейное пространство, он же векторное.

Множество L называется линейным пространством, если:

1. Определена операция сложения. x,y из L. x+y;

2. Определена операция умножения на число.a*x, где a любое вещественное или комплексное число.

Аксиомы в числе 8 штук:

1. x+y=y+x; коммутативность

2. (x+y)+z=x+(y+z); ассоциативность сложения

3. a(bx)=(ab)x ассоциативность умножения на число

4. a(x+y)=ax+by; a-число; дистрибутивность по отношению сложения элементов L

5. (a+b)x=ax+bx; a,b-числа; дистрибутивность к сложению чисел

6. Существуют элементы нулевой элемент: x+0=x;

7. x*1=x; для любого х;

8. Существует противопожное число: x+(-x)=0;

17. Линейно зависимые и линейно независимые системы векторов.

Есть в другом файле.

18. Базис и размерность линейного пространства. Координаты вектора.

• Число элементов (мощность) максимального линейно независимого подмножества пространства не зависит от выбора этого подмножества и называется рангом, или размерностью, пространства, а само это подмножество — базисом (базисом Га́меля или линейным базисом). Элементы базиса также называют базисными векторами. Свойства базиса:

• Базис пространства образует система л. независимых векторов в числе размерности пространства.

• Базис R³ (i,j,k) ортогональный, определяющий правую тройку векторов.

• Любой вектор можно единственным образом представить в виде линейной комбинации базиса(разложения по базису)

• Для i,j,k – a=xi+yj+zk; x,y,z-координаты вектора. Если базис ортогонален, то координаты совпадают с проекциями на рси.

19. Основные уравнения плоскости. Уравнение плоскости, проходящей через три точки.

• Общее- через нормальный вектор и точку. A(x-x0)+B(y-y0)+C(z-z0)=0;

• Через 3 точки: Запилить 3 вектора через 3 этих точки и висячую точку и запилить смешанное произведение, т.к. они комплонарны и будет все за..сь.

• В отрезках: Поделить общее на –D и тоже все будет ок.

• Нормальное- поделить все на длину вектора нормали.

20. Уравнения прямой в пространстве. Уравнение прямой, проходящей через две точки. Угол между плоскостями, прямыми, прямой и плоскостью. Условия параллельности и перпендикулярности.

• Уравнения прямой в пространстве, проходящей через две заданные точки 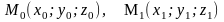, имеют вид

.

• Угол между плоскостями как угол между векторами нормали.

• Угол между прямой 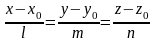и плоскостью 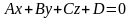определяется по формуле (угол между направляющим и нормальным векторами.

;

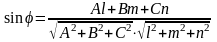условие параллельности прямой и плоскости: скалярное произведение

;

условие перпендикулярности прямой и плоскости: условие колллинеарности 2-х векторов.

.

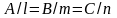21. Основные уравнения прямой на плоскости.

• Через пересечение 2-х плоскостей. Система из 2-х уравнений.

• Каноническо- через направ вектор и точку.

• Параметрическое.

• Через 2 точки.

22. Канонические уравнения кривых второго порядка.

• Эллипсом называется множество всех точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (ее обозначают через 2а), причем эта постоянная больше расстояния между фокусами.

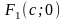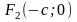Если оси координат расположены по отношению к эллипсу так, как на рисунке 11, а фокусы эллипса находятся на оси Ох на равных расстояниях от начала координат в точках и , то получится простейшее (каноническое) уравнение эллипса:

.

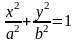• Гиперболой называется множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (ее обозначают через 2а), причем эта постоянная меньше расстояния между фокусами.

Если поместить фокусы гиперболы в точках и , то получим каноническое уравнение гиперболы

,

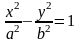• Параболой называется множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Если директрисой параболы является прямая 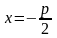, а фокусом – точка , то уравнение параболы имеет вид

.

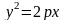М атан