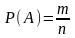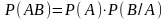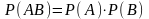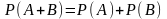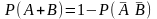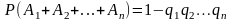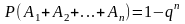Лекция 1. Основные понятия теории вероятностей
Испытание и событие − это основные понятия теории вероятностей.
Испытание − опыт, наблюдение, эксперимент, реализация определенного комплекса условий.
Событие − результат, исход испытания.
События |
Достоверное (U) − обязательно произойдет.
Невозможное (V) − заведомо не произойдет.
Случайное (A,B,C…) − может либо произойти, либо не произойти.
Примеры случайных событий.
Испытание |
Случайное событие |
1. Бросание монеты. 2. Бросание игральной кости.
3. Стрельба по мишени.
4. Извлечение шара из урны.
5. Проверка качества изделий.
6. Рождение ребенка. |
Появление герба или цифры. Выпадение какого-либо числа очков. Попадание, промах, выбивание определенного числа очков. Появление шара определенного цвета или номера. Изделие бракованное или стандартное. Пол ребенка. |
 Виды случайных
событий.
Виды случайных
событий.
Определение 1. Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании. В противном случае события называются несовместными.
Примеры.__________________________________________________________
1) Испытание − бросание двух монет. События «герб появился на первой монете» и «герб появился второй монете» − совместные.
2) Испытание − бросание монеты. События «появился герб» и «появилась цифра» − несовместные.
Определение 2. Два события A и B называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит.
Обозначение:
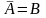 ,
,
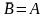 .
.
Примеры.__________________________________________________________
1)
A− выпадение герба,
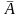 −
выпадение цифры.
−
выпадение цифры.
2) A− попадание в цель, − промах.
3) A− рождение мальчика, − рождение девочки.
Определение 3. Несколько событий образуют полную группу, если появление одного и только одного из них в результате испытания является достоверным событием.
Примеры.__________________________________________________________
1.
Пусть
 −
выпадение n очков
при бросании игральной кости. Тогда
−
выпадение n очков
при бросании игральной кости. Тогда
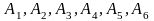 −
полная группа
событий.
−
полная группа
событий.
2. Два стрелка делают по одному выстрелу. Обозначим: попадание «+»,
промах
«−». Запишем полную группу событий:
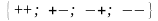 .
.
3. Противоположные события − пример полной группы событий.
Классическое определение вероятности
Несколько событий, связанных с данным испытанием называются элементарными исходами испытания, если:
1) эти события образуют полную группу, т.е. при каждом осуществлении опыта наступает одно и только одно из них;
2) эти события являются равновозможными.
Те элементарные исходы, при которых событие A наступает, называются благоприятствующими событию A.
Пример.___________________________________________________________
Испытание −
бросание игральной кости. События
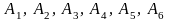 − всевозможные элементарные
исходы испытания. Пусть событие A
− на игральной кости выпало менее
пяти очков. События
− всевозможные элементарные
исходы испытания. Пусть событие A
− на игральной кости выпало менее
пяти очков. События
 −
элементарные исходы, благоприятствующие
появлению события A.
−
элементарные исходы, благоприятствующие
появлению события A.
Определение. Вероятностью события A называется отношение числа m элементарных исходов, благоприятствующих событию A, к общему числу n всевозможных элементарных исходов испытания.
Примеры_________________________________________________________
1. Испытание − бросание монеты. Событие A− выпадение герба.
Так
как n=2; m=1,
то
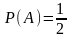 .
.
2.
Испытание − бросание игральной кости.
Событие A − на игральной
кости выпадет менее 3 очков. Это
испытание имеет следующие элементарные
исходы: {1; 2; 3; 4; 5; 6}. Из них событию A
благоприятствуют исходы {1; 2}. Поэтому
n=6, m=2.
Значит,
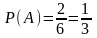 .
.
3. В урне 4 белых и 6 черных шаров. Наугад вынимают один шар.
Событие A−
этот шар белый. Так как n=10,
m=4, то P(A)= 0,4.
0,4.
Свойства вероятности.
10. Вероятность случайного события есть неотрицательное число,
заключенное
между нулем и единицей:

□ Число элементарных исходов, благоприятствующих наступлению
события,
удовлетворяет неравенству
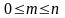 .
Поэтому
.
Поэтому
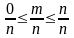 .
.
Значит,
 .
Следовательно,
■
.
Следовательно,
■
20. Вероятность достоверного события равна 1.
□ Если событие U достоверное, то ему благоприятствует любой исход
испытания, поэтому m=n. Следовательно,
 .
■
.
■
30. Вероятность невозможного события равна 0.
□ Если событие V невозможное, то ни один из исходов испытания
не благоприятствует ему. Следовательно, m=0. Тогда
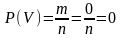 .
■
.
■
40. Сумма вероятностей противоположных событий равна 1,
т.е.

□ Если событию A благоприятствует m исходов испытания, то событию
благоприятствует n−m исходов испытания. Поэтому
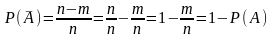 .
Значит,
.
Значит,
Если
обозначить P(A)=p,
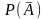 =q,
то p+q=1.
■
=q,
то p+q=1.
■
Статистическое определение вероятности.
Пусть
произведено N
испытаний, при этом событие A
наступило ровно M
раз. Отношение
 называется относительной частотой
события A и обозначается
называется относительной частотой
события A и обозначается
 .
За вероятность события A
принимается число, около которого
группируются наблюдаемые значения
относительной частоты:
.
За вероятность события A
принимается число, около которого
группируются наблюдаемые значения
относительной частоты:
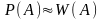 .
.
Пример.___________________________________________________________
Английский ученый Пирсон произвел 23 000 бросаний монеты. При этом герб появился 11 512 раз. Значит, относительная частота появления герба равна
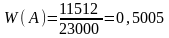 .
.
Этот пример показывает, что за вероятность появления герба можно взять число 0,5.
Основные теоремы теории вероятностей
Произведение событий
Определение 1. Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Обозначение:
С=АВ,
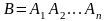 .
.
Если события A и B несовместны, то AB=V.
Пример.___________________________________________________________
Два стрелка стреляют в цель. Если
A− попадание первого стрелка, B−
попадание второго стрелка, то AB
− в цель попали оба стрелка;
 −
первый стрелок попал, а второй
промахнулся;
−
первый стрелок попал, а второй
промахнулся;
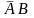 −
первый стрелок
−
первый стрелок
промахнулся, а
второй попал;
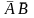 −
оба стрелка промахнулись.
−
оба стрелка промахнулись.
Зависимые и независимые события
Определение 2. Вероятность события B, вычисленная при условии, что событие A уже произошло, называется условной вероятностью события B и обозначается P(B/A).
Пример.___________________________________________________________
В урне 3 белых и 2 черных шара. Из урны дважды вынимают по одному шару, не возвращая обратно. Предположим, что при первом испытании был извлечен белый шар (событие A). Найдем вероятность появления белого шара при втором испытании (событие B). После первого испытания в урне осталось 4 шара, из них 2 белых. Значит, P(B/A)=2/4 =0,5. Если же при первом испытании был извлечен черный шар (событие C), то число белых шаров не изменилось, поэтому P(B/C)= 3/4=0,75.
Определение 3. Два события называются независимыми, если вероятность появления каждого из них не изменяется от того, появилось другое событие или нет. В противном случае события называются
зависимыми.
Если событие A не зависит от события B, то его условная вероятность равна безусловной вероятности: P(A)= P(A/B).
Определение 4. Несколько событий называются независимыми в совокупности, если вероятность появления одного из них не изменяется при появлении каких-либо других оставшихся.
Теорема умножения вероятностей
Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже произошло.
Следствие.
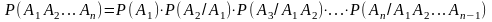
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
Следствие.

Примеры.__________________________________________________________
1. В ящике 25 деталей, из них 6 нестандартных. Найдем вероятность того, что две взятые наугад детали окажутся нестандартными.
Обозначим события: A − первая деталь окажется нестандартной, B− вторая деталь окажется нестандартной, AB − обе детали окажутся нестандартными. События A и B зависимы, поэтому
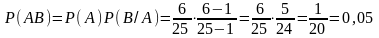 .
.
2. Произведен залп двух орудий по цели. Вероятность попадания из первого орудия (событие A) равна 0,8, из второго (событие B) − 0,75. Найдем вероятность события AB − совместного поражения цели двумя орудиями. Так как события A и B независимые, то
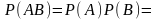 0,8∙0,75=0,6.
0,8∙0,75=0,6.
Сумма событий
Определение 5. Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Обозначение:
С=А+В,
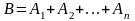 .
.
Примеры.__________________________________________________________
1. Событие «выпало не менее 5 очков» равно сумме двух несовместных событий: «выпало 5 очков» и «выпало 6 очков».
2. Два стрелка стреляют в цель. Пусть A− попадание первого стрелка, B− попадание второго стрелка. События A и B совместны, поэтому событие A+B означает, что в цель попал или первый стрелок, или второй стрелок, или попали оба стрелка.
Если рассматриваемые события несовместны, то их суммой является событие, состоящее в появлении только одного из этих событий.
Если
события
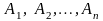 образуют полную группу, то их сумма
является достоверным событием:
образуют полную группу, то их сумма
является достоверным событием:
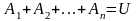 .
.
Если события A и B − противоположные, то A+B=U, AB=V.
Теорема сложения вероятностей
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Следствие
1.
 .
.
Следствие 2. Сумма вероятностей событий, образующих полную группу, равна единице.
Вероятность
суммы двух совместных событий
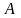 и
и
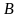 равна разности между единицей
и вероятностью произведения
противоположных событий
равна разности между единицей
и вероятностью произведения
противоположных событий
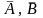 .
.
□ Событие
 состоит в появлении хотя бы одного
из событий
и
.
Противоположное ему событие
состоит в появлении хотя бы одного
из событий
и
.
Противоположное ему событие
 состоит в том, что не произойдет ни
одно из событий
и
,
т.е.
состоит в том, что не произойдет ни
одно из событий
и
,
т.е.
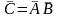 .
Так как
.
Так как
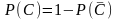 ,
то
,
то
■
Следствие
1.
 .
.
Следствие 2. Если события независимы в совокупности, то
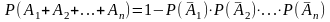 .
.
Если
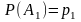 ,
,
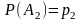 ,
…,
,
…,
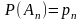 ,
то
,
то
В
частности, если
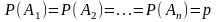 ,
то
,
то
Примеры.__________________________________________________________
1. Вероятности банкротства для двух однотипных предприятий соответственно равны 0,1 и 0,2. Найдем вероятность банкротства хотя бы одного предприятия.
Обозначим
события:
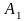 −
банкротство первого предприятия,
−
банкротство первого предприятия,
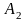 −
банкротство второго предприятия,
тогда
−
банкротство второго предприятия,
тогда
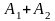 − банкротство хотя бы одного
предприятия. События
и
независимые.
− банкротство хотя бы одного
предприятия. События
и
независимые.
По
условию
 =0,1;
=0,1;
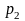 =0,2.
Значит,
=0,2.
Значит,
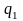 =1−0,1=0,9;
=1−0,1=0,9;
 =1−0,2=0,8.
=1−0,2=0,8.
 =1−0,9∙0,8=1−0,72=0,28.
=1−0,9∙0,8=1−0,72=0,28.
2. Вероятность попадания в цель при одном выстреле равна 0,6. Найдем вероятность хотя бы одного попадания при двух выстрелах.
Обозначим события: − попадание при первом выстреле, − попадание при втором выстреле. События и независимы.
 0,6;
0,6;
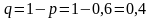 .
.
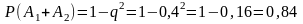 .
.