Лекции 4. Дискретные случайные величины

1. Понятие дискретной случайной величины (дсв)

Определение 1. Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно из множества возможных значений.

Определение 2. Случайная величина, принимающая различные значения, которые можно записать в виде последовательности, называется дискретной случайной величиной.

Примеры:

1) число покупателей в очереди у кассы;

2) число ДТП за сутки;

3) число бракованных изделий в партии.

Законом распределения дискретной случайной величины называется соответствие между возможными значениями случайной величины и их вероятностями.

Закон распределения дискретной случайной величины может быть задан в виде таблицы, первая строка которой содержит возможные значения , а вторая – соответствующие вероятности :

X			…
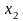
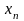
P			…

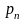
События , ,…, образуют полную группу, поэтому

.

Определение 3. Две случайные величины называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина. В противном случае случайные величины называются зависимыми.

2. Числовые характеристики дсв

1. Математическое ожидание

Определение. Математическим ожиданием дискретной случайной величины 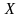называется сумма произведений значений этой случайной величины на соответствующие вероятности:

Математическое ожидание – это среднее значение данной случайной величины, центр ее распределения. Из определения следует, что M(X) − величина неслучайная, постоянная.

Пример 1._________________________________________________________

Случайная величина Х задана законом распределения

Х	1	2	3
P	0,3	0,5	0,2

Вычислим ее математическое ожидание:

M(X) = 1∙0,3+2∙0,5+3∙0,2=0,3+1+0,6=1,9.

Свойства математического ожидания

1⁰. , где C − const.

2⁰. .

3⁰. .

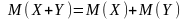Следствие: .

4⁰. , где C − const.

5⁰. , если X и Y независимы.

Пример 2 ._________________________________________________________

Найдем математическое ожидание случайной величины 5X−2Y+1 , если известно, что M(X)=2, M(Y)=3. Используя свойства математического

ожидания, получим M(5X−2Y+1)= 5M(X)−2M(Y)+1= 5∙2−2∙3+1=5.

2. Дисперсия

Определение 1. Разность называется отклонением случайной величины Х от ее математического ожидания.

Эта разность также есть случайная величина. Пусть M(X)=a. Тогда случайная величина X−a имеет закон распределения:

Х−a	−a	−a	…	−a
P			…

Теорема. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю.

Определение 2. Дисперсией случайной величины называется математическое ожидание квадрата отклонения этой случайной величины от ее математического ожидания:

.

Если случайная величина Х − дискретная, то

.

Дисперсия характеризует рассеяние возможных значений случайной величины около ее математического ожидания.

Определение 3. Средним квадратическим отклонением случайной величины называется квадратный корень из дисперсии:

.

Из определения следует, что дисперсия есть постоянная величина.

Пример 3._________________________________________________________

Используя условие примера 1, убедимся, что математическое ожидание отклонения равно нулю. Для этого составим закон распределения случайной величины Х−M(Х): из всех значений Х вычтем M(X)=1,9.

Х−M(Х)	−0,9	0,1	1,1
P	0,3	0,5	0,2

Тогда, −0,9∙0,3+0,1∙0,5+1,1∙0,2=−0,27+0,05+0,22=−0,27+0,27=0.

Вычислим дисперсию и среднее квадратическое отклонение:

D(X)=(−0,9)²∙0,3+(0,1)²∙0,5+(1,1)²∙0,2=0,243+0,005+0,242=0,49;

.

Свойства дисперсии

1⁰. 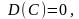где − const.

2⁰. Если − случайная величина, .

3⁰. , .

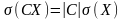4⁰. , если X и Y независимы.

Следствие: .

5⁰. .

Пример 4 ._________________________________________________________

Найдем дисперсию случайной величины 5X− 2Y+1 , если известно, что D(X)=0,2, D(Y)=1, а X и Y − независимы. Используя свойства дисперсии, получим D(5X−2Y+1)=5² ∙D(X)+2² ∙D(Y)+0=25∙0,2+4∙1=9.

Формула для вычисления дисперсии. Дисперсия случайной величины равна разности между математическим ожиданием квадрата этой величины и квадратом ее математического ожидания.

Пример 5._________________________________________________________

Найдем дисперсию случайной величины Х из примера 1 по формуле.

Математическое ожидание уже вычислено в примере 1: M(X)=1,9.

M(X²) = 1²∙0,3+2²∙0,5+3²∙0,2 = 1∙0,3+4∙0,5+9∙0,2 = 4,1.

D(X) = M(X²) − M²(X) = 4,1−1,9² = 4,1−3,61= 0,49.

Лекции 5. Основные законы распределения ДСВ