Решение.

1. Область определения функции. В аналитическом выражении функции есть математическая операция деления, поэтому необходимо исключить значения аргумента, при которых знаменатель равен нулю, т.е.

2. Проверка функции на четность или нечетность. . Следовательно, f(-x) ≠ f(x) и f(-x) ≠ - f(x), функция не является четной и не является нечетной, значит, ее график не будет иметь симметрии относительно системы координат.

3. Точки пересечения с осями координат.

х=0↔ у=0, (0, 0). График функции проходит через начало координат и других точек пересечения с осям нет.

4. Промежутки монотонности и экстремумы функции. Найдем производную функции и, приравняв ее нулю, определим критические точки. Прежде чем находить производную, преобразуем формулу данной функции к более удобному для дифференцирования виду:

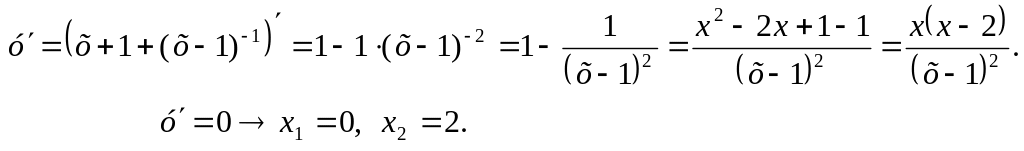
На промежутках (-∞; 0) и (2; +∞) функция возрастает, а на промежутках (0; 1) и (1; 2) – убывает, в точке х₁= 0 локальный максимум f(0)=0, в точке х₂=2 локальный минимум f(2)=4.

5. Определение точек перегиба и интервалов выпуклости и вогнутости функции. Находим вторую производную функции: .

Вторая производная не принимает значение ноль, но на промежутке (-∞; 1) она отрицательна, а значит функция выпукла, а на промежутке (1; +∞) вторая производная положительна, а значит функция – вогнута.

6. Асимптоты и поведение функции в бесконечности.

. Знак предела совпадает со знаком старшего члена функции. Прямая х=1 будет вертикальной асимптотой графика функции, причем и .

Таким образом, прямая у=х+1 будет наклонной асимптотой графика функции.

7. Просчитаем несколько дополнительных значений функции для построения графика.

х	-5	-3	-1	0	0,5	1,5	2	3	5
у	-4,1(6)	-2,25	-0,5	0	-0,5	4,5	4	4,5	6,25

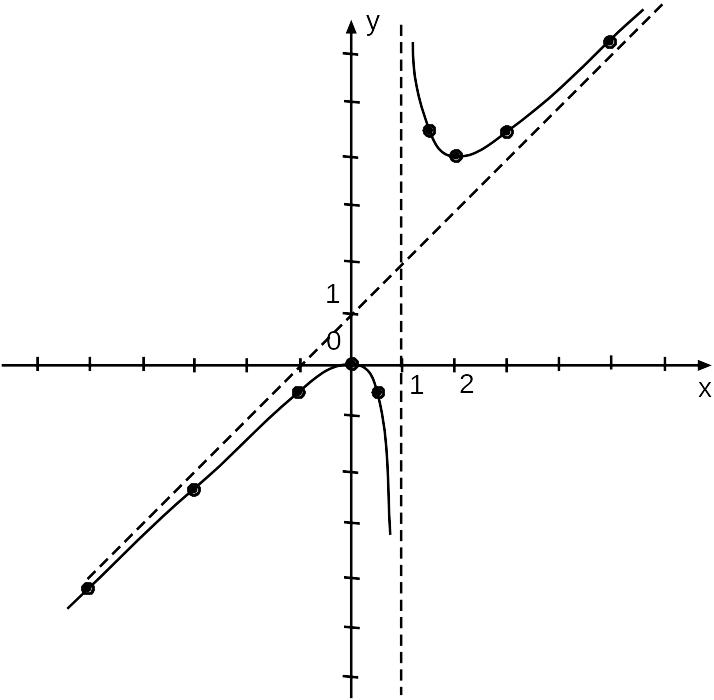
Задача 204. Исследовать математическими методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.

Решение.

1. Область определения функции.

В аналитическом выражении функции содержится вычисление натурального логарифма, поэтому на значения аргумента накладывается ограничение x>0, т.е.:

2. Проверка функции на четность или нечетность.

Исходя из односторонности области определения функции ни о четности-нечетности, ни о периодичности функции речи быть не может.

3. Точки пересечения с осями координат.

x>0, поэтому с осью Оу пересечения нет.

. Если решать это уравнение графически, то мы увидим, что график левой части не пересекается с графиком правой части. Поэтому с осью Ох пересечения тоже нет. График целиком расположен в первом координатном углу.

4. Промежутки монотонности и экстремумы функции.

Найдем производную функции: .

На промежутке (0; 1) производная отрицательная, следовательно, функция убывает, а на промежутке (1; +∞) – производная положительная, следовательно, функция возрастает, в точке х=1 локальный минимум f(1)=1.

5. Определение точек перегиба и интервалов выпуклости и вогнутости функции. Для определения точек перегиба, находим вторую производную функции:

. Вторая производная на всей области определения положительна, следовательно, функция всюду вогнута и не имеет точек перегиба.

6. Асимптоты и поведение функции в бесконечности.

, ось Оу является вертикальной асимптотой функции.

, отсюда следует, что наклонной асимптоты у графика функции нет.

7. Просчитаем несколько дополнительных значений функции для построения графика.

х	0,1	0,3	1	2	3	5
у	≈4,6	≈2,5	1	≈2,6	≈6,8	≈22

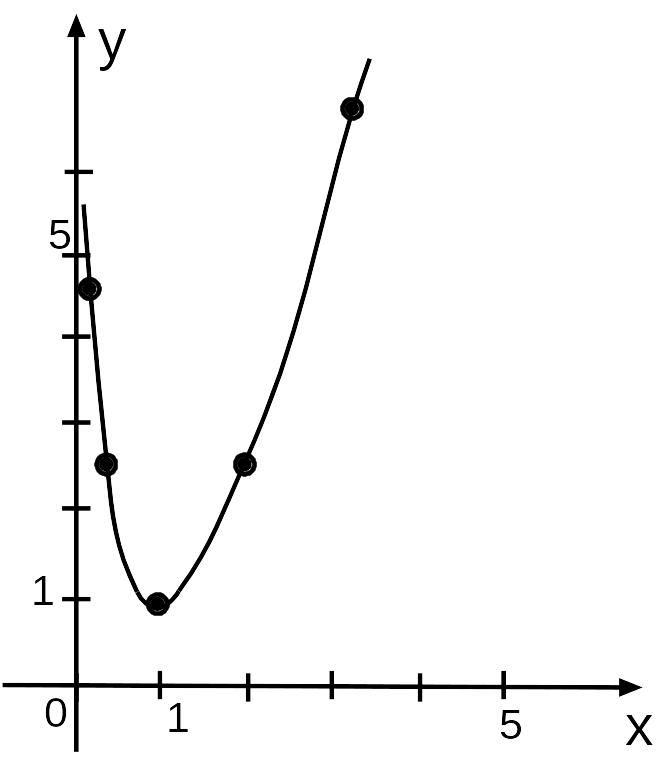
Задача 234. Дана функция . Показать, что

.