Контрольная работа
по высшей математике
Вариант 4
Задача 14. Даны координаты вершин пирамиды А1А2А3А4 –
А1(-3; 5; 4); А2(8; 7; 4); А3(5; 10; 4); А4(4; 7; 8). Найти:
1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
Решение.
А1(-3; 5; 4); А2(8; 7; 4); А3(5; 10; 4); А4(4; 7; 8).
П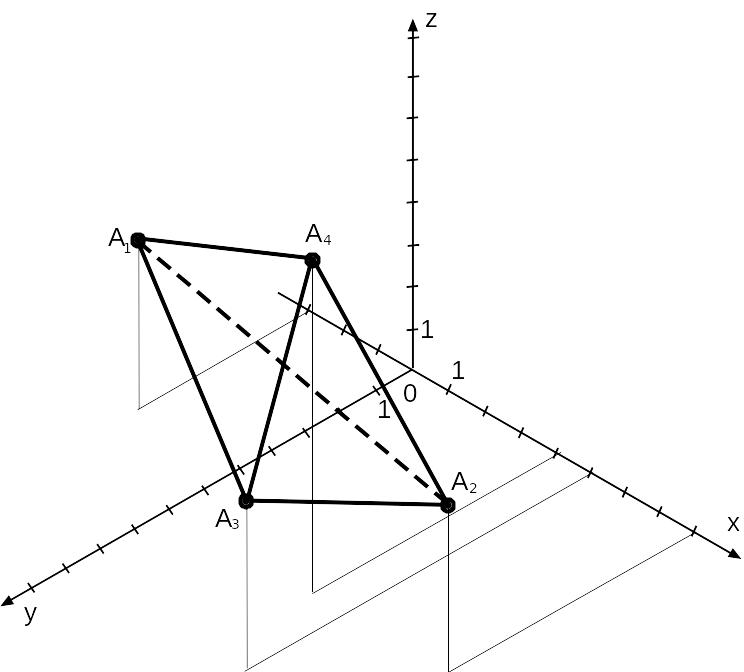
остроим
сразу чертеж пирамида в изометрической
проекции.
Задачу удобнее решать, используя методы векторной алгебры. Поэтому перейдем сразу к векторам. Если заданы две точки своими координатами А1(х1; y1; z1), А2(х2; y2; z2), то координаты соответствующего вектора находятся по формуле:
.
;
;
.
1). Длина (модуль)
вектора
обозначается
|
| и
определяется по формуле:
или
.
2). Косинус угла
между двумя векторами определяется
через скалярное произведение этих
векторов по следующей формуле. Пусть
=(х1;
y1;
z1)
и
=(х2;
y2;
z2),
тогда
α=arcos 0,8722 ≈ 29017´.
3). Перенесем это задание в конец работы, так как прежде нужно записать уравнение плоскости (п. 7) и прямой.
4). Площадь грани
А1А2А3
найдем через векторное произведение
×
,
модуль которого дает площадь
параллелограмма, построенного на этих
векторах, а половина этой площади и есть
площадь грани А1А2А3.
.
.
По координатам точек и векторов видно, что вектора и лежат в плоскости параллельной плоскости (А1А2А3), поэтому их векторным произведением будет вектор коллинеарный оси Oz.
кв. ед.
5).
Объем пирамиды
А1А2А3А4
найдем через смешанное произведение
трех векторов
,
,
по
формуле:
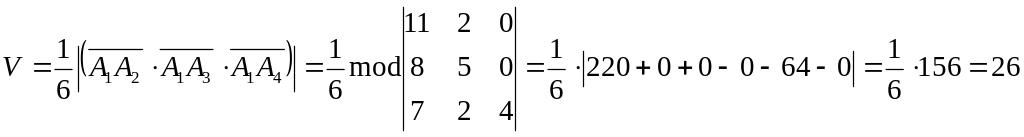куб. ед.
6). Уравнение прямой, проходящей через точки А1 и А2 с направляющим вектором запишем в параметрической форме, так как одна из координат направляющего вектора равна нулю.
Параметрические
уравнения
прямой:
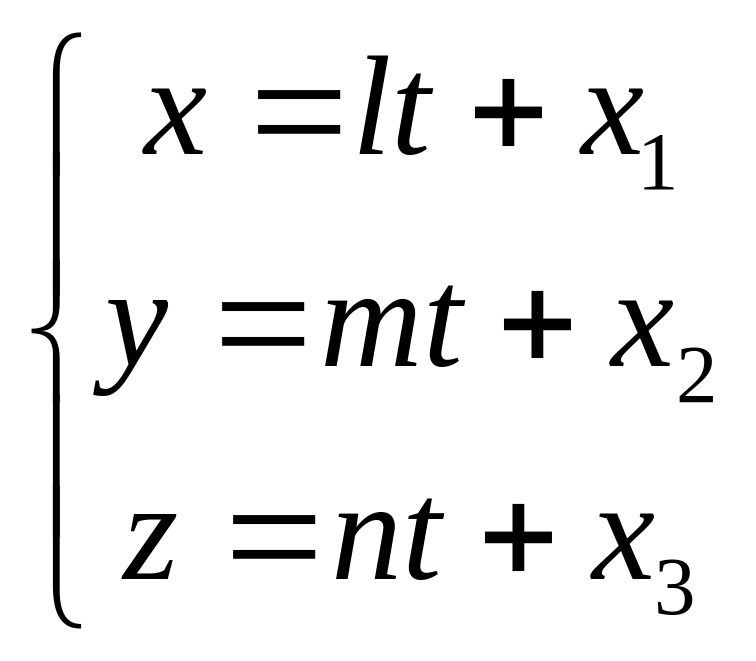определяют
прямую, проходящую через точку
А1(x1;y1;z1)
и параллельную вектору
.
Запишем уравнения прямой, проходящей через точку А1 с направляющим вектором .
(А1А2):
.
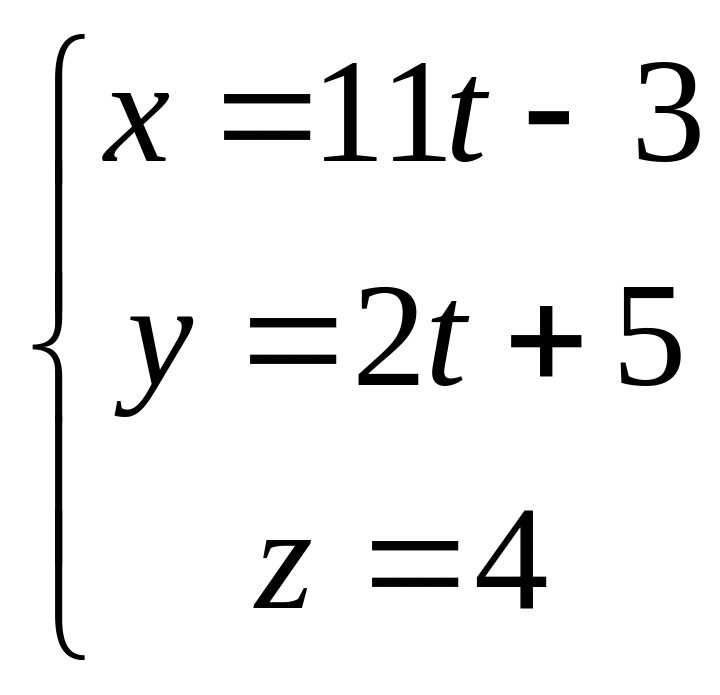7). Уравнение
плоскости (А1А2А3)
получаем их
компланарности трех векторов
,
,
,
где M(x;
y;
z)
– некоторая точка этой плоскости:
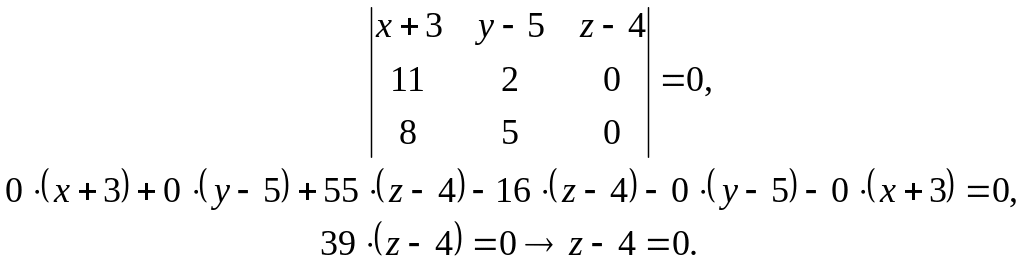
Этого следовало ожидать, так как у всех трех точек А1, А2, А3 одинаковая третья координата z=4.
8). Уравнение высоты,
опущенной из вершины А4
на грань А1А2А3
запишем, зная координаты точки А4(4;
7; 8) , через которую данная прямая проходит,
и координаты направляющего вектора,
которым в данном случае будет вектор
нормали к плоскости (А1А2А3),
равный
.
Таким образом, параметрические
уравнения
высоты, опущенной из вершины А4
на грань А1А2А3
имеет вид:
.
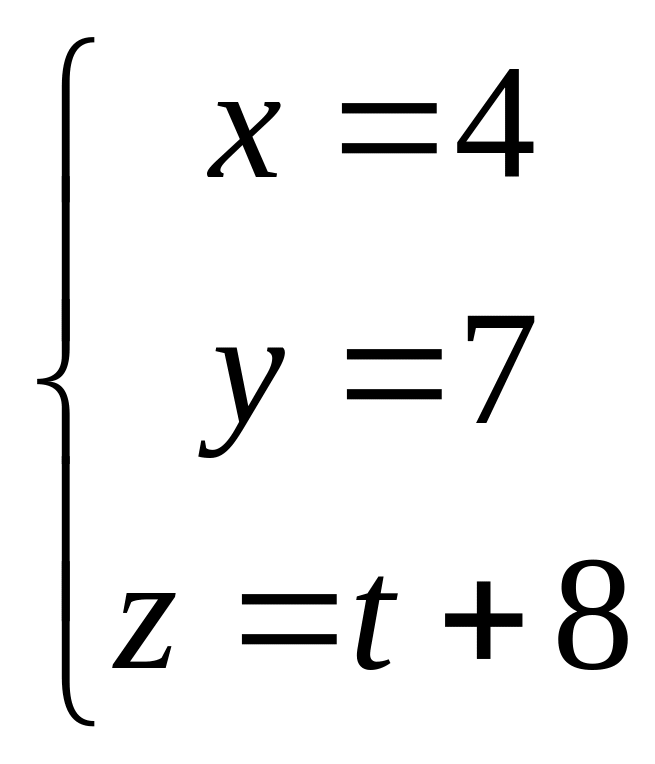3). Теперь можно
вернуться к этому заданию. Плоскость
(А1А2А3):
,
прямая
(А1А4):
,
тогда синус
угла между прямой, заданной направляющим
вектором и плоскостью, заданной вектором
нормали к плоскости, определяется
формулой:
.
φ=arcsin( 0,481543) ≈ 280 47´.
Ответы: 1).
;
2). α=arcos
0,8722 ≈ 29017´;
3).
φ=arcsin(
0,481543) ≈ 280
47´; 4).
кв.
ед.;
5).
куб. ед.; 6).
(А1А2):
;
7).
;
8).
.
Задача 54. Дана система линейных уравнений
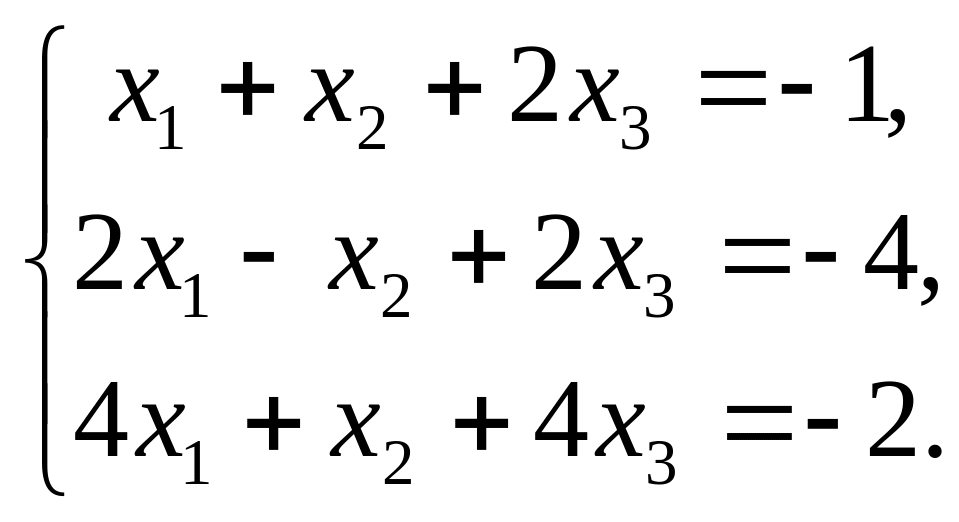
Доказать ее совместность и решить двумя способами:
1) методом Гаусса; 2) средствами матричного исчисления.
Решение.
Вычислим определитель матрицы системы по правилу треугольников:
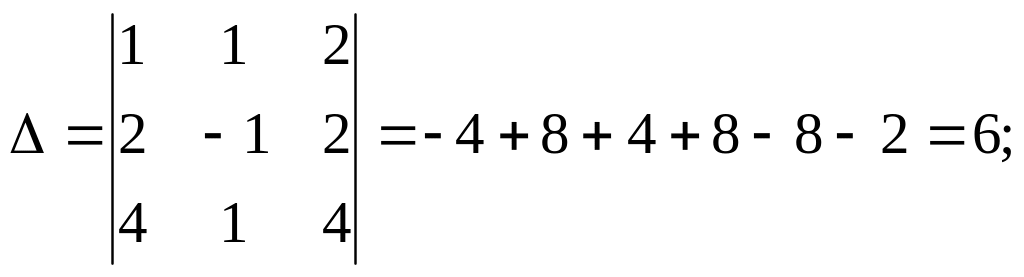
∆=6≠0, значит, система совместна, то есть имеет решение.
1). Метод Гаусса еще называют методом последовательного исключения неизвестных. В данном случае, выпишем расширенную матрицу системы, и будем работать с ней.
В качестве разрешающего элемента берем первый элемент первой строки. Первую строчку, умножив на -2 и -4 соответственно, последовательно прибавляем ко второй строке и к третьей строке. Тем самым мы исключим первую неизвестную величину из второго и третьего уравнений. Теперь разрешающим будет второй элемент второй строки. Вторую строку умножаем на -1, после этого, прибавляем к третьей строке и исключаем вторую неизвестную величину из третьего уравнения. Далее производим «обратный ход», перейдя снова к уравнениям: последовательно, начиная с третьего уравнения к первому, вычисляем неизвестные.
.
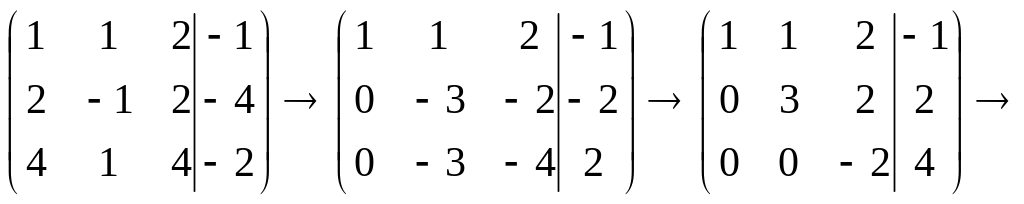
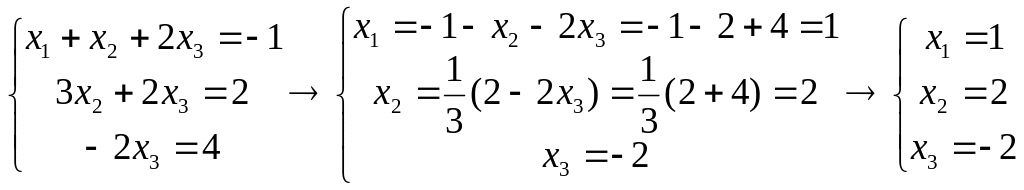2). Решение уравнения в матричной форме имеет вид:
А-1∙А∙Х=А-1∙В или Е∙Х=А-1∙В или Х=А-1∙В.
Для решения системы уравнений этим методом нужно найти матрицу обратную к матрице системы (это возможно, т. к. матрица системы невырожденная) и умножить ее на матрицу-столбец свободных членов, получим матрицу-столбец значений неизвестных. Обратная матрица вычисляется по формуле:
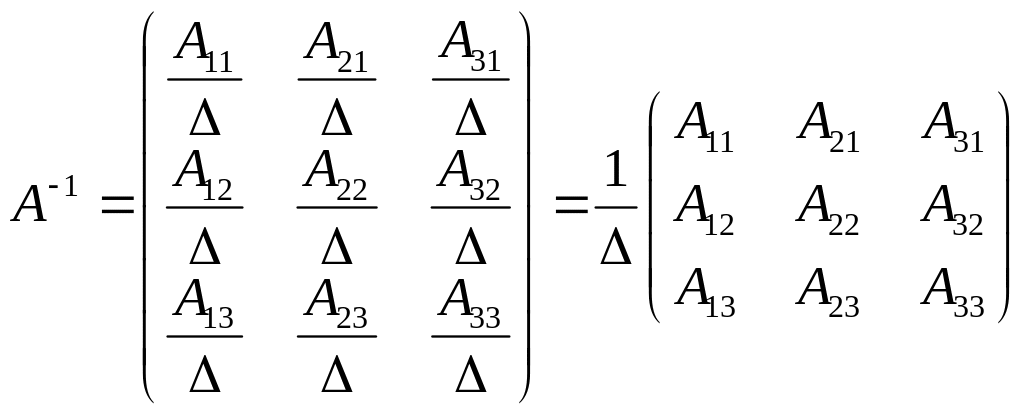
где Amn - алгебраическое дополнение элемента матрицы amn в ее определителе, т.е. произведение минора второго порядка, полученного вычеркиванием m–й строки и n–го столбца в определителе матрицы А на (-1)m+n.
, 
,
, 
,
, 
,
,
,
,
.
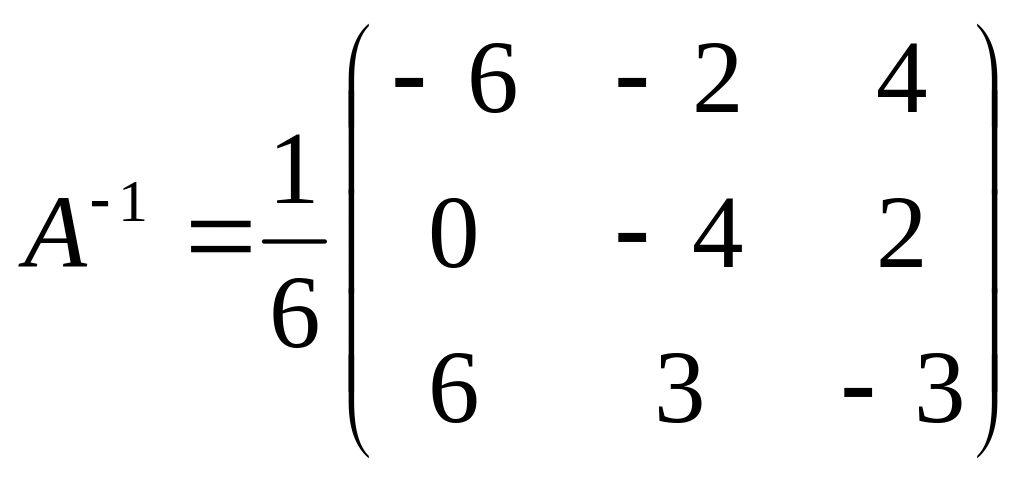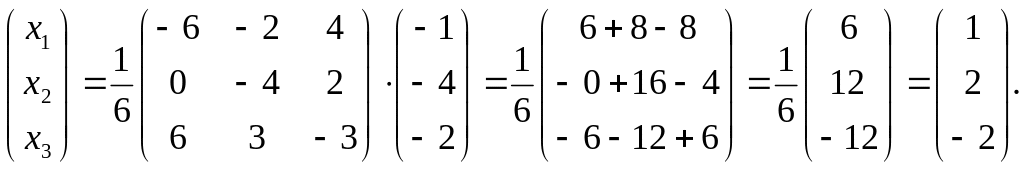
Ответ: x1=1; х2=2; х3=-2.
Задача 64. Даны два линейных преобразования:
.
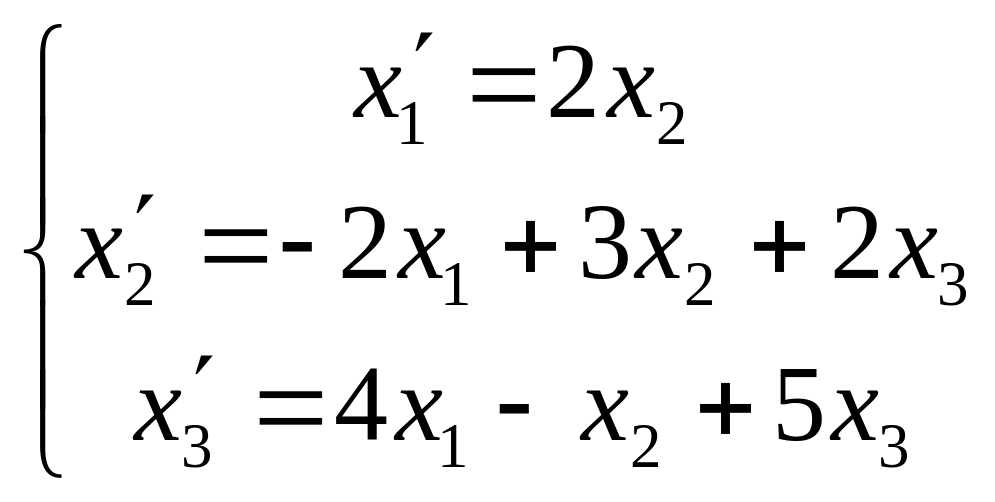
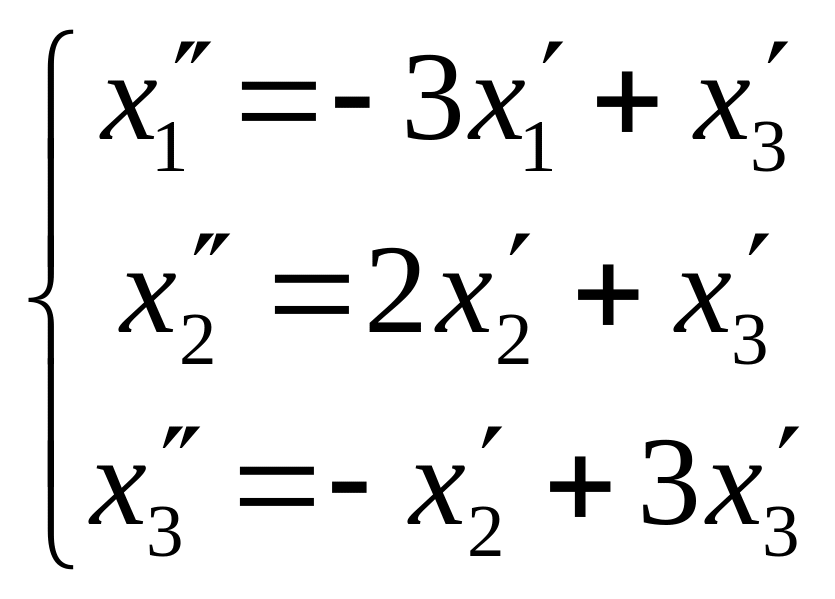Средствами
матричного исчисления найти преобразование,
выражающее
через
.
Решение.
Перепишем обе системы в матричном виде
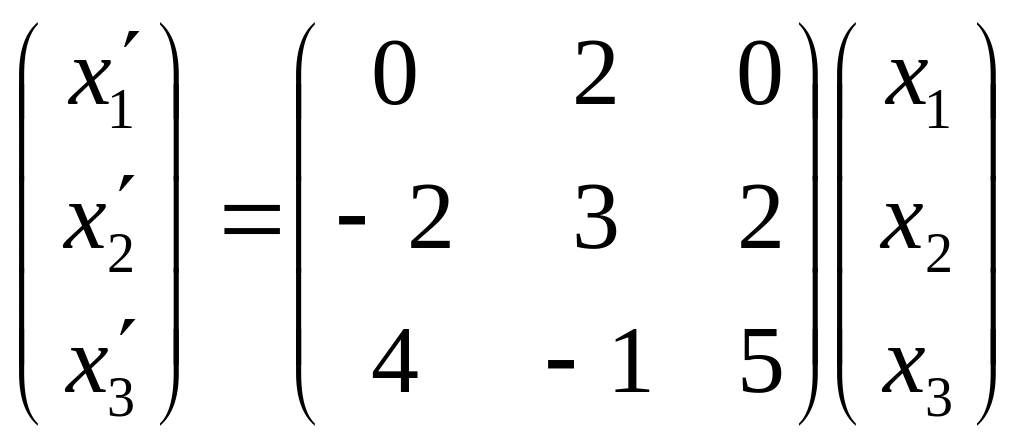и
.
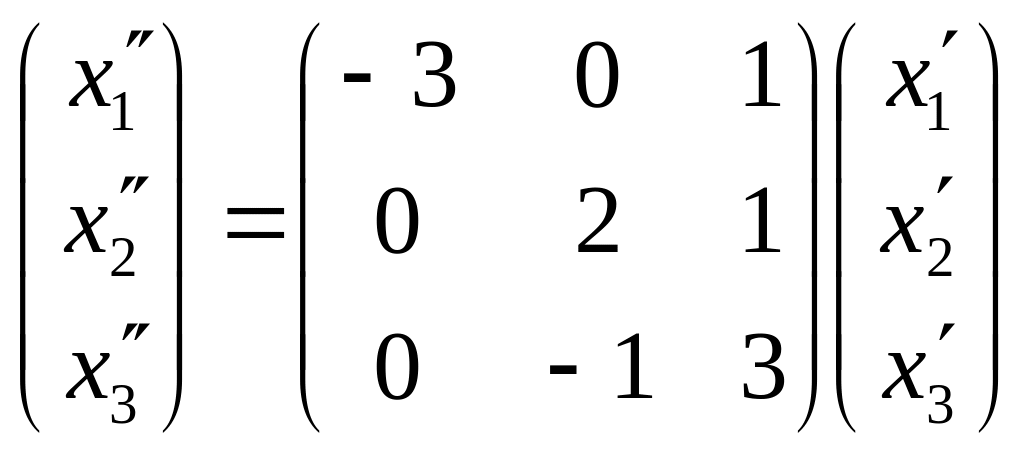Тогда искомое преобразование получается следующим образом: подстановкой и перемножением матриц преобразований:
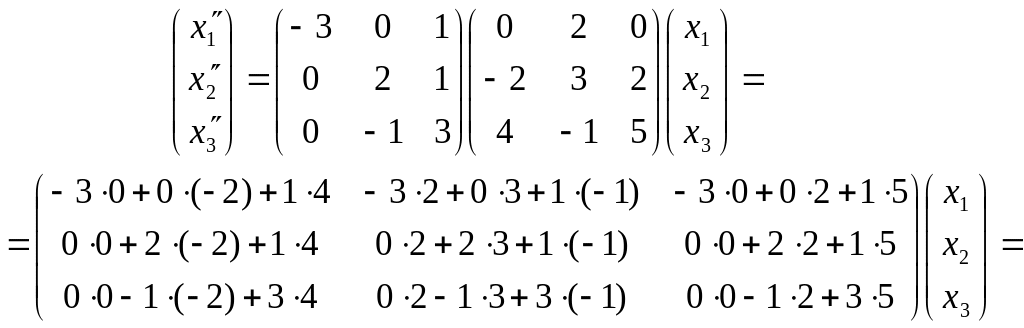
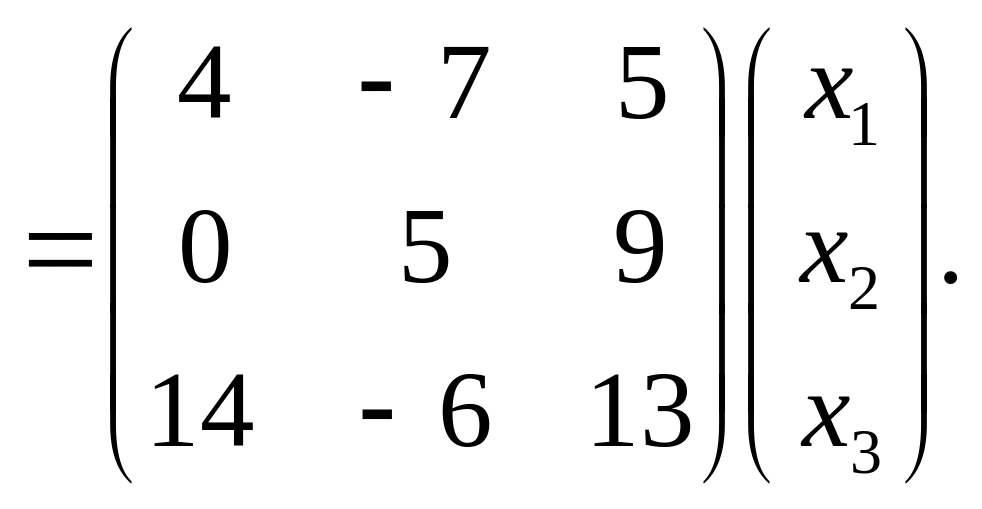
Переходя обратно к записи в виде системы, запишем ответ.
Ответ:
.
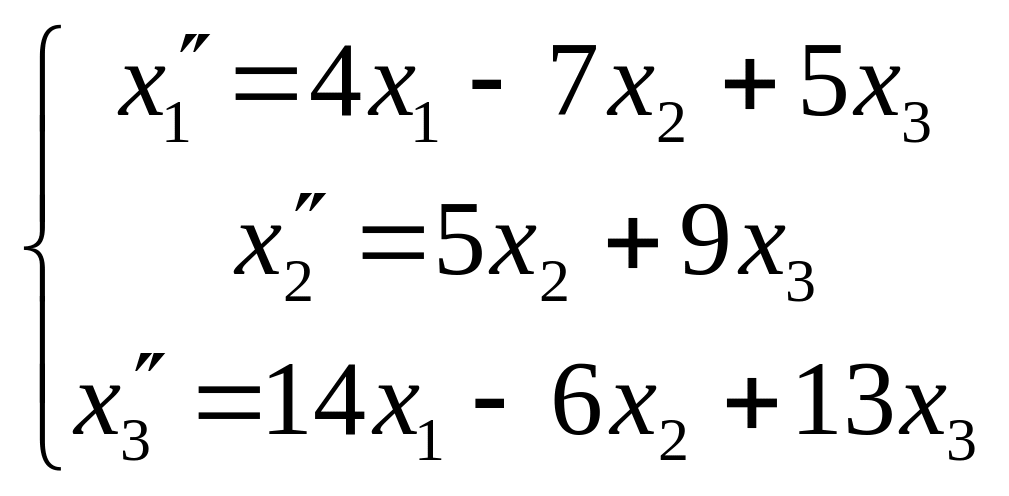Задача 114. Найти пределы функций, не пользуясь правилом Лопиталя:
а)
;
б)
;
в)
;
г)
.
Решение.
а). При непосредственной
подстановке получается неопределенность
,
поэтому числитель и знаменатель поделим
одновременно на высшую степень аргумента
х4,
тогда в полученном выражении
,
,
,
при х→∞.
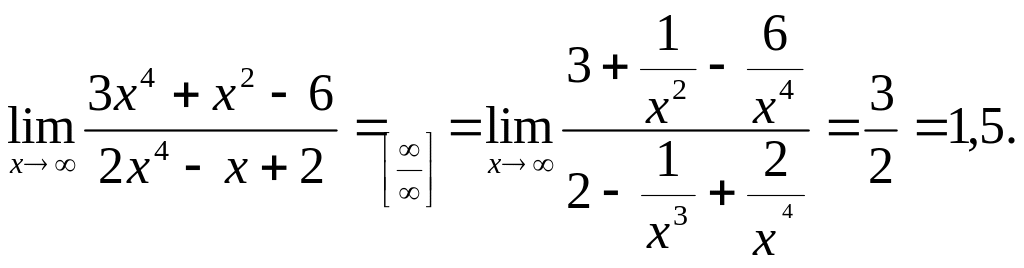
б). При непосредственной
подстановке получается неопределенность
,
поэтому предварительно умножим числитель
и знаменатель одновременно на выражение
сопряженное знаменателю, тогда в
знаменателе получим разность квадратов,
после чего дробь можно будет сократить
и предел вычисляется.
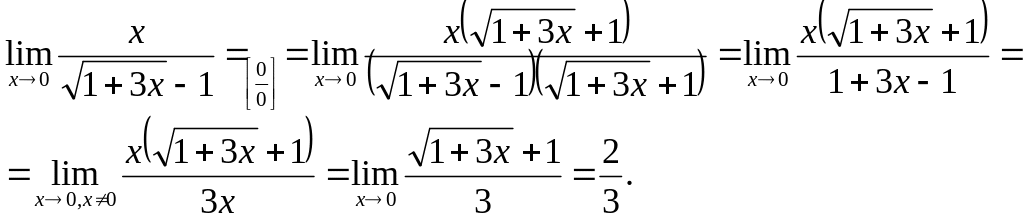
в). При непосредственной
подстановке получается неопределенность
,
поэтому предварительно введем подстановку:
полагая arctgx=y,
имеем
.
Остается найти предел
При нахождении
которого, использовали первый замечательный
предел
.
г). При непосредственной
подстановке получается неопределенность
,
поэтому постараемся свести ко второму
замечательному пределу.
Если
и
,
то полагая φ(х)=1+α(х),
где α(х)→0
при х→0
и, следовательно,
,
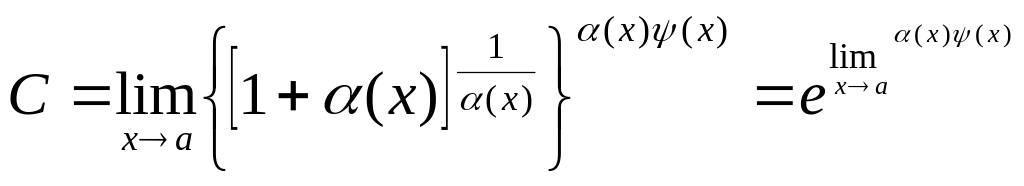где е
≈ 2,718…
.
Ответы: а).
1,5; б).
;
в). 5 ; г). е2.
Задача 134. Задана
функция
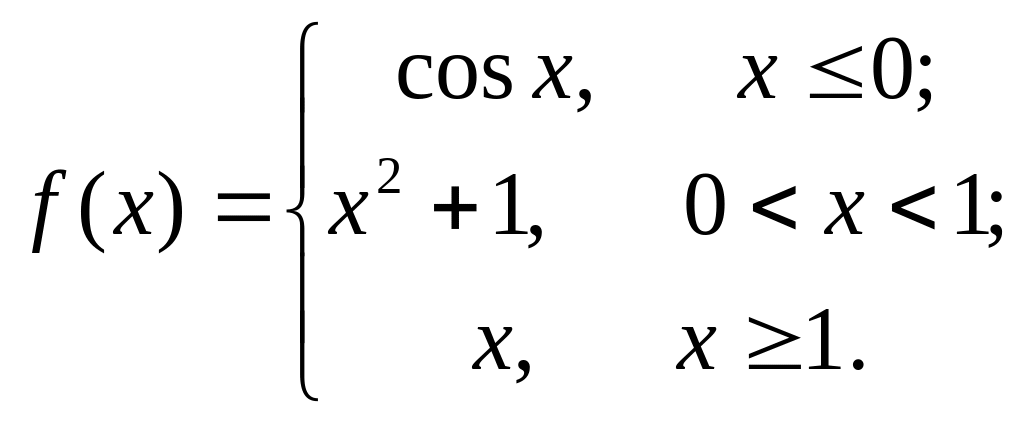Найти точки разрыва функции, если они
существуют. Сделать чертеж.