6. Арифметические свойства сходящихся последовательностей.

7. Предельный переход в неравенствах (для последовательностей).

8. Монотонные последовательности. Теорема о пределе монотонной последовательности.

9. Применение теоремы о пределе монотонной последовательности к вычислению пределов.

10. Число e.

«Существует ли предел последовательности , и если существует, то чему равен этот предел»? Для того, чтобы дать ответ нам этот вопрос понадобится следующая лемма:

Лемма 1. Для любого и любого справедливо неравенство (1) Д о к а з а т е л ь с т в о. Проведем его по индукции. При n = 1 неравенство (1), очевидно, выполняется как равенство (вообще при любом ). Предположим, что оно справедливо при n = k, т.е. предположим, что . Тогда , т.е. оно справедливо и при n = k + 1. Таким образом, в соответствии с методом математической индукции неравенство (1) верно _. 

Замечание 1. Обратите внимание на то, где мы при доказательстве воспользовались условием, что .

Лемма 2. Существует предел .

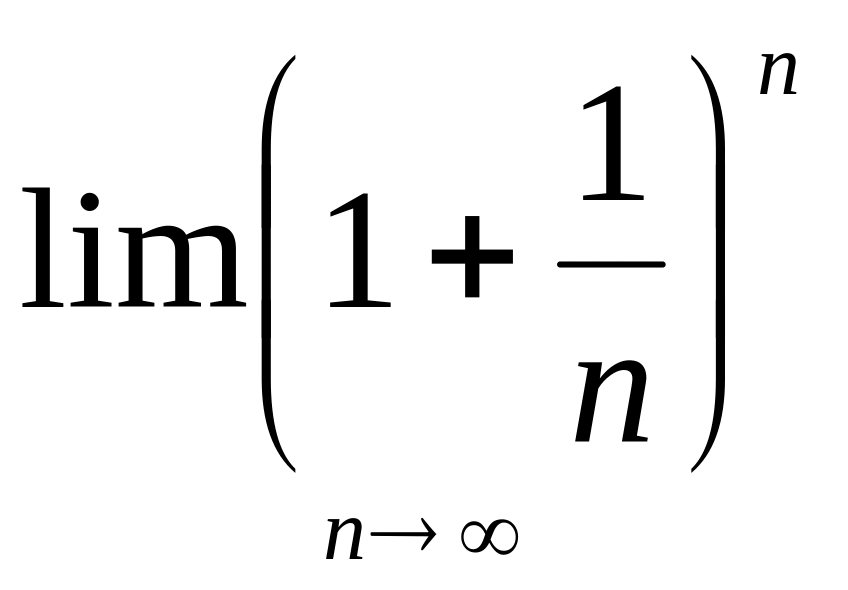Д о к а з а т е л ь с т в о. Рассмотрим сначала последовательность , Используя неравенство Бернулли, при будем иметь:

Таким образом, и следовательно , то есть последовательность - убывающая.

Кроме того, очевидно, что последовательность положительная . Следовательно, она ограничена снизу. Поэтому существует предел Возвращаясь к интересующей нас последовательности , , видим, что . Поскольку существуют пределы: и , то по теореме о пределе произведения последовательностей существует и предел _{т.е. предел} ■

Замечание 2. Этот предел обозначают буквой e и называют числом e. Можно доказать, что число e иррациональное. В настоящее время оно вычислено с большей степени точности в частности, в пределах первых пятнадцати знаков после запятой

e = 2,718281828459045…

11. Бесконечно малые и бесконечно большие последовательности.

Последовательность называется бесконечно малой (б.м.), если .

Замечание 1. Очевидно, что если , то , (т.е. - б. м. последовательность) при этом .

Наоборот, если имеет место это равенство и - б. м. последовательность, то .

Таким образом, последовательность имеет предел тогда и только тогда, когда она равна сумме постоянной и бесконечно малой последовательностей.

Теорема 1. Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.

Определение 2. Если для любого вещественного числа E N: x_n > E n > N (соотв., x_n < E n > N ), то говорят, что последовательность имеет своим пределом , и пишут или .

Определение 3. Последовательность такую, что , называют бесконечно большой и пишут (символ  употребляется без знака).

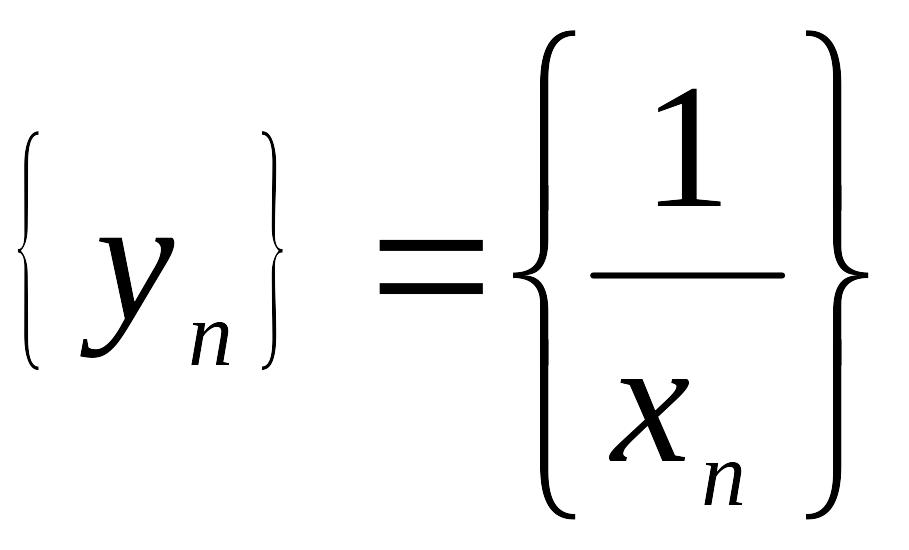Теорема 2. Если последовательность - бесконечно большая и то - бесконечно малая последовательность.

Теорема 3. Если - бесконечно малая последовательность и при n = 1,2,…, то последовательность -бесконечно большая.

Замечание 2. Последовательности, имеющие своим пределом + или - мы не относим к сходящимся, то есть они считаются расходящимися. Таким образом, можно сказать, что сходящиеся последовательности – это такие последовательности, которые имеют конечный предел.

Замечание 3. Последовательности, имеющие пределы + или -, очевидно, являются бесконечно большими. Однако не всякая бесконечно большая последовательность имеет предел равный + или -. Например, последовательность очевидно является бесконечно большой ( ), но она не имеет ни конечного, ни какого-то бесконечного () предела.