
- •Основные понятия и определения тоау. Состав асу. Структура асу. Основные принципы разработки асу.
- •Особенности функционирования асу с человеком оператором.
- •Постановка задач управления динамическими системами.
- •Задача стабилизации. Линейные динамические системы.
- •Подобные преобразования линейных динамических систем.
- •Управляемость динамических систем.
- •Наблюдаемость динамических систем.
- •Устойчивость решений динамических систем. Знакопостоянные и знакоопределенные функции.
- •Прямой (второй) метод исследования устойчивости Ляпунова.
- •Первый метод Ляпунова исследования устойчивости динамических систем.
- •Принцип оптимальности Беллмана для задачи быстродействия.
- •Принцип оптимальности Беллмана для неотрицательного функционала (критерия оптимальности).
- •Принцип оптимальности Беллмана для линейных динамических систем.
- •Связь метода динамического программирования с методом Ляпунова.
- •Выбор критерия оптимальности при оптимальном управлении линейными динамическими системами.
- •Главные малые колебания динамической системы. Управляемость и наблюдаемость колебательных систем.
- •Идентификация статических математических моделей при разработке систем управления.
- •Планы первого и второго порядка. Критерии оптимальности планов.
- •Идентификация динамических математических моделей.
- •Последовательный (итерационный) метод наименьших квадратов при идентификации математических моделей.
- •Дискретные системы управления. Z – преобразование для линейных дискретных систем.
- •Свойства z – преобразования.
- •Решение разностных уравнений.
- •Обратное z – преобразование.
- •Передаточные функции разомкнутых импульсных систем.
- •Передаточные функции замкнутых импульсных систем.
- •Метод корневого годографа для непрерывных и дискретных систем управления.
- •Билинейное преобразование
- •Оценка точности в установившимся режиме для цифровых су.
- •Использование корректирующих устройств для улучшения характеристик су
- •Пид регуляторы и их передаточные функции.
- •Идентификация динамических моделей с помощью анализа переходных характеристик. Общая характеристика методов.
- •И дентификация динамических моделей с помощью анализа переходной ступенчатой характеристики.
- •Идентификация динамических моделей с помощью анализа переходной импульсной характеристики.
- •Идентификация динамических моделей с помощью анализа амплитудной и фазовой характеристик.
- •Идентификация динамических моделей с помощью метода корреляционных функций.
Главные малые колебания динамической системы. Управляемость и наблюдаемость колебательных систем.
Рассмотрим
линейную колебательную динамическую
систему с управлением
![]() ,
(5.22) где
,
(5.22) где
![]() и
- квадратные матрицы размерностью
,
и
- квадратные матрицы размерностью
,
![]() - вектор управления,
- матрица коэффициентов управления,
размерностью
- вектор управления,
- матрица коэффициентов управления,
размерностью
![]() .
.
Для
определения управляемости и наблюдаемости
системы (5.22) необходимо также как для
произвольной линейной системы перейти
к главным или нормальным координатам.
Главные координаты линейной системы
х*
характеризуются тем, что при переходе
к ним все дифференциальные уравнения
в системе (5.16) полностью отделяются друг
от друга, если рассматривается система
(5.22) без управления (u
= 0). В главных координатах система (5.22)
принимает вид
![]() (5.23), где
(5.23), где
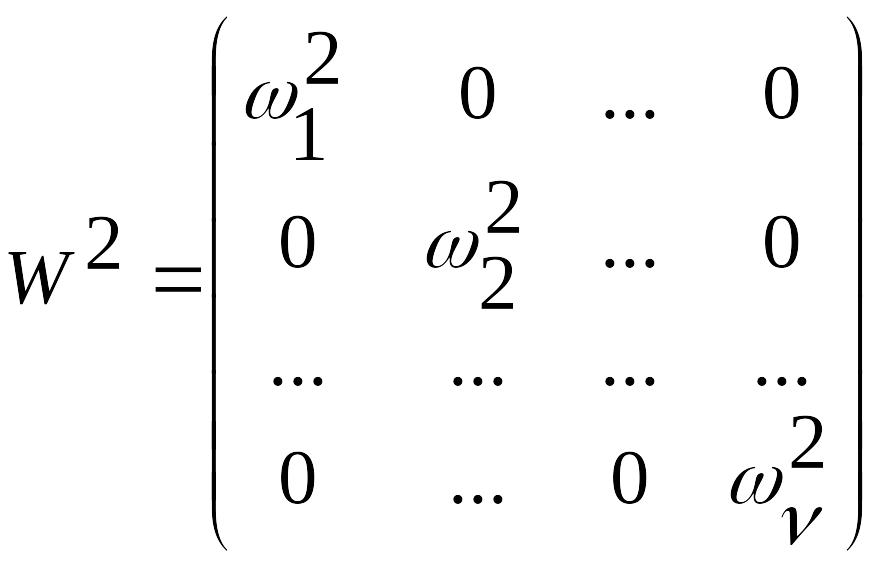 - диагональная матрица.
- диагональная матрица.
Все
уравнения системы (5.23) легко интегрируются
и имеют решение вида
![]() (5.24), где
;
(5.24), где
;
![]() - произвольные постоянные.
- произвольные постоянные.
Теперь, если ввести матрицу V = (V ( j )), составленную из собственных векторов системы, и сравнить решения в обычных (5.21) и в главных (5.24) координатах, нетрудно найти связь между этими координатами x = Vx* (5.25).
Определим
управляемость линейной колебательной
системы, используя тот же метод, что и
для произвольной линейной системы.
Подставив замену переменных (5.25) в
систему с управлением и умножив слева
на обратную матрицу V–1a–1,
получим
![]() (5.26), где
(5.26), где
![]() ,
,
![]() .
Причем последнее соотношение может
служить проверочным при преобразовании
к главным координатам.
.
Причем последнее соотношение может
служить проверочным при преобразовании
к главным координатам.
В соответствии с критерием Гильберта линейная система (5.26), приведенная к главным координатам, управляема, если ни одна из строк матрицы не является нулевой (то есть для управляемости в каждой строке матрицы m* должен быть по крайней мере один ненулевой элемент). Если матрица m* представляет собой матрицу-столбец (это будет тогда, когда управление u - скалярная величина), то критерий управляемости требует, чтобы ни одна компонента этого столбца не была нулевой.
Замечание.
Система с управлением (5.26) распадается
на
уравнений вида
![]() (5.27), где
(5.27), где
![]() -
-
![]() -ая
строка матрицы m*.
Это уравнение при отличии от нуля хотя
бы одной компоненты строки
управляема.
-ая
строка матрицы m*.
Это уравнение при отличии от нуля хотя
бы одной компоненты строки
управляема.
Получим критерий наблюдаемости для линейных колебательных динамических систем вида (5.22). Исходную систему уравнений (5.22) рассмотрим совместно с математической моделью измерительного устройства z = Cx (5.28), где матрица C определяет линейную связь между вектором состояния системы x и вектором измеряемых переменных z.
Для
того, чтобы определить наблюдаемость
колебательной системы (5.22) необходимо
перейти к главным координатам (5.25), тогда
![]() (5.29).
(5.29).
Таким образом, критерий наблюдаемости для системы (5.22) формулируется следующим образом: система наблюдаема, если ни один из столбцов матрицы C* = CV не является нулевым.
Действие на колебательную систему возмущений. Метод малого параметра.
Метод Ван-дер-Поля. Качественное исследование усредненной системы.
Метод усреднения для системы с двумя быстрыми фазами.
Применение метода усреднения для исследования колебательной системы с двумя степенями свободы.
Оптимальное управление колебаниями с одной степенью свободы.
Оптимальное управление колебаниями с двумя степенями свободы.
Теорема Боголюбова Н.Н. о близости решений исходной и усредненной систем уравнений. Системы стандартного вида. – не нужно!
