12. Принцип оптимальности Беллмана для неотрицательного функционала (критерия оптимальности).

Принцип оптимальности Беллмана: «Оптимальные стратегии управления обладают тем свойством, что каково бы ни было начальное состояние системы и управление в начальный момент, последующее управление должно быть оптимальным в смысле заданного критерия относительно любого другого состояния, которое могло бы явиться естественным следствием управления в начальный момент». Этот принцип для динамических систем может быть сформулирован короче: любой отрезок оптимальной траектории есть тоже оптимальная траектория.

Критерий оптимальности имеет вид 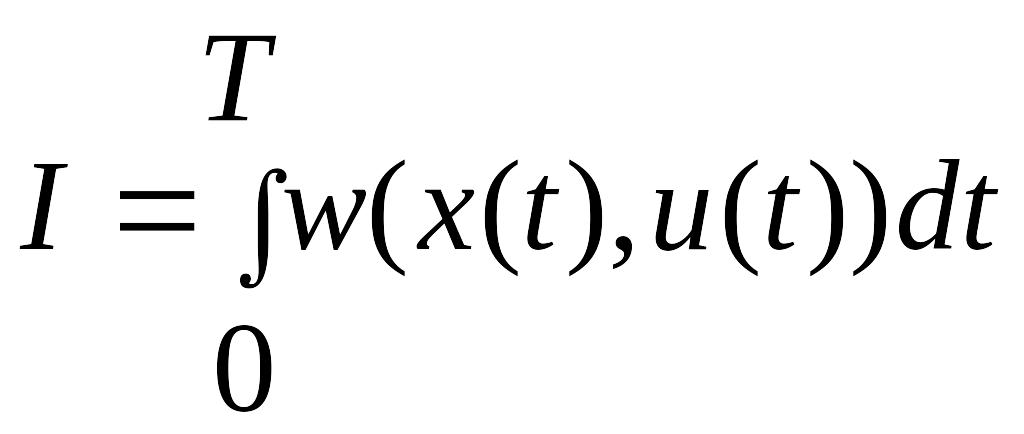(3.4), где функция является положительно определенной квадратичной формой векторов x, u. При этом функция обращается в ноль только при x = u = 0. В частности, этому условию удовлетворяет функционал линейной системы . Введем новое время

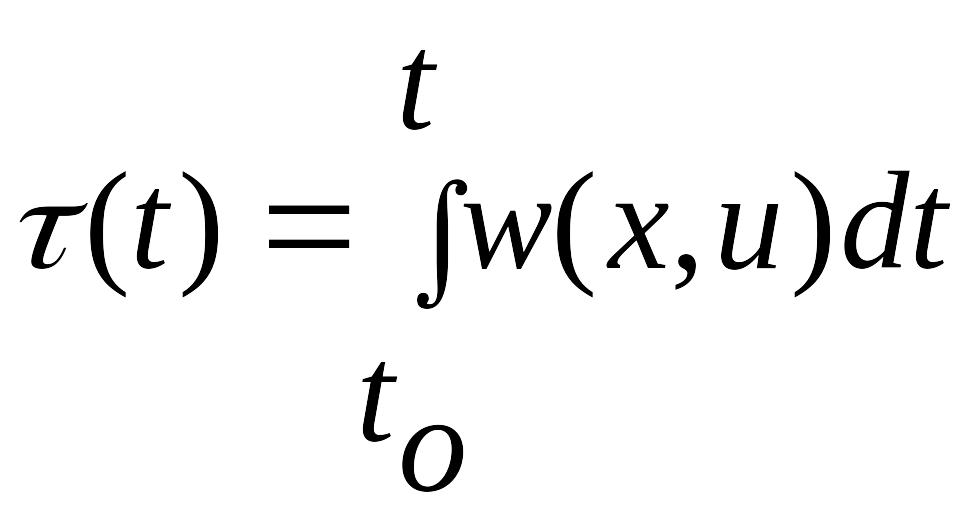(3.5), где в силу автономности системы можно положить t_o = 0.

Тогда, дифференцируя соотношение (3.5) по времени, получим дифференциальное уравнение для нового времени (3.6). Переходя в системе к интегрированию по новому времени , получим (3.7). В этом случае критерий оптимальности примет вид (3.8), где - конечное время.

Следовательно, приходим к той же задаче быстродействия, только с другим временем . Здесь предполагается, что допустимые траектории системы (3.7) не проходят через точку x=u=0. Исключение может составлять лишь конечная точка траектории (при t = T). Тогда, применяя ту же схему вывода уравнения Беллмана, как для задачи быстродействия, получим

или (3.9).

13. Принцип оптимальности Беллмана для линейных динамических систем.

Принцип оптимальности Беллмана: «Оптимальные стратегии управления обладают тем свойством, что каково бы ни было начальное состояние системы и управление в начальный момент, последующее управление должно быть оптимальным в смысле заданного критерия относительно любого другого состояния, которое могло бы явиться естественным следствием управления в начальный момент». Этот принцип для динамических систем может быть сформулирован короче: любой отрезок оптимальной траектории есть тоже оптимальная траектория.

Рассмотрим определение оптимального управления линейной динамической системой вида dy/dt = By + mu (3.11) при решении задачи стабилизации с квадратичным критерием оптимальности (3.12). Здесь квадратная матрица a удовлетворяет условиям Сильвестра, c > 0 - некоторая константа, T≤∞ - конечное время, u - управление (скаляр), (*) - знак транспонирования, y* - матрица-строка. В системе (3.11) матрица B и вектор m считаются заданными (в общем случае они могут зависеть от времени t).

Ставится задача об оптимальном переводе системы (3.11) из начального положения y(t_o) в начало координат y(T)=0. Для решения этой задачи используется принцип Беллмана , который для линейной системы (3.11) и критерия (3.12) приводит к соотношению (3.13). Выражение, стоящее под знаком минимума в соотношении (3.13), представляет собой квадратичную функцию управления u. Выделяя слагаемые, зависящие только от управления, получим 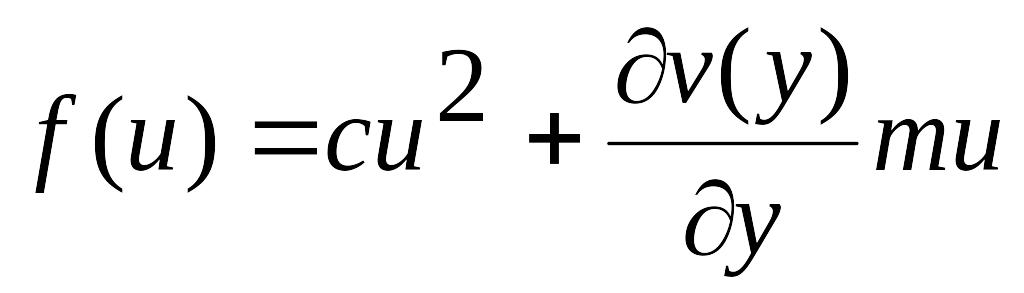. Необходимое условие минимума этой функции по управлению будет иметь вид 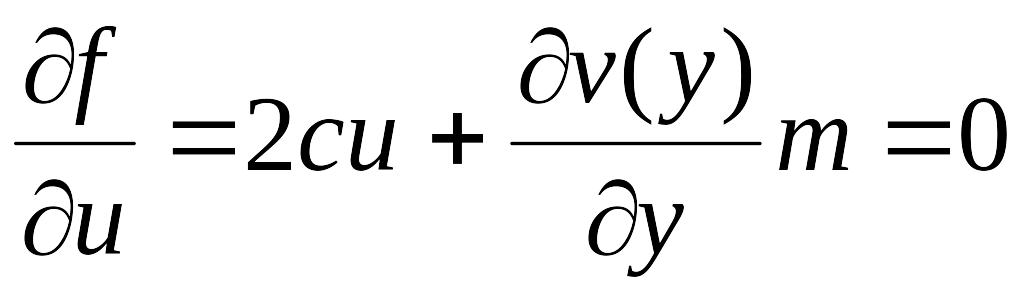(3.14). Причем выполняется достаточное условие минимума 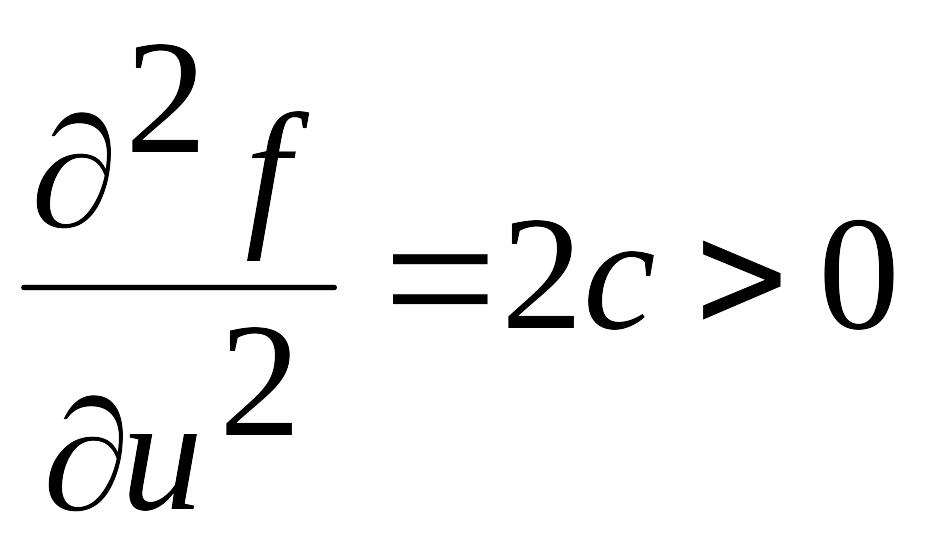. Поэтому оптимальное управление определится из условия (3.14) в виде 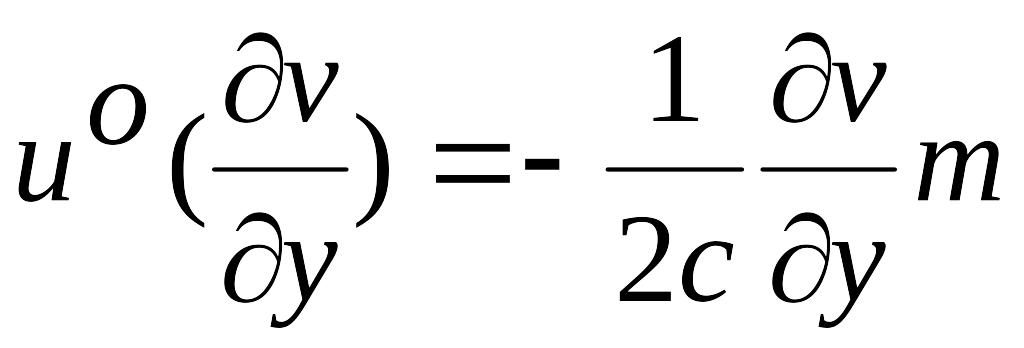(3.15), где выражение рассматривается как скалярное произведение векторов и , то есть .

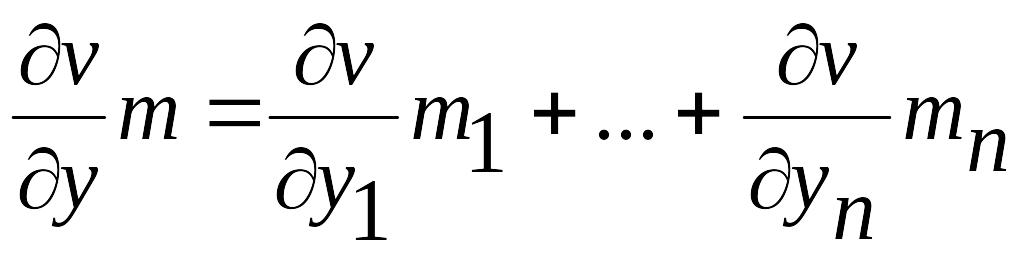Подставляя управление (3.15) в условие (3.13) и приводя подобные члены, получим уравнение Беллмана для ЛДС (3.11): 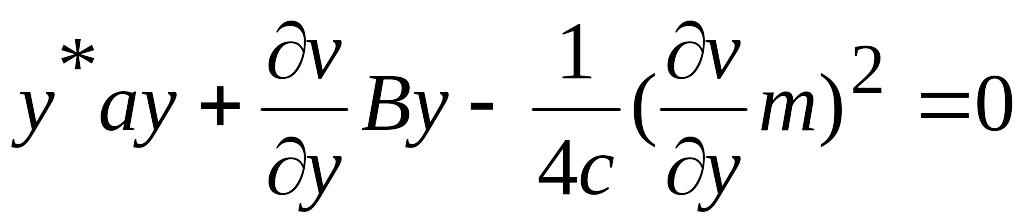(3.16).

В этом случае определение оптимального управления для линейной системы осуществляется следующим образом: 1) из уравнения в частных производных (3.16) находится функция ; 2) функция подставляется в выражение (3.15) и определяется оптимальное управление u^o(y,t). После подстановки решения полученной замкнутой системы должны удовлетворять некоторым условиям устойчивости, в частности, они должны стремится с течением времени к началу координат y(T)=0. Уравнение Беллмана (3.16) может иметь несколько решений , из которых нужно выбрать такое, которое будет обеспечивать условие устойчивости.