53. И дентификация динамических моделей с помощью анализа переходной ступенчатой характеристики.

Y(S)/ X(S)=G_p(S) – объект управления

выходной сигнал: Y(S)=G_p(S)*X(S)

Преобразование Лапласа: L{1}=1/S

, Y(S)=G_p(S)/S

- переходная ступенчатая характеристика

Пример 1:

Система 1-го порядка

, Т – постоянная времени Т -?

Нужно разложить на пустые дроби и найти соответствующие значения по таблице

а) t=T

б )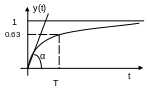

Пример 2:

Система 2-го порядка

Структура передающей функции ; ν,ω₀ – определяемые параметры

Рассмотрим случай, когда полюса комплексно сопряженные, тогда переходная характеристика имеет колебательный характер.

S₁,S₂ - комплексно сопряженные.

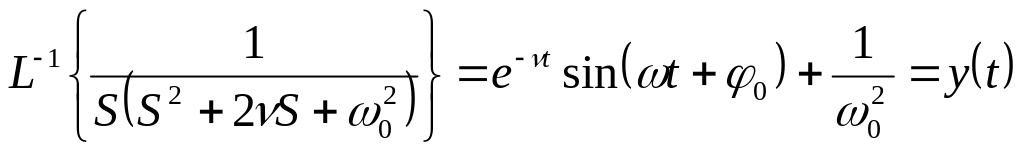- переходная характеристика

ω – частота выходного сигнала

ω₀ – частота (ν=0)

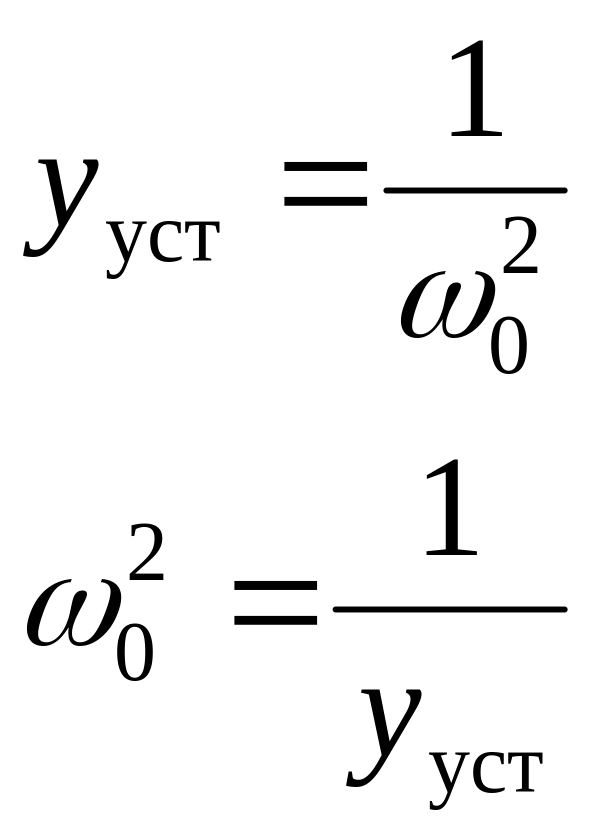
Переходим к исходному усреднению:

54. Идентификация динамических моделей с помощью анализа переходной импульсной характеристики.

Y(S)=G_p(S)*X(S)

X(t)=δ(t)

δ(t) – дельта функция

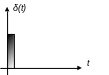
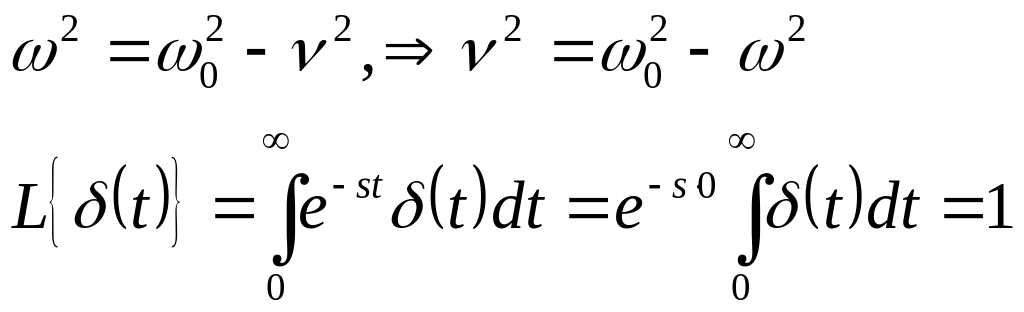
Y(S)=G_p(S)

y(t)

- импульсная переходная характеристика

Пример 1:

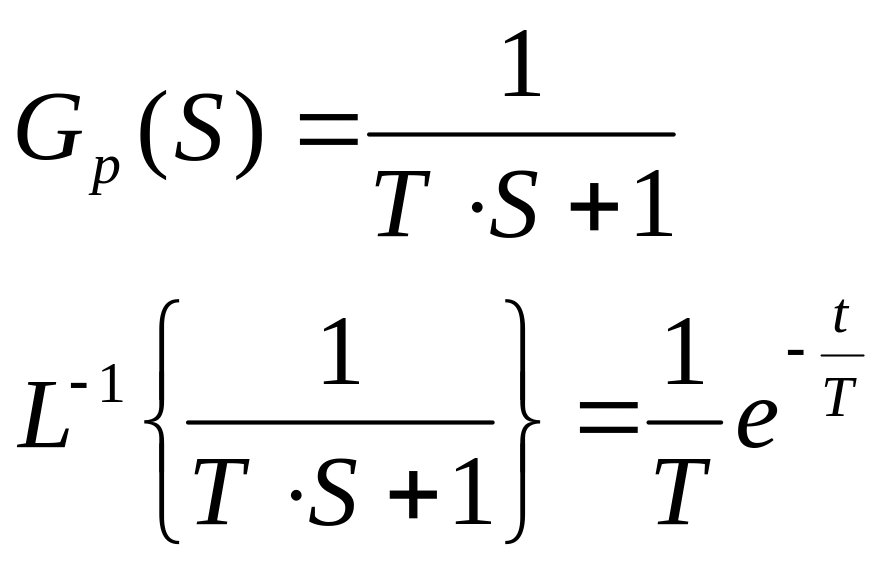
2 способа определения параметров:

а)

б) по производной:

Пример 2:

Система 2-го порядка:

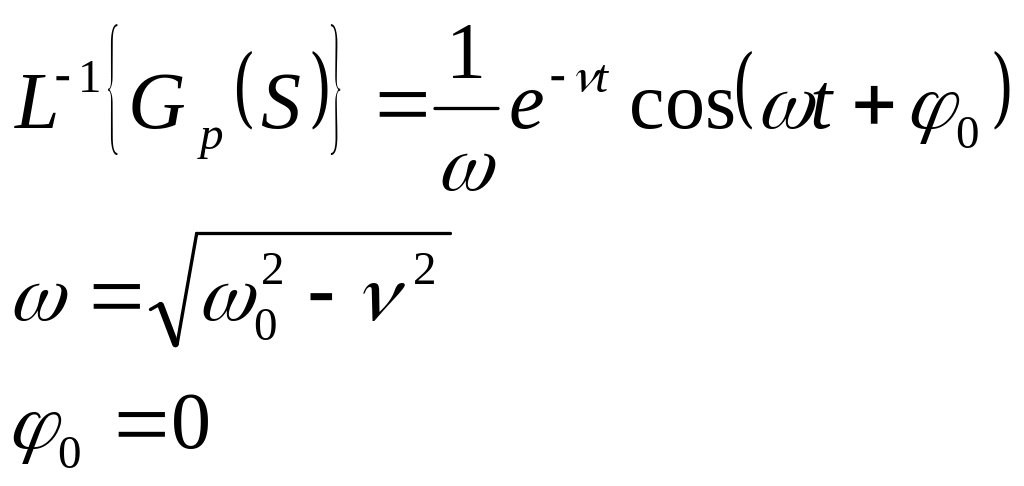
Унификация происходит по первому максимуму:

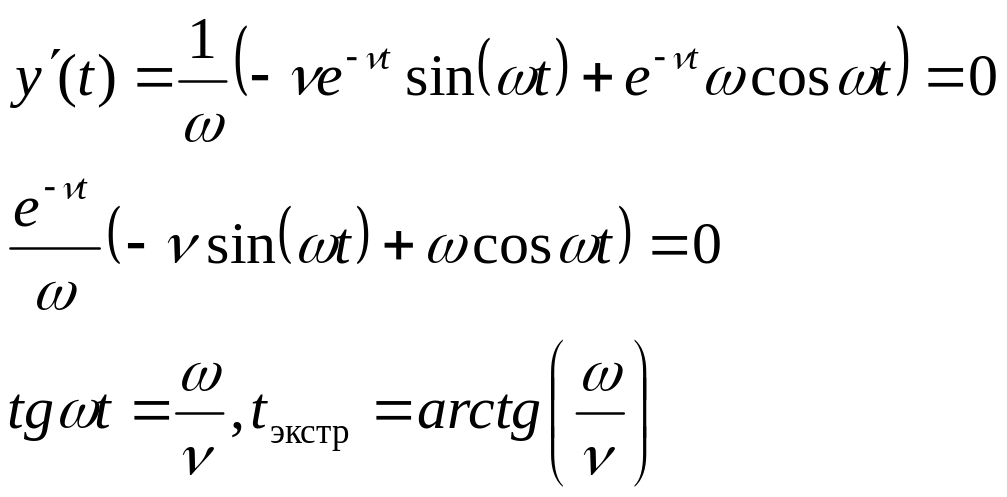
- первое условие

2 условие – измеряется частота:

два нелинейных уравнения: =>ω₀,ν

55. Идентификация динамических моделей с помощью анализа амплитудной и фазовой характеристик.

Под амплитудной характеристикой понимается зависимость .

Фазовая характеристика - зависимость отставания по фазе выходного сигнала от входного.

Пример: Колебательная система с 2 степенями свободы

Делается формальная замена: S=iw – преобразование Фурье:

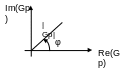
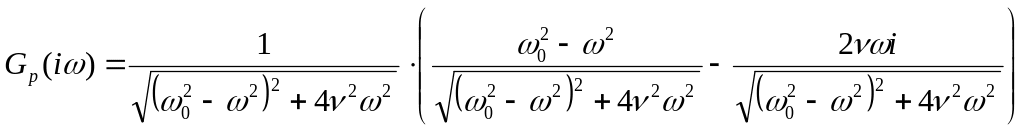
- по формуле Эйлера

Окончательно: 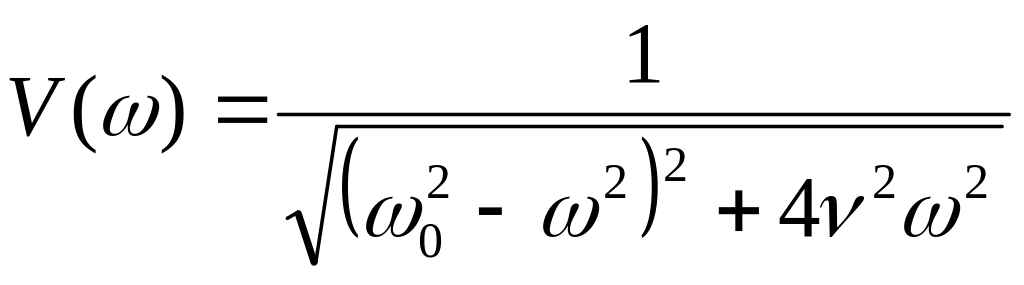- амплитудная характеристика

- фазовая характеристика

Фиксируя частоту ω, мы можем снять амплитудную характеристику, измеряя измпенение амплитуды и фазовую характеристику.

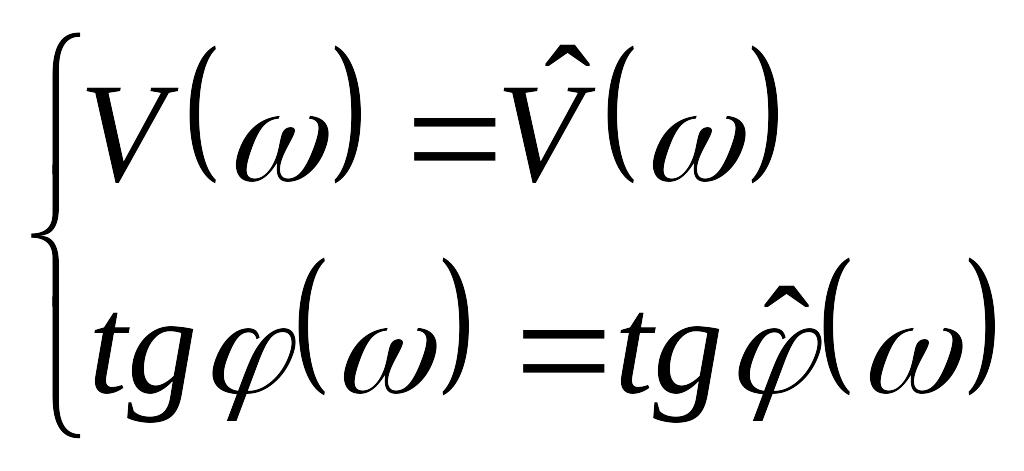(слева расчетное значение, справа - измеренное)

Откуда можно найти

56. Идентификация динамических моделей с помощью метода корреляционных функций.

Опр.:

- взаимная корреляционная функция

- частное решение для линейной системы

x(0)=0

Рассмотрим частный случай: y,x – скалярные величины

Скалярная система:

Получаем следующее:

Замена переменных:

Получаем интеграл:

Коррел. ф-ции связаны также, как и входные и выходные сигналы в линейной системе:

Если на вход подается белый шум, то коррел. ф-ция

- импульсная переходная характеристик

Вывод: подавая белый шум на линейную систему, мы вычисляем коррел. ф-цию и тем самым снимаем импульсную переходную характеристику данной системы, а по ней проводим идентификацию линейной системы.