37. Решение разностных уравнений.

- разностное уравнение

n – порядок разностного уравнения

Система разностных уравнений:

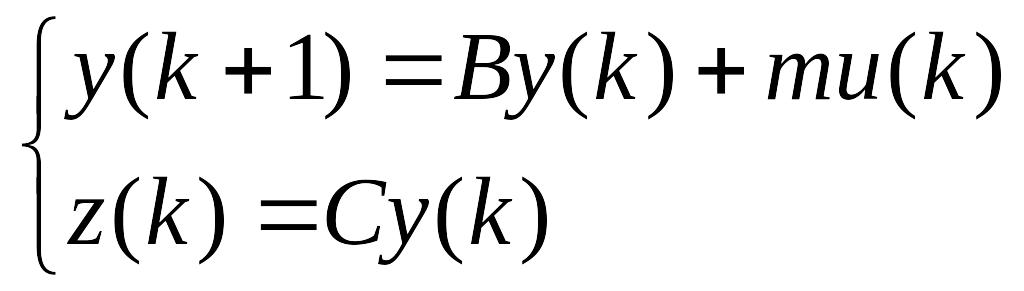
Способы решения разностных уравнений:

1) Итерационный способ

2) С помощью Z-преобразований

Итерационный способ

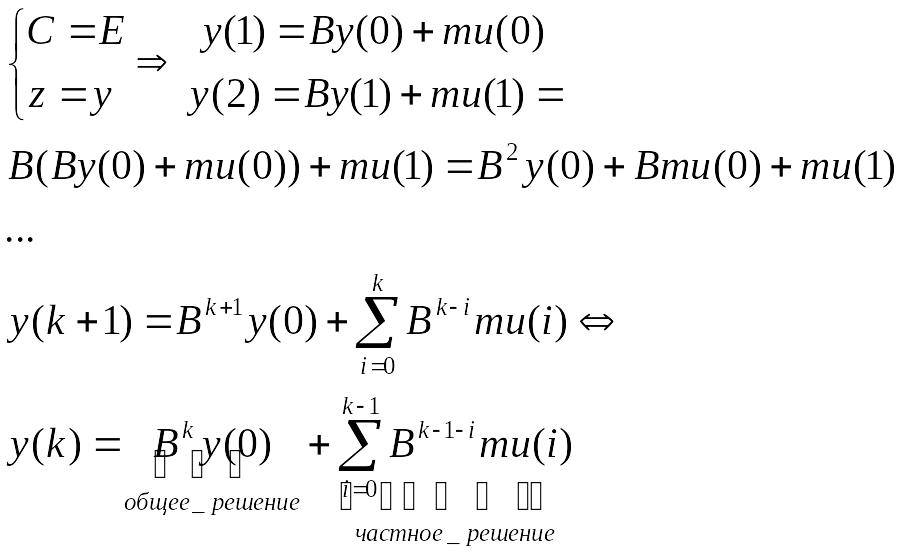
С помощью Z-преобразований

Пример

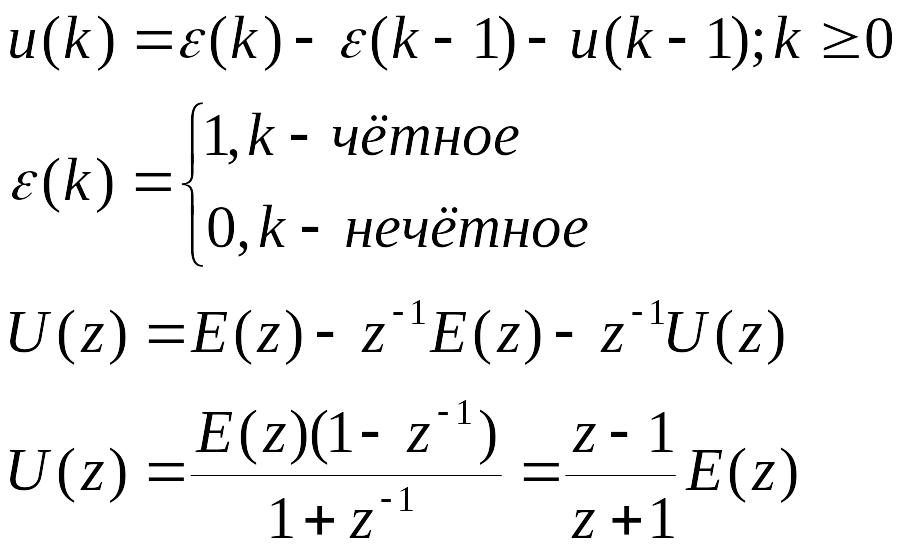
Зададим Z-преобразование для исходной последовательности:

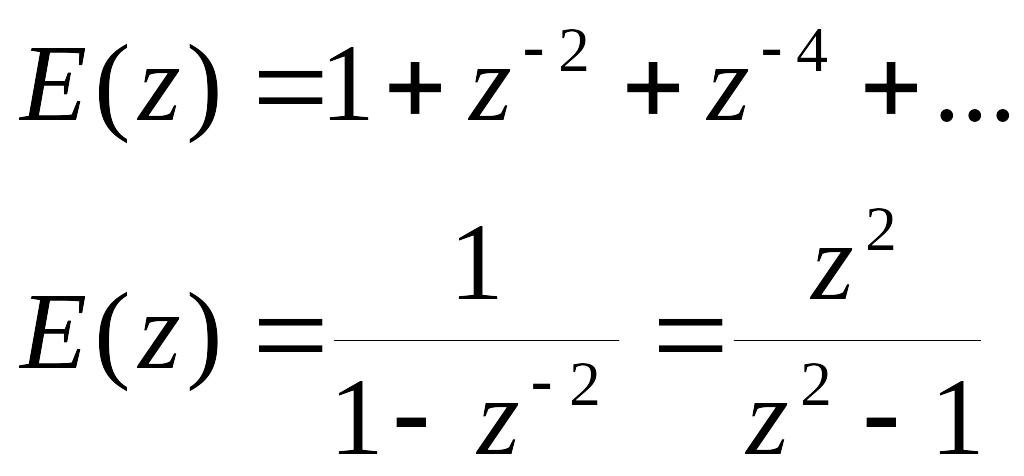
Выразим выходной сигнал:

После деления многочлена z² на z²+2z+1 получим:

=>

38. Обратное z – преобразование.

1)

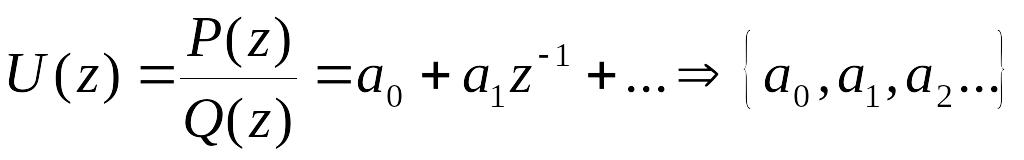
2) Использование таблиц Z-преобразований

р азлагается на простые дроби, для которых в таблице есть

Z-преобразование

{1}
{k}
{ak}
{kak}
{sin(ak)}

Пример

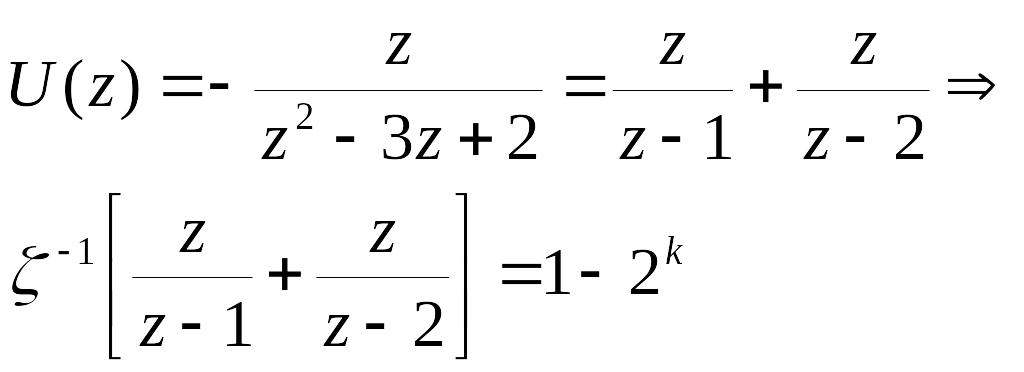
, где k=0,1,2…

39. Модели дискретных систем в пространстве состояний. Схемы моделирования.

40. Импульсные системы управления. Квантователь и экстраполятор нулевого порядка.

41. Преобразование со звездочкой и его свойства.

42. Передаточные функции разомкнутых импульсных систем.

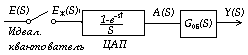,где G_об – передаточная ф–ция объекта управления

– передаточная функция в классической теории автоматического управления

; _;

;

Утверждение: ; ; ;

Доказательство:

Согласно определению ; - частота квантования;

i – мнимая единица

Периодическая функция с периодом

Б)

; ;

В)

Разомкнутые системы, содержащие цифровые регуляторы

Схема моделирования:

D(Z); ; ЦР – решение разностных уравнений

43. Передаточные функции замкнутых импульсных систем.

Замкнутые импульсные системы. Основополагающим является принцип обратной связи.

Составим передаточную функцию замкнутой системы.

Выразим ошибку

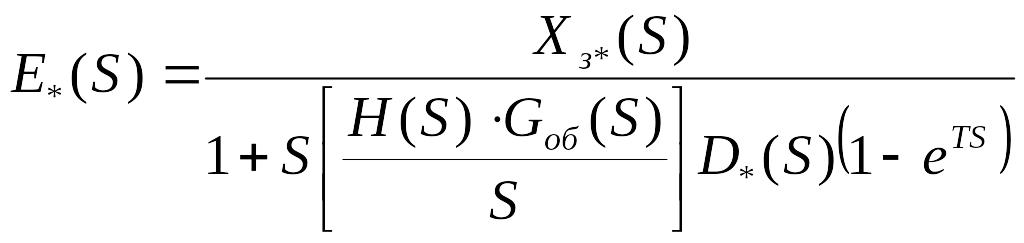
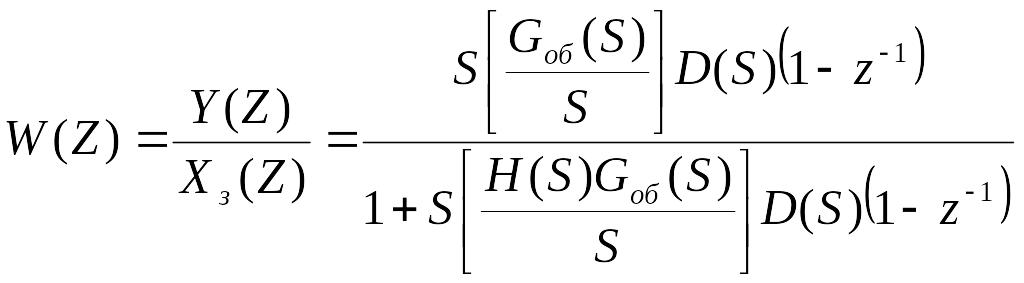
- передаточная функция общей замкнутой системы

44. Переход от непрерывных к дискретным динамическим системам в пространстве состояний.

45. Устойчивость линейных дискретных систем. Связь S- плоскости с Z- плоскостью.

46. Критерий устойчивости Джури.

47. Метод корневого годографа для непрерывных и дискретных систем управления.

Н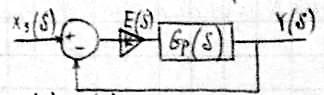 епрерывные системы управления.

k - коэффициент усиления

Пусть , тогда => ,

Необходимо выбрать k исходя из качества системы:

1. устойчивость

2. вид переходного процесса

3. установившиеся ошибки

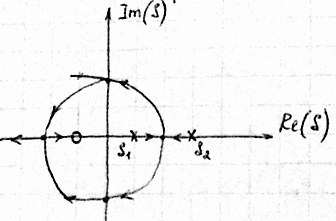
Опр: под корневым годографом понимается траектория корней характеристического уравнения на комплексной плоскости для данной системы уравнений.

Свойства корневого годографа:

1) Количество ветвей корневого годографа совпадает с порядком n системы уравнений.

2) Траектории корней на плоскости S симметричны относительно оси абсцисс.

3) Если k=0 P(S)=0 => определяются полюса передаточной функции разомкнутой системы

если

Переписывают характеристическое уравнение:

=> получаем нули перед ф-и разомкнутой системы

Траектории корней начинаются в полюсах разомкнутой системы и заканчиваются в нулях разомкнутой системы при

4) Если - количество полюсов , а - количество нулей и > , то

ветвей корневого годографа уходят в бесконечность.

Пример:

Характер. Полином для замкнутой системы:

=>

=>

Решим квадратное уравнение:

Если , то происходит отрыв от оси абсцисс:

Если ,

Если , то имеем колебательный переходный процесс.

Если или , то апериодический переходный процесс.

Условие устойчивости:

- система устойчива

Каждый корень порождает частные решения: и

Их линейная комбинация дает целое решение: Если , то

Рассмотрим дискретную систему:

Э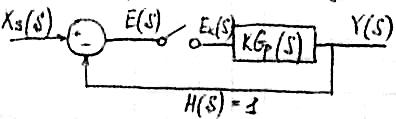 кстраполятор 0-ого порядка преобразует дискретный сигнал в непрерывный.

, - передаточная функция объекта

Все свойства корневого годографа для дискретной системы полностью сохраняются. Однако вид КГ другой. Область устойчивости – единичный круг.

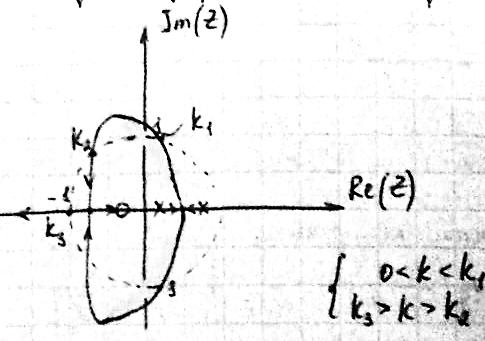– Система устойчива.