Интерполяционный многочлен Лагранжа

Коэффициенты многочлена (6.1) можно найти из того условия, что аппроксимирующая кривая должна проходить через все n+1 заданные точки. Задача в этом случае сводится к решению системы линейных уравнений

- - - - - - - - - - - - - (6.2)

,

где неизвестными являются коэффициенты a₀, a₁,...a_n.

В форме записи степенного многочлена, предложенной Лагранжем,

y=y₀.Q₀(x)+y₁.Q₁(x)+...+y_n.Q_n(x) (6.3)

коэффициенты отсутствуют и поэтому отпадает необходимость решения системы уравнений (6.2).Значения функций Q_i(x) в узловых точках дол-жны удовлетворять двум условиям:

1.В i-той узловой точке при x=x_i Q_i(x_i)=1.

2.Во всех узловых точках кроме i-той при ki Q_i(x_k)=0.

То же самое, но более компактно

(6.4)

Эти условия выполняются следующей функцией:

. (6.5)

Объединяя (6.3) и (6.5) получают:

(6.6)

или

, где . (6.7)

Блок-схема функции расчета многочлена Лагранжа представлена на рис. 6.1.

Текст функции расчета многочлена Лагранжа

function lagr(n:integer;xp:real;x,y:vec):real;

var i,k:integer;yp,q:real;

begin yp:=0;

for i:=0 to n do

begin q:=1;

for k:=0 to n do

if k<>i then

q:=q*(xp-x[k])/(x[i]-x[k]);

yp:=yp+q*y[i]

end;

lagr:=yp

end;

yp=0

i=0, n

Q=1

k=0, n

нет

ki

да

Q=Q(xp-x_k)/(x_i-x_k)

yp=yp+y_kQ

конец функции

Рис. 6.1. Блок-схема функции

расчета многочлена Лагранжа

Недостатком интерполяции степенными полиномами является возможность больших отклонений значений интерполирующего полино-ма от истинных значений функции вне узловых точек. Поскольку погрешность возрастает с увеличением количества узловых точек следу-ет стремиться к ограничению их числа.

Пример

Для заданной функции в диапазоне от 2.0 до 5.0 со-ставить таблицу значений функции в 4-х равноотстоящих узловых точ-ках. С помощью интерполяционного многочлена Лагранжа рассчитать приближенное значение функции в середине диапазона. Приближенное значение сравнить с точным и определить погрешность в процентах.

Текст программы

program interpol;

uses crt;

const n=3;

type vec=array[0..n] of real;

var h,xp,yp,xn,xk,yt,d:real;

i:integer; x,y:vec;

{- - - - - - - - - - - -}

function f(t:real):real;

var a,b,z:real;

begin a:=0.7; b:=0.65;

z:=4*sqr(sin(t+1.7));

f:=z/b/exp(1/3*ln(4*t/a))/ln(t)

end;

{- - - - - - - - - - - -}

function lagr(n:integer;xp:real;x,y:vec):real;

var i,k:integer;yp,q:real;

begin yp:=0;

for i:=0 to n do

begin q:=1;

for k:=0 to n do

if k<>i then

q:=q*(xp-x[k])/(x[i]-x[k]);

yp:=yp+q*y[i]

end; lagr:=yp

end;

{- - - - - - - - - - - -}

begin window(1,1,80,25);textbackground(0);clrscr;

xn:=2.0; xk:=5.0; h:=(xk-xn)/n;

window(25,1,55,15);textbackground(4);

textcolor(15);clrscr;

writeln(' Таблица исходных данных');

writeln(' i x y');

for i:=0 to n do

begin x[i]:=xn+i*h; y[i]:=f(x[i]);

writeln(' ':5,i,x[i]:10:2,y[i]:10:3)

end; xp:=(xn+xk)/2; yp:=lagr(n,xp,x,y);

yt:=f(xp); d:=abs((yp-yt)/yt)*100;

window(20,16,60,20);textbackground(1); clrscr;

writeln(' Вывод результатов');

writeln(' xp=',xp:4:2,' yt=',yt:6:3,

' yp=',yp:6:3,' d=',d:6:2)

end.

Результаты

Таблица исходных данных

i x y

0 2.00 1.106

1 3.00 2.172

2 4.00 0.474

3 5.00 0.205

Вывод результатов

xp=3.50 yt=1.412 yp=1.407 d=0.41

Рабочее задание

Для функции, указанной в списке вариантов, в заданном диапазоне составить таблицу значений в 4-х равноотстоящих точках. С помощью итерационного многочлена Лагранжа рассчитать приближенные значения функции в серединах всех трех участков. Приближенные значения сравнить с точными и определить погрешности в процентах.

Написать отчет, содержащий:

-задание;

-принятые обозначения;

-программу;

-результаты.

Варианты заданий к лабораторной работе 6

Таблица 6.1.

№ вари анта	Аргумент	Константы	Функция
1	2	3	4
1	xn=1.7 xk=5.3	a=0.5
2	xn=0.2 xk=1.7	b=2.1	y=
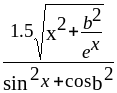
3	xn=0.7 xk=2.5	a=1.2 b=2.0 c=0.5
4	xn=1.2 xk=3.0
5	xn=1.2 xk=3.0	b=1.75
6	xn=1.2 xk=2.4	a=0.2

Продолжение табл. 6.1

1	2	3	4
7	xn=1.2 xk=2.2	a=0.5
8	xn=1.2 xk=3.0	a=0.33
9	xn=1.1 xk=2.9	0.91
10	xn=0.7 xk=1.9	a=2.73
11	xn=0.2 xk=1.7	a=3.5
12	xn=0.1 xk=0.9	a=1.3

Продолжение табл. 6.1

1	2	3	4
7	xn=1.2 xk=2.2	a=0.5
8	xn=1.2 xk=3.0	a=0.33
9	xn=1.1 xk=2.9	0.91
10	xn=0.7 xk=1.9	a=2.73
11	xn=0.2 xk=1.7	a=3.5
12	xn=0.1 xk=0.9	a=1.3

Продолжение табл. 6.1

1	2	3	4
13	xn=0.3 xk=1.5
14	xn=0.1 xk=0.6	a=0.2
15	xn=0.5 xk=2.0
16	xn=1.0 xk=2.0	a=2.1
17	xn=1.0 xk=3.0	a=0.5 b=2.1
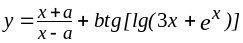
18	xn=2.0 xk=5.0	a=0.7 b=0.65

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Ивашкин Ю.А.Вычислительная техника в инженерных расчетах (мяс-ная и молочная промышленность).-М.:Агропромиздат,1989.-335 с.

2. Вычислительная техника в инженерных и экономических расчетах/ под ред. А.И.Петрова/.-М.:Высш. шк.,1984.-320 с.

3. Турчак Л.И. Основы численных методов.-М.:Наука,1987.-320 с.

4. Фаронов В.В. Программирование на персональных ЭВМ в среде Турбо Паскаль.-М.:Изд-во МГТУ,1992.-448 с.

5. Бородин А.В., Ивашкин Ю.А., Лысиков В.Т., Токарева М.А. Решение алгебраических уравнений и вычисление функций. Методические указания к выполнению лабораторных работ.-М.:МИПБ,1991.-46 с.

СОДЕРЖАНИЕ

Введение 3

Лабораторная работа 1. Вычисление функций 3

Лабораторная работа 2. Решение уравнений с одной неизвестной 6

Лабораторная работа 3. Решение систем линейных уравнений пря-

мыми методами 14

Лабораторная работа 4. Итерационные методы решения систем

линейных уравнений 22

Лабораторная работа 5. Численное интегрирование 27

Лабораторная работа 6. Интерполирование функций 37

Библиографический список 45

45