28. Преобразование координат: а) параллельный перенос б) поворот.

Параллельный перенос. Передвинем систему координат XОY в плоскости так, чтобы оси OX и OY оставались параллельны самим себе, а начало координат О сместилось в точку О' ( a, b ). Получим новую систему координат X'O'Y' 

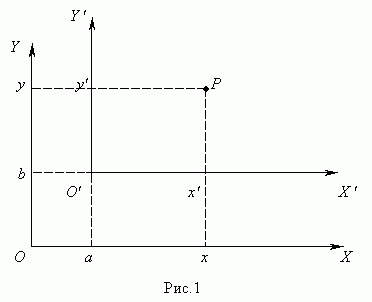
Координаты точки  Р  в новой и старой системе координат связаны соотношениями:

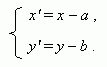
Поворот вокруг начала координат. Повернём систему координат XОY в плоскости на угол   ( рис.2 ).

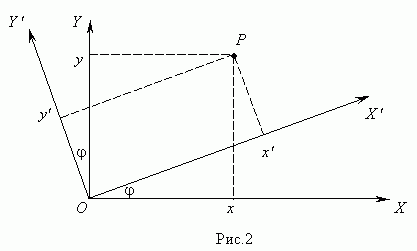
Теперь координаты точки  Р  в новой и старой системе координат связаны соотношениями:

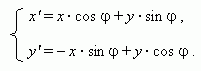
В частном случае    =    получим центральную симметрию относительно начала координат О :

 

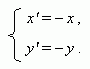
29. Анализ уравнения кривой 2-го порядка: приведение к каноническому виду.

В уравнении имеются квадраты обеих неизвестных. Преобразуем левую часть заданного уравнения, выделяя полные квадраты:

Следовательно, уравнение можно записать в виде  . Делая замену 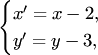  или, выражая старые координаты через новые: 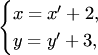 , получаем   — каноническое уравнение пары пересекающихся прямых

30. Дифференциал дуги плоской кривой. Понятие кривизны плоской линии и её вычисление при различных способах задания линии (вывод).

Если элементарная кривая L есть образ отрезка [а, в], при взаимно однозначном и непрерывном отображением F:[a, в]→ R³ , то положение любой точки М на кривой L определяется параметром t [a, в].

Таким образом, координаты точки М являются некоторыми функциями от t

Функции f₁, f₂, f₃ описывают параметризацию F кривой L и называется координатными функциями.

Если f:[а, в]→R² непрерывная функция, то графиком является плоская кривая, допускающая параметризацию

Если можно выразить х, то такая функция называется явное задание функции. Не все кривые допускают явное задание.

Пусть F параметризация кривой L а f₁, f₂, f₃ её координатные функции. Параметризацией называется регулярной если функции f₁, f₂, f₃ гладкие (неоднократно дифференцируемые) и при каждом значение параметра t значение производной покрайне мере одно из координатных функций отлично от нуля. (f₁^| )²+ (f₂^|)² + (f₃^| )² ≠0

Каждая параметризация определяет некоторый порядок точек на кривой. Что бы зафиксировать порядок точек, достаточно указать (зафиксировать) начальную и конечную точку. Кривую с фиксированным начальными и конечными точками называют оринтированые

Пусть каждому числу t принадлежащему отрезку [а, в] по некоторому правилу поставлен в соответствие (t) трехмерного жвклидового пространства, тогда говорят, что на отрезке [а, в] определена вектор функция (t).

Если отложить все векторы (t) из начала координат, то их концы образуют множество точек называемые «ГОДОГРАФОМ».

Наиболее общий способ задать уравнение пространственной кривой — параметрический:

где   — гладкие функции параметра t, причем   (условие регулярности).

Часто удобно использовать инвариантную и компактную запись уравнения кривой с помощью вектор-функции:

,

где в левой части стоит радиус-вектор точек кривой, а правая определяет его зависимость от некоторого параметра t. Раскрыв эту запись в координатах, мы получаем формулу (1).

В зависимости от свойств дифференцируемости функций  , задающих кривую, говорят о степени гладкости (регулярности) кривой. Кривая называется регулярной, если для любой её точки, при подходящем выборе прямоугольной декартовой системы координат  , она допускает в окрестности этой точки задание уравнениями вида:

,

где   и   — дифференцируемые функции.

Для того чтобы точка кривой, заданной общим уравнением (1), была обыкновенной (не особой точкой), достаточно, чтобы в этой точке выполнялось вышеуказанное неравенство

Дифференциальная геометрия рассматривает также кусочно-гладкие кривые, которые состоят из гладких участков, разделённых особыми точками. В особых точках определяющие функции либо не удовлетворяют условиям регулярности, либо вообще не дифференцируемы.