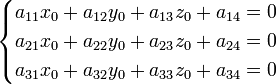25. Гипербола: вывод уравнения, исследование формы, характеристики.

Гиперболой называется множество точек плоскости (см. рис.8) , модуль разности расстояний которых до двух данных точек и (фокусов гиперболы) постоянен и равен . Фокусное расстояние обозначают через . Прямая, на которой лежат фокусы, называется действительной (или фокальной осью) гиперболы. Прямая, проходящая через центр гиперболы , перпендикулярно к действительной оси, называется мнимой осью.

Директрисой гиперболы, соответствующей данному фокусу , называется прямая , перпендикулярная к действительной оси, отстоящая от центра на расстояние и лежащая от центра по одну сторону с фокусом, где – эксцентриситет.

Гипербола имеет две асимптоты, заданные уравнениями .

Каноническое уравнение гиперболы в декартовой системе координат: ,

где и – половины сторон основного прямоугольника гиперболы.

26. Парабола: вывод уравнения, исследование формы, характеристики.

Параболой называется множество точек плоскости (см. рис.7а), для каждой из которых расстояние до данной точки (фокуса параболы) равно расстоянию до некоторой данной прямой (директрисы). Расстояние от фокуса параболы до директрисы называется параметром параболы. Парабола – симметричная кривая; точка пересечения параболы с ее осью симметрии называется вершиной параболы.

Каноническое уравнение параболы в декартовой системе координат: .

27. Поверхности второго порядка: цилиндрические, конические, поверхности вращения. Их уравнения, примеры.

Цилиндрические поверхности

Поверхность S называется цилиндрической поверхностью с образующей  , если для любой точки M₀ этой поверхности прямая, проходящая через эту точку параллельно образующей  , целиком принадлежит поверхности S.

Теорема (об уравнении цилиндрической поверхности). Если в некоторой декартовой прямоугольной системе координат поверхность S имеет уравнение f(x,y) = 0, то S — цилиндрическая поверхность с образующей, параллельной оси OZ.

Кривая, задаваемая уравнением f(x,y) = 0 в плоскости z = 0, называется направляющей цилиндрической поверхности.

Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.

Эллиптический цилиндр:	Параболический цилиндр:	Гиперболический цилиндр:
Пара совпавших прямых:	Пара совпавших плоскостей:	Пара пересекающихся плоскостей:

Конические поверхности

Поверхность S называется конической поверхностью с вершиной в точке O, если для любой точки M₀ этой поверхности прямая, проходящая черезM₀ и O, целиком принадлежит этой поверхности.

Функция F(x,y,z) называется однородной порядка m, если   выполняется следующее: 

Теорема (об уравнении конической поверхности). Если в некоторой декартовой прямоугольной системе координат поверхность S задана уравнением F(x,y,z) = 0, где F(x,y,z) — однородная функция, то S — коническая поверхность с вершиной в начале координат.

Если поверхность S задана функцией F(x,y,z), являющейся однородным алгебраическим многочленом второго порядка, то S называется конической поверхностью второго порядка. Каноническое уравнение конуса второго порядка имеет вид:

Поверхности вращения

Поверхность S называется поверхностью вращения вокруг оси OZ, если для любой точки M₀(x₀,y₀,z₀) этой поверхности окружность, проходящая через эту точку в плоскости z = z₀ с центром в (0,0,z₀) и радиусом  , целиком принадлежит этой поверхности.

В случае, если  , перечисленные выше поверхности являются поверхностями вращения.

Гиперболический параболоид

Ввиду геометрической схожести гиперболический параболоид часто называют «седлом».

Уравнение гиперболического параболоида:

При сечении гиперболического параболоида плоскостью z = z₀ поверхность порождает гиперболу.

При сечении гиперболического параболоида плоскостью x = x₀ или y = y₀ поверхность порождает параболу.

Эллиптический параболоид

Уравнение эллиптического параболоида:

Центральные поверхности

Если центр поверхности второго порядка существует и единственен, то его координаты   можно найти решив систему уравнений: