10. Векторы (основные понятия), линейные операции над векторами и их свойства.

Геометрический вектор - направленный отрезок. Длина вектора называется модулем |AB|=|a|. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора одинаковые, когда они имеют одинаковое направление и равные модули. Противоположные, когда имеют равные модули и противоположное направление. Нуль-вектор. Единичный вектор. Линейные операции над векторами: 1) Суммы 2 векторов а и в называют вектор с, соединяющий начало вектора а с концом вектора в, отложенного от конца вектора а (правило треугольника). Замечание: это правило справедливо для суммы любого конечного числа векторов. Сумму двух векторов можно построить также по правилу параллелограмма. 2) Разностью двух векторов а и в называется вектор с = вектор а – вектор в, такой что в+с=а. Заметим, что а-в=а+(-в). 3) Произведением не нулевого вектора а на число  ≠0 называется вектор, который имеет длину |  | ° |a| и соноправлен вектору а, если  >0, противоположно направлен, если  <0. в =  ° а – условие коллинеарности векторов. с =  ₁ ° а +  ₂ ° в – условие комплонарности

( _1,  ₂ R( ₁²+  ₂²≠0)) Свойства линейных операций

1) a+b=b+a

2) (a+b)+c = a+(b+c)

3) a+0=a

4) a+(-a)=0

5)  ° (β ° а) = ( ° β) ° а

6) ( + β) ° а =  ° а + β ° а

7)  ° (а + в) =  ° а +  ° в

Проекция вектора на ось – Определение: проекцией вектора а на ось L называется число равное длине вектора А₁В₁ взятой со знаком «+», если направление векторов А₁В₁ совпадает с направлением оси L, со знаком «-» в противном случае (точки А₁В₁ есть основания перпендикуляров, опущенных из начальной и конечной точки вектора а на ось L). Если вектора i,j,k – орты координатных осей прямоугольной системы координат Оxyz, то любой вектор а единственным образом можно представить в виде линейной комбинации, ортов i,j,k с координатами a_x, a_y, a_z. (a = a_x ° i + a_y ° j + a_z ° k) Коэффициенты a_x, a_y, a_z - это координаты вектора а (проекция вектора а на оси Ox, Oy, Oz соответственно)

1) векторы а и в равны тогда и только тогда, когда равны их соответствующие координаты (a_x = в_x, a_y = в_y, a_z = в_z); 2) векторы а и в коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны (вектор а || вектору в ); 3) при умножение вектора на число  ≠0 все координаты этого вектора умножаются на заданное число ( ° а = {  ° a_x;  ° a_y;  ° a_z;}); 4) при сложение векторов их соответствующие координаты складываются

(а + в = { a_x + в_x; a_y + в_y; a_z + в_z }) (а – в = a + (-1) ° в = { a_x - в_x; a_y - в_y; a_z - в_z });

Вектор r равен вектору ОМ соединяющий начало координат с произвольной точкой М (x; y; z) называется радиус – вектором точки М. Расстояние между точками А и В находятся как длина вектора АВ:

11. Линейная зависимость и независимость векторов (определение, свойства, в координатной форме).

Определение: а₁, а₂,…, а_n называется линейно зависимыми, если их линейная комбинация = 0. ₁ ° а₁ + ₂ ° а₂ + … + _n ° a_n = 0, где коэффициенты ₁, ₂, _n не все одновременно = 0, в противном случае данные векторы называются не зависимые

Теорема: Если а₁, а₂,…, a_n – линейно зависимые, то один из них всегда можно выразить в виде линейной комбинации всех остальных векторов. Доказательство:

₁ ° а₁ + ₂ ° а₂ + … + _n-1 ° a_n-1 + _n ° a_n = 0. Линейно зависимое например, _n ≠0.

_n ° a_n = -₁ ° а₁ - ₂ ° а₂ - … - _n-1 ° a_n-1 |: _n

a_n = - ₁/_n ° а₁ – ₂/_n ° а₂ - … -_n-1/_n ° а_n-1

Пусть - _i/_n = μ_i (i=1,2,…,n-1)

a_n = μ₁ ° а₁ + μ₂ ° а₂ + … + μ_n-1 ° а_n-1

Обратная теорема: Если вектор an выражается с помощью линейной комбинации

а₁, а₂,…, a_n-1 , то а₁,а₂,…, a_n-1, a_n Линейно зависимые

12. Базис векторного пространства; теорема о разложении вектора по базису (до-казательство).

1) На координатной прямой любые два вектора линейно зависимые (т.к. они кллинеарны) По определению коллинеарности:

в =  ° а ,  ≠0

 ° а + (-1) ° в = 0 (векторы а и в линейно зависимые)

2) На плоскости любые два коллинеарны вектора линейно зависимые и наоборот а не || в (вектор а и в линейно независимые)

Любые 3 вектора на плоскости линейно зависимы

Доказательство: Возможны 2 случая: 1) среди данных векторов имеется пора коллинеарных (в=°а (т.е. а || в ) представим в=а+0°с; °а+(-1)°в+0°с=0)

2) среди векторов а, в, с нет коллинеарных, выпустим из ощего начала, покажем, что например вектор с может быть представлен в виде линейной комбинации векторов а и в. (ON = OM + OK (т.к. OM || a => OM = ₁ ° a; OK || в => ₂ ° в; ₁, ₂ R =>

с = ₁ ° а + ₂ ° в ; ₁ ° а + ₂ ° в + (-1) ° с = 0)

Следствие: Если число данных векторов на плоскости больше трех, то они так же линейно зависимы. Любые 4 вектора в пространстве линейно зависимы. Если число векторов больше 4 в пространстве, то они так же ЛЗ. Для того, чтобы 3 вектора в пространстве были комплонарны необходимо и достаточно, чтобы они были ЛЗ. Для того чтобы 3 вектора а, в, с были ЛНЗ необходимо и достаточно, чтобы они были не комплонарны. Max число ЛНЗ векторов: на координатной прямой один, на плоскости два, в трех мерном пространстве три. Базисом линейного пространства называется max возможное число ЛНЗ векторов. Основное значение базиса состоит в том, что линейные операции над векторами при задание базиса, становятся линейными операциями над числами – координат этих векторов в заданном базисе. Пусть векторы а, в, с – базис и известны разложения векторов p и q в этом базисе т.е. векторы p и q представлены в виде линейных комбинаций в базисах

p = ₁ ° a + ₂ ° в + ₃ ° c; q = M₁° a + M₂ ° в + M₃ ° c; p + q = (₁ + M₁) ° a + (₂ + M₂) ° в + (₃ + M₃) ° c; Если k-const (k ° p = (k ° ₁) ° a + (k ° ₂) ° в + (k ° ₃) ° c )

Замечание: векторы i, j, k являются ортанормированым базисом (a=a_x ° i + a_y ° j + a_z ° k)

13. Декартова система координат. Координаты точки, координаты вектора AB. Деление отрезка AB в отношении (вывод).

Декартова система координат.

Зафиксируем в пространстве точку О и рассмотрим произвольную точку М.

Вектор   назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора.

            Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.

1-я ось – ось абсцисс

2-я ось – ось ординат

3-я ось – ось апликат

            Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.

Если заданы точки А(x₁, y₁, z₁),   B(x₂, y₂, z₂), то  = (x₂ – x₁, y₂ –  y₁, z₂ – z₁).

Если точка М(х, у, z) делит отрезок АВ в соотношении /, то координаты этой точки определяются как:

            В частном случае координаты середины отрезка находятся как:

x =  (x₁ + x₂)/2;         y = (y₁ + y₂)/2;            z = (z₁ + z₂)/2.

14. Проекция вектора на ось. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы.

15. Скалярное произведение векторов и его свойства. Вывод выражения в координатной форме. Приложения. Условие ортогональности двух векто-ров.

Скалярным произведением двух векторов называется число равное произведению модулю этих векторов на cos угла между ними. Свойство скалярных прозведений:

1)ab=ba; 2) а° а = |a|² ; 3) (а + в) ° с = а ° с + в ° с ; 4) ( ° а) ° в =  ° (а ° в);

5)  ° (М ° а) = ( ° М) ° а

Скалярное произведение в координатной форме: Пусть a = a_x ° i + a_y ° j + a_z ° k

в = в_x ° i + в_y ° j + в_z ° k

а ° в = (a_x ° i + a_y ° j + a_z ° k) ° (в_x ° i + в_y ° j + в_z ° k) = (a_x ° в_x) ° i² + (a_x ° в_y) ° (i ° j ) + (a_x ° в_z) ° (i ° k) + (a_y ° в_y) ° j² + (a_z ° в_z) ° k² т.о. а ° в = a_x ° в_x + a_y ° в_y + a_z ° в_z

16. Векторное произведение векторов и его свойства. Вывод выражения в координатной форме. Приложения.

Векторным произведением вектора на вектор называется вектор (другое обозначение ), который:

а) имеет длину , где – угол между векторами и ;

б) перпендикулярен векторам и ( ) (то есть, перпендикулярен плоскости, в которой лежат векторы и );

в) направлен так, что векторы , , образуют правую тройку векторов, то есть из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки

Координаты векторного произведения вектора на вектор определяются по формуле:

Геометрический смысл векторного произведения: модуль вектора равен площади параллелограмма, построенного на векторах и .

Свойства векторного произведения:

1) ; 2) ;

3) ; 4) и коллинеарны; 5) =0

a = a_x ° i + a_y ° j + a_z ° k; в = в_x ° i + в_y ° j + в_z ° k

a в = (a_x ° i + a_y ° j + a_z ° k) ( в_x ° i + в_y ° j + в_z ° k) = (a_x ° в_x) ° (i i) + (a_x ° в_y) ° (i j) + (a_x ° в_z) ° (i k) + (a_y ° в_x) ° (i j) + (a_y ° в_y) ° (j j) + (a_y ° в_z) ° (j k) + (a_z ° в_x) ° (k i) + (a_z ° в_y) ° (k j) + (a_z ° в_z) ° (k k) = (a_y ° в_z - a_z ° в_y) ° i – (a_x ° в_z - a_z ° в_x) ° j + (a_x ° в_y – a_y ° в_x) ° k

Для запоминания векторного произведения в координатной форме удобно использовать короткую запись:

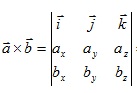
Некоторые приложения векторного произведения:

1. Условие коллинеарности векторов а || в  а в

2. Нахождение площади параллелограмма и треугольника

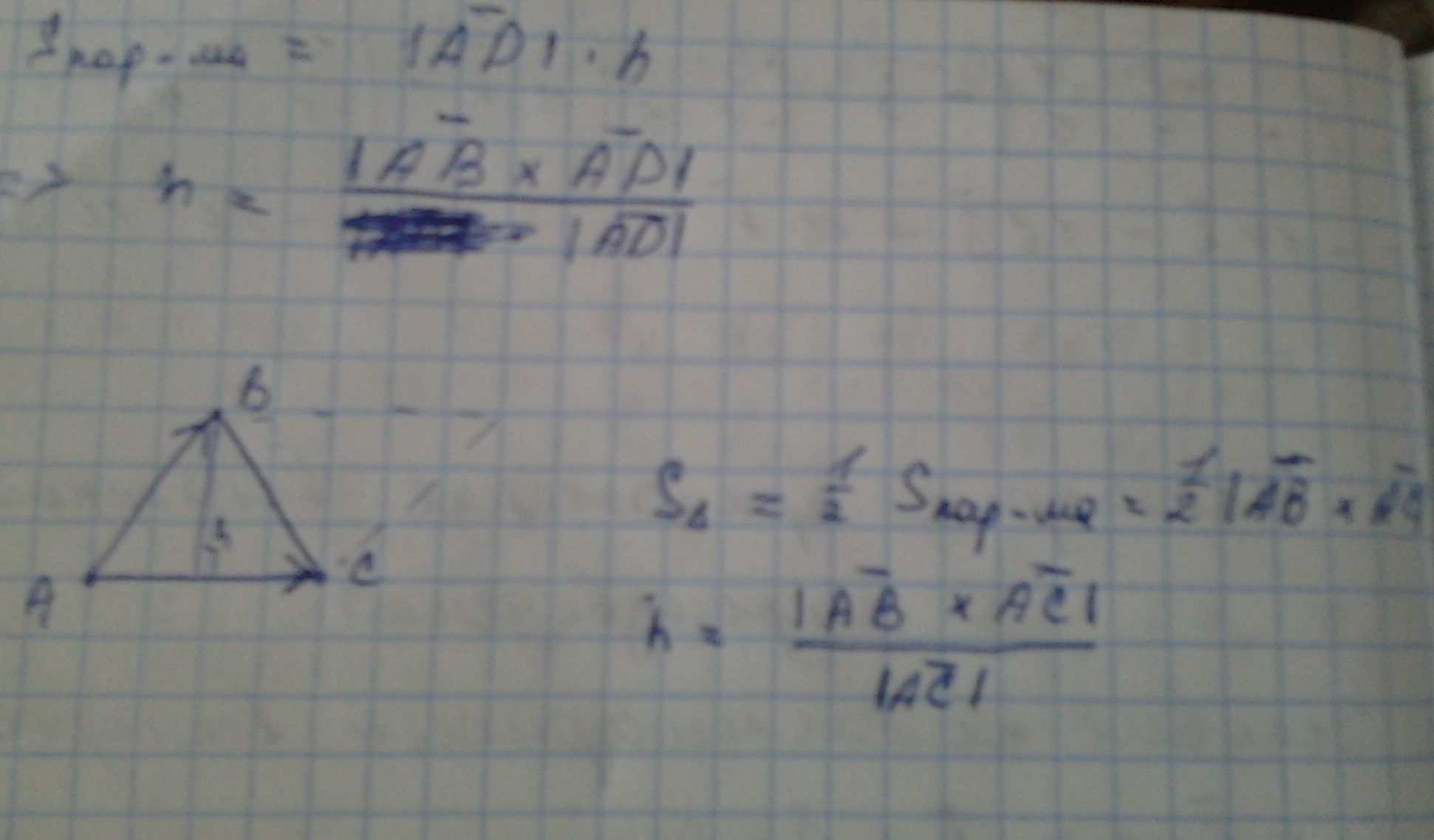
17. Смешанное произведение векторов и его свойства. Вывод выражения в координатной форме. Приложения. Условие компланарности трёх векторов.

Смешанным произведением трех векторов , , называется скалярное произведение вектора на вектор :

.

Если то смешанное произведение можно вычислить по формуле:

.

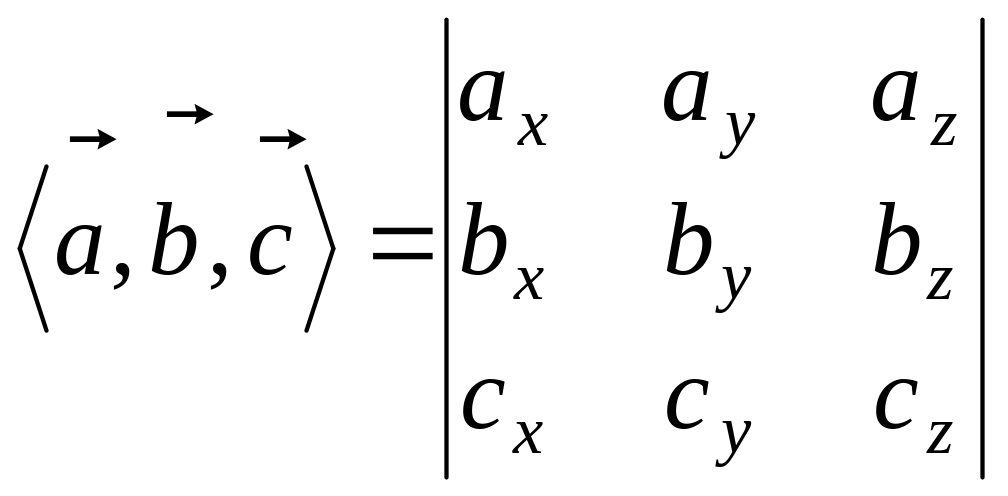Свойства смешанного произведения:

1) При перестановке любых двух векторов смешанное произведение меняет знак;

2)Смешанное произведение не меняется при циклической перестановки векторов

авс = сав = вса ; 3)Смешанное произведение не меняется при замене знаков векторного и скалярного произведения (а в) ° с = а ° (в с) ;

4)Смешанное произведение не нулевых векторов равно 0  компланарны .

Смешанное произведение в координатной форме:

a = a_x ° i + a_y ° j + a_z ° k; в = в_x ° i + в_y ° j + в_z ° k; с = с_x ° i + с_y ° j + с_z ° k

авс = (а в) ° с

Пример 4. Компланарны ли векторы , , ?

Решение. Если векторы компланарны, то по свойству 4) их смешанное произведение равно нулю. Проверим это. Найдем смешанное произведение данных векторов, вычислив определитель:

векторы , , некомпланарны.

18. Собственные векторы и собственные значения матрицы. Характеристический многочлен.

Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A, если  Av = λv, где число λ называется собственным значением матрицы A. Таким образом преобразование, которое выполняет матрица A над вектором v, сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и αv — тоже собственный вектор. 

У матрицы A , размерностью (N×N) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению  

det(A − λI) = 0, 

являющемуся алгебраическим уравнением N-го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид

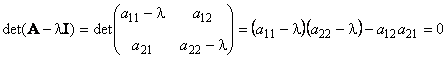
Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная (A^t = A), то ее собственные значения вещественны.