- •События и их возможные исходы
- •Функции распределения случайных величин
- •Количественные показатели надёжности
- •Восстанавливаемые элементы
- •Показатели долговечности
- •Показатели ремонтопригодности
- •Показатели сохраняемости
- •Комплексные показатели надёжности
- •Математическая модель внезапного отказа
- •Анализ закономерностей, описывающих процессы изнашивания, старения и усталостного повреждения деталей и узлов локомотивов
- •Понятие о параметрической надёжности
- •Требования к информации о надёжности, методы её сбора, анализа и автоматизации
- •Характеристика исходных предпосылок оптимизации межремонтных пробегов
- •Модель оптимизации межремонтного периода исходя из экономической целесообразности
- •Управление надёжностью локомотивного парка депо
- •Технические особенности обеспечения надёжности локомотивного парка
Функции распределения случайных величин
В любом заданном множестве данных неизбежно будет рассеяние. Да, результаты наблюдений не будут всё время одинаковыми, но это не значит, что они определяются как попало. Хотя сами значения всё время меняются, они подчиняются некоторому правилу, а в таком случае говорят, что полученные данные наблюдений или экспериментов следуют определённому распределению. Поэтому случайная величина считается заданной, если известен её закон распределения, под которым понимают – соотношение (функцию), устанавливающую связь между множеством значений случайной величины и их вероятностями.
 Прежде
всего, рассмотрим особенности функции
распределения случайной величины,
которая обозначается
Прежде
всего, рассмотрим особенности функции
распределения случайной величины,
которая обозначается
 .
Указанная функция универсальна, поскольку
может быть использована для описания
как дискретных, так и непрерывных
случайных величин.
.
Указанная функция универсальна, поскольку
может быть использована для описания
как дискретных, так и непрерывных
случайных величин.

Рис. 2.1. График функции распределения вероятностей дискретной случайной величины
Функция
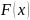 выражает вероятность того, что значения
переменной Х
не превосходят заданного значения х.
Она определена для всех значений х
между
выражает вероятность того, что значения
переменной Х
не превосходят заданного значения х.
Она определена для всех значений х
между
 и принимает значения от нуля до единицы
включительно:
и принимает значения от нуля до единицы
включительно:

При
этом
 Поэтому функция
Поэтому функция
 монотонно не убывающая: при
монотонно не убывающая: при

Вероятность попадания случайной величины в полуинтервал [ x1, x2 ) определяется по формуле

На рис.2.1 показан типичный ступенчатый вид графика функции распределения дискретной случайной величины. Поскольку непрерывная случайная величина дифференцируема, то вид её функции распределения уже не ступенчатый, а непрерывный, как показано на рис 2.2.
Р ис.
2.2. График функции распределения
вероятностей непрерывной случайной
величины
ис.
2.2. График функции распределения
вероятностей непрерывной случайной
величины
График
функции распределения дискретной
случайной величины напоминает лестницу.
Вертикальные отрезки графика в точности
соответствуют значениям анализируемой
случайной величины
 .
В промежутках между анализируемыми
значениями других чисел нет, поэтому
вероятность не изменяется, что и
представляется горизонтальными участками
графика. Высота скачков в каждой из
восьми натуральных точек равна
вероятности, с которой переменная
принимает соответствующее значение.
.
В промежутках между анализируемыми
значениями других чисел нет, поэтому
вероятность не изменяется, что и
представляется горизонтальными участками
графика. Высота скачков в каждой из
восьми натуральных точек равна
вероятности, с которой переменная
принимает соответствующее значение.
Таким
образом, функция
![]() является мерой вероятности, накопленной
на всём интервале от
является мерой вероятности, накопленной
на всём интервале от
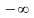 до x
включительно, т.е. кумулятивной
вероятности. При
до x
включительно, т.е. кумулятивной
вероятности. При

Вероятность
попадания случайной величины в
полуинтервал
![]() определяется по формуле
определяется по формуле
![]()
Но
накопление вероятностей в случае
дискретной и непрерывной случайных
величин происходит по-разному. В первом
случае (см. рис.2.1) горизонтальные отрезки
графика соединяются вертикальными
отрезками или скачками вероятности. Во
втором случае (см. рис.2.2) график растёт
плавно, что свидетельствует о непрерывном
возрастании функции распределения.
Если мы знаем характер изменения функции
распределения вероятностей
,
то, задав величину вероятности
 ,
можно достаточно просто, используя
график
,
можно достаточно просто, используя
график
 ,
найти значение случайной величины
,
найти значение случайной величины
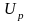 ,
как показано на рис. 2.2. Полученное
значение называют квантилью. Квантиль
– это значение случайной величины,
соответствующее заданной вероятности.
,
как показано на рис. 2.2. Полученное
значение называют квантилью. Квантиль
– это значение случайной величины,
соответствующее заданной вероятности.
Отмеченное различие отражает неодинаковую природу исходных переменных величин: в первом случае переменная дискретна, а во втором – непрерывна, поскольку принимает все значения от нуля до единицы, как бы пробегая их непрерывно, в то время как в первом случае значениями являются вполне определённые дискретные точки, например, х1, х2 … х8.
Функция распределения даёт нам один из возможных способов представления вероятностных оценок значений некоторой переменной (случайной) величины. Эта функция удобна тем, что ею можно пользоваться как в случае дискретных, так и непрерывных случайных величин. Причём, всякую непрерывную случайную величину можно задать в виде дискретной, если все возможные её значения разбить на интервалы и задать вероятности появления этих интервалов (из-за ограниченности измерительных средств все замеры непрерывных величин задаются в дискретном виде).
Существует,
однако, и иное представление вероятностных
оценок, интуитивно более оправданное
и геометрически лучше интерпретируемое.
Так, например, отличительным свойством
функции распределения дискретной
случайной величины является наличие
последовательности горизонтальных
линий на её графике, соединённых между
собой вертикальными отрезками (скачками,
ступенями), как показано на рис.2.1. Чтобы
описать скачок формально, предположим,
что он происходит в точке
 .
В основании ступени значение функции
распределения составляет
.
В основании ступени значение функции
распределения составляет
 ,
а на вершине ступени оно равно
,
а на вершине ступени оно равно
 .
Разность между этими значениями и есть
.
Разность между этими значениями и есть
 .
Эту функцию обозначили
.
Эту функцию обозначили
 и
назвали функцией вероятностей переменной
(случайной) величины
.
и
назвали функцией вероятностей переменной
(случайной) величины
.
Поэтому
дискретную случайную величину можно
задать с помощью таблицы, в одной строке
которой перечислены возможные значения
этой величины
![]() ,
а в другой – вероятности
,
а в другой – вероятности
![]() событий, состоящих в том, что случайная
величина
примет конкретное значение
:
событий, состоящих в том, что случайная
величина
примет конкретное значение
:
 .
.
|
|
|
|
… |
|
… |
|
|
|
|
|
… |
|
… |
|
При
этом сумма всех вероятностей появления
значений случайной дискретной величины
 ,
т.е. случайная величина в процессе
проведения эксперимента обязательно
примет одно из перечисленных в таблице
значений
.
,
т.е. случайная величина в процессе
проведения эксперимента обязательно
примет одно из перечисленных в таблице
значений
.
Во
втором случае переменная
является непрерывной случайной величиной.
Когда
пробегает значения от
 до
до
 ,
вероятности накапливаются непрерывно.
Таких крупных «вкладов» в общую сумму,
как могла внести одна точка в случае
дискретной переменной, здесь не будет.
Поэтому в случае анализа непрерывной
случайной величины нельзя, указав точку
,
спросить, какова вероятность того, что
именно она окажется интересующим нас
частным значением. Более оправданным
будет вопрос о скорости аккумуляции
вероятностей для каждого значения
.
Скорость, с которой аккумулируется или
накапливается вероятность, задаёт
тангенс угла наклона графика функции
распределения вероятностей
к оси абсцисс. Чем круче наклон графика,
тем быстрее идёт накопление вероятностей
в функции распределения
.
,
вероятности накапливаются непрерывно.
Таких крупных «вкладов» в общую сумму,
как могла внести одна точка в случае
дискретной переменной, здесь не будет.
Поэтому в случае анализа непрерывной
случайной величины нельзя, указав точку
,
спросить, какова вероятность того, что
именно она окажется интересующим нас
частным значением. Более оправданным
будет вопрос о скорости аккумуляции
вероятностей для каждого значения
.
Скорость, с которой аккумулируется или
накапливается вероятность, задаёт
тангенс угла наклона графика функции
распределения вероятностей
к оси абсцисс. Чем круче наклон графика,
тем быстрее идёт накопление вероятностей
в функции распределения
.
Теперь
можно определить новую функцию, которую,
как и в предыдущем случае, будем обозначать
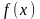

Или в более наглядном виде

Рис. 2.3. Функция плотности распределения вероятностей или кривая распределения
Числитель
выражения в квадратных скобках – есть
вероятность того, что
находится в интервале
 ,
а знаменатель – длина этого интервала.
Таким образом,
это мера плотности вероятностей в точке
.
,
а знаменатель – длина этого интервала.
Таким образом,
это мера плотности вероятностей в точке
.
При
анализе непрерывных случайных величин
функцию
называют
функцией плотности вероятностей
переменной (случайной)
или просто функцией плотности вероятностей.
Чтобы получить функцию плотности
вероятностей непрерывной случайной
величины
из
функции распределения вероятностей
 ,
нужно последнюю просто продифференцировать.
График функции
часто называют кривой распределения
(см. рис.2.3).
,
нужно последнюю просто продифференцировать.
График функции
часто называют кривой распределения
(см. рис.2.3).
Поскольку
действия дифференцирования и интегрирования
взаимосвязаны, а
является
производной от
,
то функция
,
в свою очередь, должна получаться из
![]() путём интегрирования
путём интегрирования
 .
.
Геометрически
такая запись попросту означает, что
─ площадь под той частью кривой
распределения
,
которая расположена левее
![]() .
Вероятность попадания случайной величины
в промежуток
.
Вероятность попадания случайной величины
в промежуток
 равна
равна
 .
.
Это площадь криволинейной трапеции на рис. 2.3, которая образуется под частью кривой , заключённой между точками и . Итак, площади под кривой распределения сами являются вероятностями. Отсюда, естественно, можно заключить, что вся площадь, ограниченная кривой распределения и осью абсцисс, равна единице, поскольку во всех случаях общая накопленная вероятность равна единице.
В
общем случае функцию
можно представить себе как суммарную
(общую) вероятность появления случайных
значений вплоть до
![]() ,
а функцию
–
как предельную вероятность значения
,
а функцию
–
как предельную вероятность значения
 .
.
Считают, что случайная величина задана теоретическим законом, если заданы её интегральная функция или её плотность вероятности .
Законы распределения дают полную, исчерпывающую характеристику об изучаемой случайной величине. Но для практических приложений часто нет необходимости описывать случайную величину полностью, исследуя функции и или ряд распределения. Бывает вполне достаточно знать только существенные черты, так называемые числовые характеристики (или моменты) распределения: математическое ожидание (среднее значение), дисперсию, среднеквадратическое отклонение и коэффициент вариации.
Перечисленные
числовые характеристики могут быть
двух родов теоретические и эмпирические.
Первые иногда называют параметрами
распределения случайных величин, вторые
- выборочными или статистическими
оценками этих параметров. Параметры
распределений – это обычно детерминированные
величины, в то время как выборочные
оценки – величины случайные. Причём,
разница между величиной параметра
распределения и его оценкой тем меньше,
чем большее число наблюдений
![]() используется
при проведении анализа. Характеристики
распределений (в виде оценок) используются
в статистической трактовке для обработки
результатов наблюдений и в вероятностной
трактовке (в виде параметров) для
прогнозирования надёжности.
используется
при проведении анализа. Характеристики
распределений (в виде оценок) используются
в статистической трактовке для обработки
результатов наблюдений и в вероятностной
трактовке (в виде параметров) для
прогнозирования надёжности.
Математическое
ожидание (среднее значение)
 –
основная и простейшая характеристика
случайной величины. Основные свойства
математического ожидания:
–
основная и простейшая характеристика
случайной величины. Основные свойства
математического ожидания:
математическое ожидание постоянной равно этой постоянной;
постоянный множитель можно вынести из под знака математического ожидания;
математическое ожидание суммы случайных величин равно сумме их математических ожиданий.
В
вероятностных задачах математическое
ожидание определяют в зависимости от
плотности распределения
(для непрерывной случайной величины)
или вероятности
 появления значений
(для дискретных случайных величин):
появления значений
(для дискретных случайных величин):

Величина
оценки математического ожидания или
среднее значение
![]() определяется
для непрерывных случайных величин, как
определяется
для непрерывных случайных величин, как
 ,
,
а для дискретных случайных величин
 ,
,
где
 - общее число наблюдений;
- общее число наблюдений;
 текущее значение случайной величины;
текущее значение случайной величины;
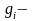 общее
число одинаковых (повторяющихся) значений
случайной величины.
общее
число одинаковых (повторяющихся) значений
случайной величины.
Среднее
значение
характеризует
центр группирования значений случайной
величины. При достаточно большом
количестве наблюдений (испытаний)
( )
выборочное значение
)
выборочное значение
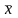 стремится по величине к математическому
ожиданию
стремится по величине к математическому
ожиданию

Иногда
в расчётах используют и другие
характеристики центра группирования
случайных величин. Мода
 дискретной случайной величины – это
наиболее вероятное значение этой
величины; для непрерывной величины мода
– это координата (абсцисса) максимума
кривой распределения
,
как показано на рис. 2.4.
дискретной случайной величины – это
наиболее вероятное значение этой
величины; для непрерывной величины мода
– это координата (абсцисса) максимума
кривой распределения
,
как показано на рис. 2.4.
Медиана
 характеризует
расположение центра группирования
случайной величины. Площадь под графиком
функции плотности распределения
делится медианой пополам. поэтому
математически – медиана это квантиль,
соответствующая вероятности 0,5.
характеризует
расположение центра группирования
случайной величины. Площадь под графиком
функции плотности распределения
делится медианой пополам. поэтому
математически – медиана это квантиль,
соответствующая вероятности 0,5.
Если кривая распределения симметрична, то математическое ожидание, мода и медиана совпадают; в противном случае они различны (см. рис.2.4).
Р ис.
2.4. Несимметричная кривая распределения.
Значения случайных величин, соответствующих
моде, медиане и математическому ожиданию
функции распределения
ис.
2.4. Несимметричная кривая распределения.
Значения случайных величин, соответствующих
моде, медиане и математическому ожиданию
функции распределения
Для
того чтобы охарактеризовать рассеяние
случайной величины относительно
математического ожидания или среднего
значения, вводится специальная
характеристика – дисперсия
 .
.
Дисперсией называется математическое ожидание квадрата разности случайной величины и её математического ожидания.
В соответствии с данным определением дисперсия непрерывной случайной величины вычисляется как
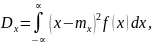
а для расчёта дисперсии дискретной случайной величины используют соотношение

Оценка величины дисперсии случайной величины – среднее значение квадрата разности между значениями случайной величины и её средним значением
 .
.
Дисперсия
имеет размерность квадрата случайной
величины. Так как удобнее пользоваться
характеристиками рассеяния, имеющими
ту же размерность, что и случайная
величина, то была введена характеристика
– среднеквадратическое отклонение
случайной величины
 ,
представляющее собой корень квадратный
из дисперсии, т.е.
,
представляющее собой корень квадратный
из дисперсии, т.е.
 или
или
 .
.
Для оценки степени рассеяния случайной величины с помощью безразмерной (относительной) величины используют коэффициент вариации, численно равный отношению среднеквадратического отклонения к математическому ожиданию или среднему значению случайной величины.
 .
.
Коэффициент вариации показывает насколько велико рассеяние по сравнению со средним значением случайной величины. При статистическом анализе выборочных данных наглядную информацию о характеристиках выборки анализируемой случайной величины можно получить, построив эмпирическую функцию распределения и гистограмму.
Эмпирическая
функция распределения
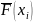 определяет для каждого значения случайной
величины
определяет для каждого значения случайной
величины
 частость (статистическую вероятность)
события, заключающегося в том, что
случайная величина
частость (статистическую вероятность)
события, заключающегося в том, что
случайная величина
 примет значение, меньшее
примет значение, меньшее

где
общее число наблюдений (объём выборки);
 накопленная частота, т.е. число вариант
со значениями, меньшими
.
накопленная частота, т.е. число вариант
со значениями, меньшими
.
Для интервального вариационного ряда эмпирическая функция распределения имеет вид ступенчатой кривой. Ширина каждой ступеньки соответствует длине интервала разбиения, а высота – соответствует значению накопленной частоты.
Гистограмма служит графическим представлением интервального статистического ряда случайных величин. Её построение является методом, с помощью которого можно понять генеральную совокупность с первого взгляда.
Строится гистограмма по следующим правилам:
Размах значений вариационного ряда (разность между крайними значениями наблюдаемой случайной величины) разбивается на ряд интервалов;
Над каждым интервалом строятся прямоугольники высотой

где
 количество членов выборки, попавших в
данный интервал;
количество членов выборки, попавших в
данный интервал;
 длина интервала.
длина интервала.
Построенную гистограмму называют гистограммой относительных частот. Площадь гистограммы относительных частот равна сумме всех относительных частот интервалов, т.е. единице.
ТЕМА 3
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ
НАДЁЖНОСТИ ТЕХНИЧЕСКИХ УСТРОЙСТВ
И ТЯГОВОГО ПОДВИЖНОГО СОСТАВА
Машины, их агрегаты и узлы, приборы и целые системы принято называть одним термином – объект (изделие). Объект состоит из элементов, т.е составных частей, неделимых в условиях эксплуатации.
В настоящее время существуют два возможных подхода к оценке надёжности машин массового производства: функциональный и вероятностно-статистический.
При использовании функционального подхода о надёжности технической системы судят по величине показателя, определяющего её техническое состояние (например, по величине коэффициента полезного действия, величине мощности двигателя, величине удельного расхода топлива или энергии и т.п.). Выход такого показателя за допустимые пределы означает недопустимое падение надёжности.
Успехи этого развивающегося подхода связаны с развитием и широким внедрением в практику нового направления – без разборной диагностики технических систем. При развитии средств автоматизации считывания данных и их анализа можно будет давать заключение о состоянии узла или даже целой системы быстро и без её разборки. Кроме этого, функциональный подход позволяет дать заключение о надёжности каждого конкретного образца технической системы.
При вероятностно-статистическом подходе оценивается надёжность не конкретного изделия, а данной модели (группы) изделий. Вероятностно-статистический подход учитывает, что в условиях массового производства размеры, масса, геометрические и физико-технические параметры изделий могут меняться в определённых пределах, возможны их не благоприятные сочетания и скрытые дефекты даже у новых образцов продукции. Если такие изделия производятся серийно или крупными партиями, то в условиях эксплуатации появляется возможность достаточно быстро собрать необходимый статистический материал, характеризующий их надёжность. Типичным в этом смысле объектом является подвижной состав железных дорог.
Локомотив подобен человеку – у каждого своя судьба. Несмотря на высокую стабильность производства, качество новых локомотивов, а тем более прошедших капитальный ремонт, существенно различаются. Среда, в которой работают однотипные локомотивы (прежде всего, состояние верхнего строения пути и климатические факторы), условия эксплуатации (прежде всего, скорости движения, нагрузки, качество технического обслуживания) различны. Поэтому показатели локомотивов, в частности, характеризующие их надёжность, являются случайными функциями (для каждого конкретного локомотива в любой момент времени рассчитать их в точности нельзя). Приходится прибегать к вероятностно-статистическим оценкам, лежащим в основе теории надёжности, которые и будут предметом дальнейшего рассмотрения.
В будущем можно ожидать комбинированного подхода к оценке надёжности локомотивов. Данные автоматизированной оценки функционального состояния конкретного образца будут сочетаться с прогнозированием характера изменения его показателей надёжности, уже с использованием вероятностной оценки показателей работы совокупности локомотивов определённой серии.
Основные понятия и определения теории надёжности технических устройств сформулированы в ГОСТ «Надёжность в технике. Термины и определения». В соответствии с этим стандартом надёжность – это свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортирования.
На базе этого ГОСТа разработан и утверждён ОСТ 32. 46 – 95. «Тяговый подвижной состав железнодорожного транспорта. Надёжность. Термины и определения».
Указанные документы устанавливают три основных термина, относящиеся как к отдельным узлам, так и к локомотиву в целом: свойство, состояние и событие.
Свойство локомотива выполнять тяговые функции, сохраняя свои параметры в установленных пределах в течение заданного времени, является его надёжностью. Надёжность – это сложное свойство, слагающееся из более простых свойств: безотказности, ремонтопригодности, долговечности и сохраняемости.
Безотказность – свойство локомотива сохранять работоспособность в течение заданного времени без вынужденных перерывов на ремонт. В свою очередь, понятие работоспособность определяется как состояние локомотива, при котором он способен выполнять заданные функции, сохраняя значения основных параметров в пределах, установленных нормативно-технической документацией.
Отказы локомотива устраняют в процессе проведения ремонтов, восстанавливая его работоспособность. Следовательно, только свойство безотказности не полностью характеризует надёжность восстанавливаемых систем или узлов. Поэтому вводят понятие свойства ремонтопригодности.
Под ремонтопригодностью понимают приспособленность узла, детали или системы к обнаружению и устранению отказов путём проведения технического обслуживания и выполнения ремонта.
Долговечность – способность узла, детали или локомотива сохранять свою работоспособность до предельного состояния с необходимыми перерывами на ремонт. Предельное состояние локомотива – это такое состояние, при котором дальнейшее его использование по назначению должно быть прекращено из-за неустранимого нарушения требований безопасности, неустранимого отклонения заданных параметров за установленные пределы, недопустимого увеличения эксплуатационных расходов или необходимости проведения капитального ремонта. Момент достижения предельного состояния определяется физическим либо моральным износом. Физический износ наступает в том случае, когда дальнейший ремонт и эксплуатация локомотива становятся невыгодными, так как затраты на содержание локомотива начинают превышать доход, получаемый от его использования по назначению. Моральный износ наступает тогда, когда основные технические параметры локомотива перестают отвечать современным требованиям.
Сохраняемостью – называют свойство локомотива непрерывно сохранять своё исправное и работоспособное состояние в течение установленного времени транспортирования или нахождения в резерве.
В зависимости от вида и назначения объекта его надёжность может определяться всеми или только частью перечисленных свойств. Так, например, для локомотива наиболее важными свойствами являются – безотказность, ремонтопригодность и долговечность. А для ракеты стратегического назначения – главными свойствами являются сохраняемость и безотказность.
Состояния, в которых может находиться локомотив, достаточно разнообразны. Локомотив может быть: работоспособным, неработоспособным, исправным, работоспособным и неисправным, не работоспособным и неисправным.
При исправном состоянии локомотив соответствует всем требованиям Правил технической эксплуатации (ПТЭ). При нарушении хотя бы одного из требований ПТЭ – локомотив переходит в неисправное состояние.
Стук коренного подшипника дизеля или перегоревшая лампа на пульте управления локомотива – это неисправности. Однако, разница в значении этих двух неисправностей огромна: локомотив с отказавшей сигнальной лампой сохраняет все свои основные свойства (объект продолжает функционировать); выход из строя дизеля – это выход из строя локомотива. Таким образом, в первом случае локомотив неисправен, но работоспособен. Во втором случае и неисправен, и неработоспособен.
Событие – это переход локомотива из одного возможного состояния в другое. Примерами событий являются отказы и повреждения. Отказом называют нарушение работоспособного состояния, в результате чего локомотив полностью или частично теряет свои тяговые свойства. повреждение – это событие, заключающееся в нарушении исправного состояния.
Таким образом, от широкого понятия исправность – неисправность (повреждение) объекта переходят к более узкому определению: работоспособность – отказ.
Следовательно, сгоревшая сигнальная лампочка – это повреждение, а выплавление вкладыша коренного подшипника дизеля – это отказ.
Предметом дальнейшего рассмотрения будут не повреждения, а отказы и условия сохранения работоспособности локомотивов.
ТЕМА 4