24. Предел функции
Определение
предела по Коши. Число A называется пределом
функции f (x) в точке a, если
эта функция определена в некоторой
окрестности точки a за исключением,
быть может, самой точки a, и для каждого
ε > 0 существует δ > 0 такое,
что для всех x, удовлетворяющих
условию|x – a| < δ, x ≠ a,
выполняется неравенство |f (x) – A| < ε.
Если A – предел функции в точке a,
то пишут, что
Эквивалентность двух определений предела функции
Теорема
1. Первое и
второе определения предела функции в
точке прикосновения множества определения
функции эквивалентны.
Доказательство.
Докажем, что если функция имеет в
некоторой точке предел по Гейне, то она
имеет тот же самый предел в этой точке
и по Коши. Пусть
, x0 – точка прикосновения множества X
и в смысле первого определения предела
функции.
Ограничимся здесь случаем конечных x0 и a. Допустим, что предел по Коши не совпадает с пределом по Гейне, т. е.
. (12.1)
Возьмём
. Выберем в каждой такой d-окрестности
точки x0 элемент xn. Тогда, по построению,
имеем последовательность .
При этом, в силу (4), все элементы
последовательности
лежат
вне e-окрестности точки a.
С
другой стороны, поскольку
в
смысле первого опр-ия, то для любой
последовательности
имеет
место равенство
.
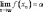Согласно определению предела
последовательности это означает, что
для любой окрестности точки a, в частности
и для выбранной выше e-окрестности,
существует такой номер N, что для всех
номеров n>N имеет место
Полученное
противоречие доказывает сделанное
утверждение. Теперь докажем, что если
функция имеет в некоторой точке предел
в смысле второго определения, то она
имеет в этой точке тот же самый предел
и в смысле первого определения. Пусть
в
смысле предела функции по Коши
,
, x0 – предельная точка множества X, и
пусть
.
Покажем, что тогда
,
т. е. точка a является пределом функции
f и в смысле определения предела функции
по Гейне.
Зададим произвольную e-окрестность точки a. Тогда, по условию теоремы,
.
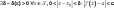
(12.2)Для этой d-окрестности найдётся
такой номер N, что для всех номеров n>N
будет выполняться условие
.
Но тогда, в
силу (5), имеем
.
Это и означает, что
.
Если
же x0 – изолированная точка множества
X, то функция f непрерывна в этой точке
(почему?) и имеет место равенство .
Основными задачами и темами изучения математического анализа являются: рассмотрение элементов теории множеств, вещественных чисел, понятий функции и ее графика, изучение пределов последовательности и функции, непрерывности функции
26. Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Во
всех приведённых ниже формулах
бесконечность справа от равенства
подразумевается определённого знака
(либо «плюс», либо «минус»). То есть,
например, функция xsin x, неограниченная
с обеих сторон, не является бесконечно
большой при
.
Последовательность
an называется бесконечно большой, если
.
Функция
называется бесконечно большой в
окрестности точки x0, если
Функция
называется бесконечно большой на
бесконечности, если
либо
.
Связь бесконечно малой и бесконечно большой величины
Величина, обратная бесконечно малой величине, есть величина бесконечно большая, и наоборот, величина, обратная бесконечно большой величине, есть величина бесконечно малая.
Пусть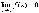 
и 
,
тогда 
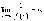и 
.
Символически можно записать:
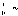и 
Свойства б.б
Пусть 
и 
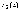бесконечно
большие величины при 
,
т.е. 
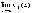и 
.
1. Сумма бесконечно больших величин есть величина бесконечно большая:
.
(4.20)
2.
Произведение бесконечно больших величин
есть величина бесконечно большая:
.
(4.21)
3.
Произведение бесконечно большой
величины на константу С,
или на функцию, имеющую конечный предел
,
есть величина бесконечно большая:
(4.22)