22. Числовая последовательность.

Если каждому числу n из натурального ряда чисел: 1, 2, 3, …, n, … поставлено в соответствие вещественное число xn, то множество вещественных чисел x1, x2, …,xn, … называется числовой последовательностью или просто последовательностью. последовательность содержит бесконечное число элементов, любые два ее элемента отличаются, по крайней мере, своими номерами. Арифметические действия над числовыми последовательностями

Пусть даны последовательности {xn} и {yn}.

Произведением последовательности {хn} на число m назовем последовательность m·x1, m·x2, …, m·xn, ….

Суммой данных последовательностей назовем последовательность x1 + y1, x2 + y2, …, xn + yn, ….

Разностью – последовательность x1 − y1, x2− y2, …, xn− yn, …,

Произведением — последовательность x1·y1, x2·y2, … xn·yn,…

Частным — последовательность если все члены последовательности {yn} отличны от нуля.

m·{ xn} = {m· xn}

– { xn} + { yn} = { xn + yn}

– { xn} - { yn} = { xn - yn}

– { xn} · { yn} = { xn · yn}

– если yn ≠ 0.

Ограниченные и неограниченные последовательности

Числовая последовательность {хn} назыв. ограниченной, если существуют числа m и M, такие, что любой элемент xn этой последовательности удовлетворяет неравенствам m ≤ xn ≤ M. Пусть А = max{

| m |, | M |}. Тогда условие ограниченност. последовательн. можно записать в виде | xn | ≤ А n ≥ N:

Здесь и в дальнейшем будем пользоваться квантором всеобщности и квантором существования . Не вдаваясь в подробности определения этих логических операций, будем читать квантором всеобщности как "для любого", а квантор существования как "существует". Последовательность {хn} называется неограниченной, если для любого как угодно большого положительного числа А существует элемент xn этой последовательности, удовлетворяющий неравенству | xn | > A, (т.е. либо xn > A, либо xn < - A):

Последовател. ограничена сверху, если все ее элементы принадлежат промежутку ( - ∞, M]:

Последовател. ограничена снизу, если все ее эл-ты принадлеж промежутку [m, + ∞):

З а м е ч а н и е. Неограниченная последовател. может быть ограничена сверху (снизу). Сравнивая запись с помощью логических символов двух последних определений, видим, что при построении отрицаний символы и заменяют друг друга и неравенства меняют свой смысл.

Бесконечно большие и бесконечно малые последовательности

Определение. Последовательность { хn} называется бесконечно большой, если для как угодно большого любого положительн. числа А существует номер N, зависящий от этого числа А, такой, что для всех последующих номеров n > N выполняется неравенство | xn | > A:

Замечание. Очевидно, что любая бесконечно большая последовательность является неограниченной. Однако неограниченная последовательность может и не быть бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3, …, 1, n + 1, … не является бесконечно большой, поскольку при A > 1 неравенство | xn| > A выполняется не для всех элементов xn с нечетными номерами.

Определение. Последовательность {αn} называется бесконечно малой, если для любого как угодно малого положительного числа ε > 0 существует номер N, зависящий от этого ε, такой, что для любых n > N выполняется неравенство |αn| < ε:

20. Множества

Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.Множества обозначаются заглавными буквами латинского алфавита , а элементы множества- строчными.

   - заменяет выражение "для любого",

 - «существует»,

^! - читается «существует единственный».

25.Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю. Последовательность an называется бесконечно малой, если . Например, последовательность чисел 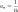— бесконечно малая.Функция называется бесконечно малой в окрестности точки x0, если Функция называется бесконечно малой на бесконечности, если 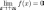либо .Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если , то f(x) − a = α(x), .

Свойства бесконечно малых

Сумма конечного числа бесконечно малых — бесконечно малая. Произведение бесконечно малых — бесконечно малая.

Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

Если an — бесконечно малая послед-ность, сохраняющая знак, то — бесконечно большая послед-ность.

Функция называется  ограниченной, если существует такое положительное число M, что |  f ( x ) |    M  для всех значений  x . Если такого числа не существует, то функция - неограниченная.

Функция, изображённая на рис.3, является ограниченной, но не монотонной. Функция на рис.4 - как раз наоборот, монотонная, но неограниченная.