23. Предел последовательности

Определение. Если каждому натуральному числу ставится в соответствие некоторое вещественное число , то множество вещественных чисел  называется последовательностью.  Определение. Число называется пределом последовательности , если для любого положительного числа существует натуральное число такое, что при всех выполняется неравенство .

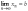Если последовательность имеет предел , то говорят, что она сходится к числу , и записывают при , или , или

В противном случае говорят, что последовательность расходится. 

Монотонные последовательности

Определение. Последовательность   называется неубывающей (невозрастающей) ,  если    справедливо неравенство .

Если на самом деле выполняются строгие неравенства  , то последовательность   называется строго возрастающей (строго убывающей) или просто возрастающей (убывающей). Последовательности убывающие и возрастающие, неубывающие и невозрастающие называются монотонными.

Элементы монотонных последовательностей можно расположить в цепочки 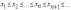     , откуда видно, что неубывающая последовательность ограничена снизу, а невозрастающая сверху.

Число е Рассмотрим последовательность

.

Покажем, что эта последовательность возрастающая и ограничена сверху. На основании формулы бинома Ньютона

имеем

                   (1)

Из данного равенства видно, что последовательность  . Докажем, что последовательность   ограничена сверху. Из равенства (1) имеем

.

Покажем, что последовательность   возрастающая. По аналогии с (1) имеем

             (2)

Сравнивая (1) и (2), видим, что   (в (2) каждое слагаемое больше, чем соответствующее слагаемое в (1), и, кроме того, имеется на одно положительное слагаемое больше). По теореме 1 § 2.5 последовательность   сходится. Обозначим ее предел буквой  ,  как это предложил впервые Л. Эйлер

.

Из сказанного ясно, что  . Более точное значение

.

Теорема Больцано – Вейерштрасса.

Пусть задана произвольная последовательность действительных чисел   . Выберем из нее бесконечное множество элементов с номерами  . Тогда получим новую последовательность  , которая называется подпоследовательностью последовательности  . Таких подпоследовательностей можно выделить из данной последовательности бесконечное множество.

Если последовательность   сходится (к конечному числу, 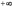  или  ), то очевидно, что и любая ее подпоследовательность тоже сходится и притом к тому же числу (конечному,   или   ).

Теорема  1. Из всякой последовательности действительных чисел   можно выделить подпоследовательность , сходящуюся к конечному числу, или к  , или к  .

В случае, когда последовательность   не ограничена сверху (снизу), она, очевидно, содержит в себе подпоследовательность, стремящуюся к   (к  ), что доказывает теорему. Если же последовательность ограничена, то теорема 1 сводится к следующей теореме.

Теорема 2 (Больцано-Вейерштрасса). Из всякой ограниченной последовательности   можно выделить подпоследовательность  , сходящуюся к некоторому числу.