3.Понятие вектора.

Направленные отрезки принято называть также геометрическими векторами или просто векторами. Векторы называются равными, если они имеют одинаковые длины, лежат на параллельных прямых или на одной прямой и направлены в одну сторону. Число, равное длине вектора (при заданном масштабе), называется его модулем. Модуль вектора a обозначается символом или а. Если, то вектор называется единичным.

Линейные операции над векторами и их св-ва: Сложение векторов коммутативно: A+b=b+a, Сложение векторов ассоциативно: a+b)+c=a+(b+c), Умножение вектора на число ассоциативно:λ(µa)=(λµ)a, Умножение вектора на число дистрибутивно относительно сложения чисел: (λ+µ)a=λa+µa, умножение вектора на число дистрибутивно относительно сложения векторов: λ(a+b)= λa+λb

Прибавление нулевого вектора к любому не меняет последнего:  . Очевидно, .

Для любого вектора   существует вектор такой, что или . умножение на единицу не меняет вектор:  .

Коммутативность и Ассоциативность

сложения векторов

Дистрибутивность умножения векторов относительно сложения

7 Векторное произведение векторов

Вектор называется векторным произведением неколлинеарных векторов a и b , если:

1) его длина равна произведению длин векторов a и b на синус угла между ними:

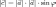
2) вектор c ортогонален векторам a и b ;

3) векторы (в указанном порядке) образуют правую тройку. Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.

Векторное произведение обозначается 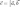(или ).

Свойства.

Для любых векторов и любого действительного числа :

1. ;

2. ;

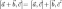3. .

6 Скалярное произведение векторов.Свойства.

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.

Обозначается ab,а* b(или( а, b)).Итак, по определению,

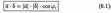
1) a ×b = |a|2;

2) a× b= 0, если a ^b или a = 0 или b = 0.

3) a×b =b ×a;

4) a×(b+c) =a ×b+ a×c;

5) (ma)×b = a×(mb) = m(×ab); m=const

5 Базис и координаты вектора.

Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Базисом называется совокупность отличных от нулей линейно независимых векторов.

базисом на плоскости являются любые два неколлинеарных вектора на этой плоскости.

базисом в пространстве назовём три некомпланарных вектора.

Координатами (или компонентами) вектора a в базисе называются коэффициенты разложения вектора a по векторам базиса. ля указания, что вектор a имеет координаты , мы будем использовать запись . Очевидно, что в фиксированном базисе каждый вектор имеет свой, единственный, набор координат. Если же взять другой базис, то координаты вектора в общем случае изменятся.

При умножении вектора на число все его координаты умножаются на это число. При сложении векторов складываются их соответствующие координаты.

Таким образом, любой вектор в декартовой прямоугольной системе координат можно записать в виде: .

Ортом называется вектор единичной длины.

Теорема3) Если вектор умножается на число λ, то его проекция на ось также умножается на это число:

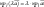
8 Cмешанное произведение векторов. Свойства

Смешанным произведением трех векторов   называется число

Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на этих векторах.

Пусть   правая тройка векторов (рис. 9). Действительно, объем параллелепипеда, построенного на векторах  , равен площади основания   на высоту . Здесь φ - угол между векторами  и 

1)Смешанное произведение кососимметрично по отношению ко всем своим аргументам:

т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что

2)Смешанное произведение в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов a,b и c :

3)Смешанное произведение в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и , взятому со знаком "минус":

4) Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.

5)Геометрический смысл — Смешанное произведение по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами и знак зависит от того, является ли эта тройка векторов правой или левой.

4.Понятие проекции вектора.

Свойства(3 теоремы)

Проекцией вектора на ось u называется число, равное величине отрезка оси u, где точка является проекцией точки А на ось u, а - проекцией точки В на эту ось. Проекция вектора на ось u выражается через его модуль и угол наклона к оси u формулой

Теорема1) Проеция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью:

Теорема2) Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось: .

17. Эллипс

Определение. Эллипс есть геометрическое место точек, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (большая, чем расстояние между фокусами).

Внешний вид уравнения какого-либо геометрического места точек зависит от взаимного расположения этого множества точек и декартовой системы координат.

Выберем прямоугольную систему декартовых координат так, чтобы ось абсцисс проходила через оба фокуса F1 и F2, начало координат находится в середине отрезка F1F2 (рис. 7). Если обозначить расстояние между фокусами F1 и F2 через 2с, тогда координаты фокусов будут соответственно (-с, 0) и (с, 0).

Пусть М(х, у) - текущая точка эллипса (рис. 7).

Обозначим сумму расстояний

F1M и F2M через 2а (a > c по правилу треугольника), т.е.  , или

Уравнение (36) и есть уравнение эллипса. Приведем его к более простой для исследований форме:

Поскольку a > c, то можно обозначить

тогда получаем

Окончательно получим (при выбранной системе координат) уравнение

Уравнение (38) называют каноническим уравнением эллипса.

Сделаем некоторые замечания о форме эллипса. Из уравнения (38) понятно, что оси координат Ох и Оу являются осями симметрии эллипса и, следовательно, начало координат является центром симметрии эллипса.

Рассмотрим часть эллипса, расположенную в первой четверти, для которой можем записать уравнение (38) в виде:

Отсюда видно, что если x = 0, то y = b и, далее, с ростом х значения у убывают. Когда x = a, то y = 0 (рис. 8).

Числа а и b называют полуосями эллипса.

Учитывая симметрию эллипса относительно осей координат, можем построить полный эллипс (рис. 9).

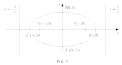
Если изменяется величина с, то меняется форма эллипса, а именно: если   и при c = 0 эллипс становится окружностью с уравнением 

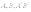Т.о., окружность есть частный случай эллипса, когда полуоси эллипса равны между собой. Если же   , то  , т.е. эллипс сжимается вдоль оси Оу.  Величина   может служить числовой характеристикой сжатия эллипса.  Число   называют эксцентриситетом эллипса.  Две прямые   называются директрисами эллипса.  Точки пересечения эллипса с осями симметрии   называют вершинами эллипса.

Директрисы гиперболы параллельны оси Оу и пересекают ось Ох между вершинами гиперболы.

18 Гипербола.ривая плоскость эллипс Определение. Гипербола есть геометрическое место точек, абсолютное значение разности расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (не равная нулю и меньшая, чем расстояние между фокусами).

Расстояние между фокусами F1 и F1 обозначим 2c. Систему координат выберем так же, как при выводе уравнения эллипса (рис. 10).

Из определения имеем

следовательно, a > c. Опуская вывод, запишем уравнение гиперболы

где b2 =c2- a2.

Уравнение (40) называют каноническим уравнением гиперболы. Число а называют действительной полуосью гиперболы, число b - мнимой полуосью.

Отметим, что согласно уравнению (40) гипербола симметрична относительно осей координат и, следовательно, относительно начала координат. Т.к. из канонического уравнения гиперболы следует, что

то нет точек кривой в полосе -a > x > a.

Кривая состоит из двух отдельных частей - ветвей гиперболы, лежащих в областях   (рис. 10).

Можно показать, что при   ветви гиперболы неограниченно приближаются к прямым  , не пересекая этих прямых.

Эти две прямые называются асимптотами гиперболы (рис. 10).  Число  , количественно характеризующее сжатие ветвей гиперболы, называют эксцентриситетом гиперболы. 

Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки гиперболы до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету гиперболы: . Точки пересечения гиперболы с действительной осью называются вершинами гиперболы.  Две прямые  называют директрисами гиперболы.