19 Парабола
Выберем систему координат так, чтобы ось абсцисс проходила через точку фокуса F перпендикулярно директрисе L, начало координат расположим в середине отрезка FN (рис. 11).
Расстояние между фокусом F и директрисой L обозначим р. Значение р называют параметром параболы.
Пусть
M(x, y) - текущая точка параболы, тогда, по
определению параболы имеем 
или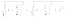 
отсюда
получаем
Уравнение (41) называют каноническим уравнением параболы.
Уравнение
(1) называется каноническим уравнением
параболы. В этой же системе координат
директриса данной параболы имеет
уравнение
Фокальный
радиус произвольной точки М(x; y) параболы
(то есть длина отрезка F(M) может быть
вычислен по формуле
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.
Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат - с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид
(2)
В
случае, когда начало координат находится
в вершине, а с осью совмещена ось ординат,
парабола будет иметь уравнение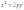
(3)
; если она лежит в верхней полуплоскости
(рис.), и
(4)
если в нижней полуплоскости (рис.)
Вершина параболы находится в начале координат, и кривая симметрична относительно оси Ох (рис. 11).
Замечание. Если для эллипса и гиперболы обозначим через r расстояние от текущей точки кривой до какого-либо фокуса, а через d - расстояние от этой точки до односторонней с этим фокусом директрисы, то оказывается, что
Для параболы же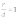 
,
что следует из ее определения.
Т.о., для рассмотренных кривых второго порядка эллипса, гиперболы, параболы имеет место фокально-директориальное свойство: отношение расстояния текущей точки кривой до фокуса к расстоянию до односторонней с этим фокусом директрисы равно эксцентриситету кривой, т.е.
21.Понятие функции. Способы задания функции
Определение. Переменная величина y называется функцией переменной x (обозначается ), если каждому значению x соответствует определенное значение - число y.
Функция считается заданной (известной), если для каждого значения аргумента (из числа возможных) можно узнать соответствующее её значение. Функция может быть задана различными способами.
1. Табличный способ задания функции заключается в составлении таблицы:
x |
x1 |
x2 |
x3 |
x4 |
|
y |
x1 |
y2 |
y3 |
y4 |
|
в которой заданным значениям независимой переменной x ставятся в соответствие определенные значения функции y.
2. Графический. Функция задается в виде графика (рис. 2).
3. Аналитический способ. Функция задается в виде формулы, например:
Классификация функций:
рассмотрим однозначные и многозначные. Если каждому значению аргумента соответствует одно значение функции, то она называется однозначной; если два или больше, - то многозначной (двузначной, трехзначной и т. д.). Когда особо не оговорено, что она многозначна, подразумевается, что - однозначна.
Также те, которые представленные формулами, подразделяются на явные и неявные
Ещё бывают элементарные и неэлементарные. Последнее носит скорее исторический, чем математический характер. Каждая из основных элементарных функций представляет некоторое «действие» над аргументом (возведение в квадрат, извлечение кубического корня, логарифмирование, нахождение синуса и т. д.). Путем повторного выполнения этих действий, а также четырех основных операций арифметики (в ограниченном числе) получаются новые; они также причисляются к элементарным. Те, которые нельзя выразить указанным способом, считаются неэлементарными. И на конец, они могут быть алгебраические и трансцендентные.
